Algorithm for determining whether a point hits a contour based on a comprehensive analysis
Hello to all Habra people. I want to present an example to dear readers when the higher mathematics, which is dry and far from life in our understanding, gave not a bad practical result.

It was when my student was one of the technical universities in the 90s, probably the second course. I somehow got to the programming contest. And at this very Olympiad there was a task: to set the coordinates of a triangle, a test point on a plane, and to determine whether this point belongs to a triangle area. In general, a trifling problem, but then I did not solve it. But after thinking about a more general task - belonging to the landfill. I repeat - it was the mid-90s, there was no Internet, there were no books on computer geometry, and there were lectures on the tower and a laboratory of 286-s with turbo pascal. And so the stars so coincided that just at the time when I was pondering over the problem, we read the theory of a complex variable in the tower. And one formula (about it below) fell on fertile soil. The algorithm was invented and implemented on Pascal (unfortunately my one and a half gig screw died and took this code and a bunch of my other youthful experiences into oblivion). After graduation, I got to work in one research institute. There I had to develop a GIS for the needs of the institute’s employees and one of my tasks was to determine whether objects entered the contour. The algorithm was rewritten in C ++ and has proven itself to work.
')
The derivation of formulas for the subsequent writing of the algorithm in no way pretends to mathematical completeness and accuracy, but only demonstrates an engineering (consumer approach) to the Queen of thefields of science.
So, let's begin

Explanation from aworker-peasant engineering point of view:
- boundary our given contour,
- z0-tested point
- f (z) - a complex function of a complex argument does not go anywhere in the contour to infinity.
That is, to establish the membership of a point in a contour, we need to calculate the integral and compare it with the value of the function at the given point. If they match, then the point lies in the contour. Note: the integral Cauchy theorem says that if a point does not lie in a contour, those integrand does not go to infinity anywhere, then the integral is zero. This simplifies the matter - you just need to calculate the integral and check it for equality to zero: the point is not a contour point, different - lies in the contour.
Let us calculate the integral. For f (z), we take a simple function 1. Without breaking the generality, we can take the point 0 for z0 (we can always move the coordinates).

We get rid of the imaginary unit in the denominator of the integrand and split the integral into real and imaginary parts:

It turned out two curvilinear integrals of the second kind.
Calculate the first
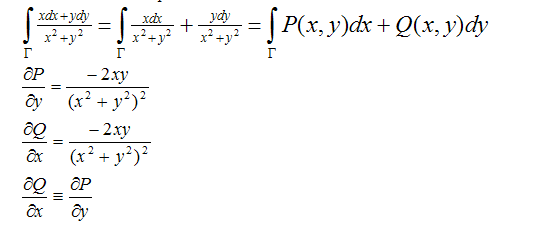
The condition that the integral does not depend on the path is satisfied, therefore, the first integral is zero and it is not necessary to calculate it.
With the imaginary part of this focus does not pass. Remember that our border consists of straight line segments, we get:

Where gi is a segment (xi, yi) - (xi + 1, y i + 1)
Calculate the i-th integral. To do this, we write the equation of the i-th segment in parametric form

Substitute the integral
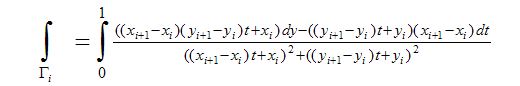
and after cumbersome and tedious transformations, we obtain the following seductive formula:
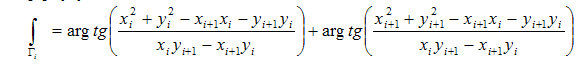
Finally we get
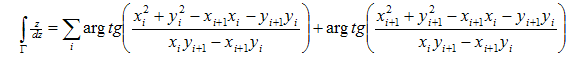

First some memories
It was when my student was one of the technical universities in the 90s, probably the second course. I somehow got to the programming contest. And at this very Olympiad there was a task: to set the coordinates of a triangle, a test point on a plane, and to determine whether this point belongs to a triangle area. In general, a trifling problem, but then I did not solve it. But after thinking about a more general task - belonging to the landfill. I repeat - it was the mid-90s, there was no Internet, there were no books on computer geometry, and there were lectures on the tower and a laboratory of 286-s with turbo pascal. And so the stars so coincided that just at the time when I was pondering over the problem, we read the theory of a complex variable in the tower. And one formula (about it below) fell on fertile soil. The algorithm was invented and implemented on Pascal (unfortunately my one and a half gig screw died and took this code and a bunch of my other youthful experiences into oblivion). After graduation, I got to work in one research institute. There I had to develop a GIS for the needs of the institute’s employees and one of my tasks was to determine whether objects entered the contour. The algorithm was rewritten in C ++ and has proven itself to work.
Task for the algorithm
')
Given:
G - closed polyline (hereinafter referred to as a polygon) on a plane, given by the coordinates of its vertices (xi, yi), and the coordinate of the test point (x0, y0)Define:
Does a point belong to a region D bounded by a polygon?The derivation of formulas for the subsequent writing of the algorithm in no way pretends to mathematical completeness and accuracy, but only demonstrates an engineering (consumer approach) to the Queen of the
So, let's begin
Cauchy Integral Formula

Explanation from a
- boundary our given contour,
- z0-tested point
- f (z) - a complex function of a complex argument does not go anywhere in the contour to infinity.
That is, to establish the membership of a point in a contour, we need to calculate the integral and compare it with the value of the function at the given point. If they match, then the point lies in the contour. Note: the integral Cauchy theorem says that if a point does not lie in a contour, those integrand does not go to infinity anywhere, then the integral is zero. This simplifies the matter - you just need to calculate the integral and check it for equality to zero: the point is not a contour point, different - lies in the contour.
Let us calculate the integral. For f (z), we take a simple function 1. Without breaking the generality, we can take the point 0 for z0 (we can always move the coordinates).

We get rid of the imaginary unit in the denominator of the integrand and split the integral into real and imaginary parts:

It turned out two curvilinear integrals of the second kind.
Calculate the first
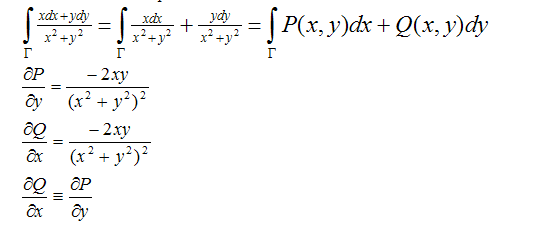
The condition that the integral does not depend on the path is satisfied, therefore, the first integral is zero and it is not necessary to calculate it.
With the imaginary part of this focus does not pass. Remember that our border consists of straight line segments, we get:

Where gi is a segment (xi, yi) - (xi + 1, y i + 1)
Calculate the i-th integral. To do this, we write the equation of the i-th segment in parametric form

Substitute the integral
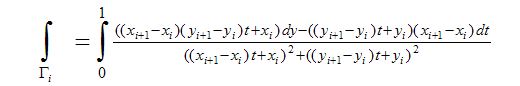
and after cumbersome and tedious transformations, we obtain the following seductive formula:
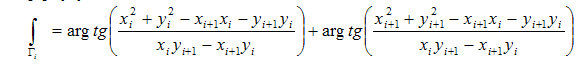
Finally we get
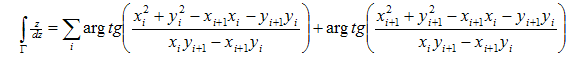
Algorithm in C ++:
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
template < class T>
bool pt_in_polygon( const T &test,const std::vector &polygon)
{
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T last_pt=polygon.back();
last_pt.x-=test.x;
last_pt.y-=test.y;
double sum=0.0;
for (
std::vector::const_iterator iter=polygon.begin();
iter!=end;
++iter
)
{
T cur_pt=*iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
double del= last_pt.x*cur_pt.y-cur_pt.x*last_pt.y;
double xy= cur_pt.x*last_pt.x+cur_pt.y*last_pt.y;
sum+=
(
atan((last_pt.x*last_pt.x+last_pt.y*last_pt.y - xy)/del)+
atan((cur_pt.x*cur_pt.x+cur_pt.y*cur_pt.y- xy )/del)
);
last_pt=cur_pt;
}
return fabs(sum)>eps;
}
T – , :
struct PointD
{
double x,y;
};
2D : Anti-Grain Geometry (AGG) .
:
–
-
Shift- –
PS
, , . .
forgotten .
template bool pt_in_polygon2(const T &test,const std::vector &polygon)
{
static const int q_patt[2][2]= { {0,1}, {3,2} };
if (polygon.size()<3) return false;
std::vector::const_iterator end=polygon.end();
T pred_pt=polygon.back();
pred_pt.x-=test.x;
pred_pt.y-=test.y;
int pred_q=q_patt[pred_pt.y<0][pred_pt.x<0];
int w=0;
for(std::vector::const_iterator iter=polygon.begin();iter!=end;++iter)
{
T cur_pt = *iter;
cur_pt.x-=test.x;
cur_pt.y-=test.y;
int q=q_patt[cur_pt.y<0][cur_pt.x<0];
switch (q-pred_q)
{
case -3:++w;break;
case 3:--w;break;
case -2:if(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x) ++w;break;
case 2:if(!(pred_pt.x*cur_pt.y>=pred_pt.y*cur_pt.x)) --w;break;
}
pred_pt = cur_pt;
pred_q = q;
}
return w!=0;
}
Source: https://habr.com/ru/post/125356/
All Articles