The distribution of the number of moves in the card game 'Drunkard'
While playing this wonderful game, I noticed that my brain was completely turned off. the game does not require mental activity, respectively, I was bored. I was looking forward to when this game is over and decided to estimate approximately how many more moves needed? Without a computer, of course, it did not work out, and then I decided that it was necessary to conduct several hundreds of thousands of tests, count the mat. waiting, dispersion and, if possible, find out the type of distribution. Armed with ++, qt and a cup of coffee, I got down to business ...
A deck of cards is carefully peretosovyvaetsya and distributed equally to two players (18 cards). Players simultaneously draw the top card and from whom it is higher - it takes both, while the six is considered higher than the ace. In the event that the cards are equal, both players pull out one more card (if there is one) and put them in a closed one, and then pull them out in the open one more and compare them, who has more - takes everything, and if they are equal, the dispute resolution another iteration is performed.
It is important that the cards from the table get under the bottom of the deck and at the same time also shuffled (to eliminate the possibility of cycles).
')
During the implementation of the program, I tried to abstract away from the cards as much as possible, called the cards from six to ace with numbers from 0 to 8, completely ignored suits. The test result strongly depends on the quality of the distribution - on how random the cards in the decks of players are). However, even a thorough rewrite does not guarantee an absolute chance, so I didn’t invent anything in the program, but just swapped randomly selected cards from the deck a thousand times:
The algorithm is that both players, while everyone has cards, repeat the iteration of the game, which is that as long as someone has cards on hand and there are conflicts (both cards are equal; the turn has not yet been made), the players whenever possible, 1-2 cards are thrown off and, evaluating their face value, decide who gets all the cards thrown on the table ...
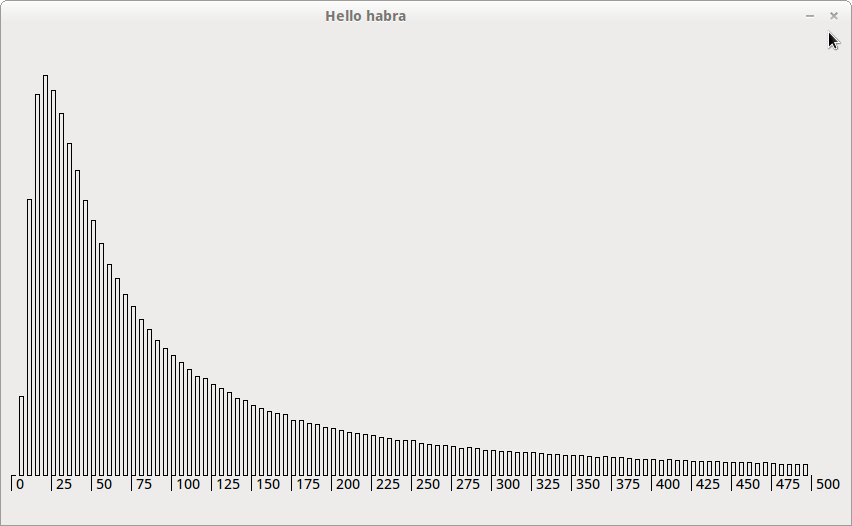
The graph shows the probability distribution of a random variable of the number of moves needed to complete the game.
For 100 seconds, my E8400 in one stream spent 1,000,000 tests. The schedule surprised me a lot, it turns out that most often the games end in 25 moves. And sometimes less ... But seeing the results of the calculation of the mat. expectations and variance, I calmed down, everything is fine:
Math waiting: Mx = 255.054;
Dispersion: Dx = 319726.545;
Total, judging by the mat. waiting, if you take to play this game - count on 30 minutes. And judging by the variance, if you take on playing this game - do not even think about counting on something).
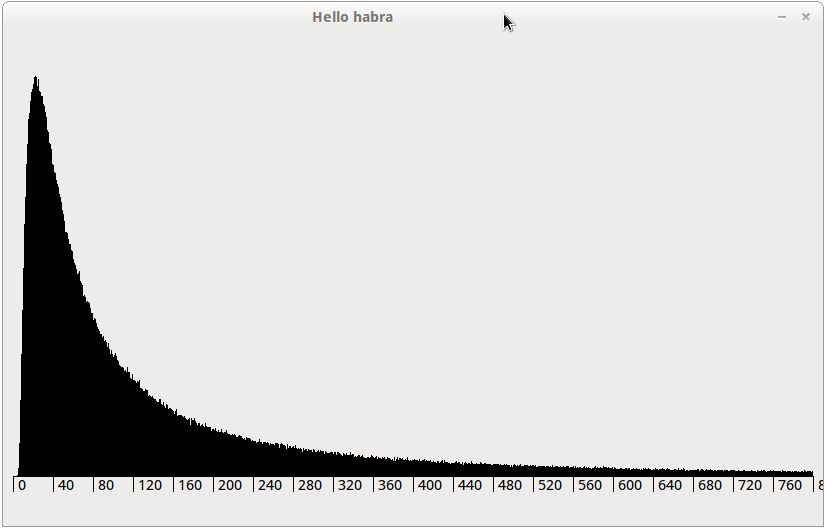
Slightly more detailed density graph.
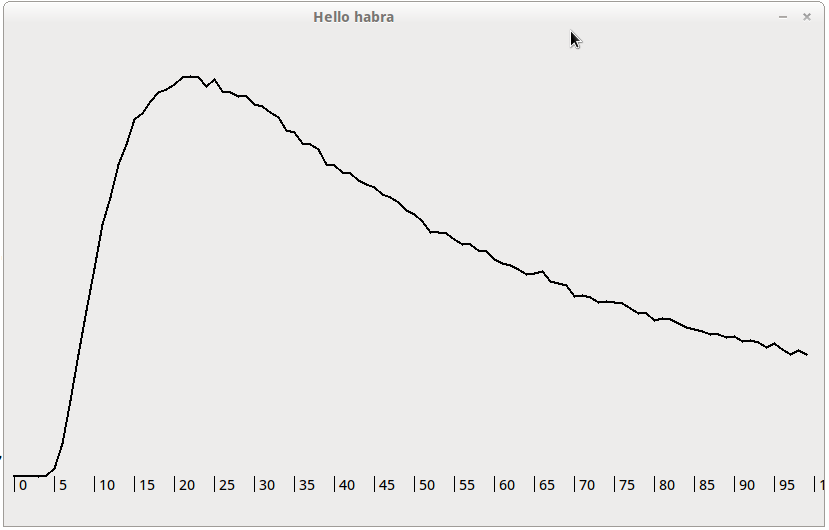
"Increases" of the "main part".

LN (f) at the request of OLS
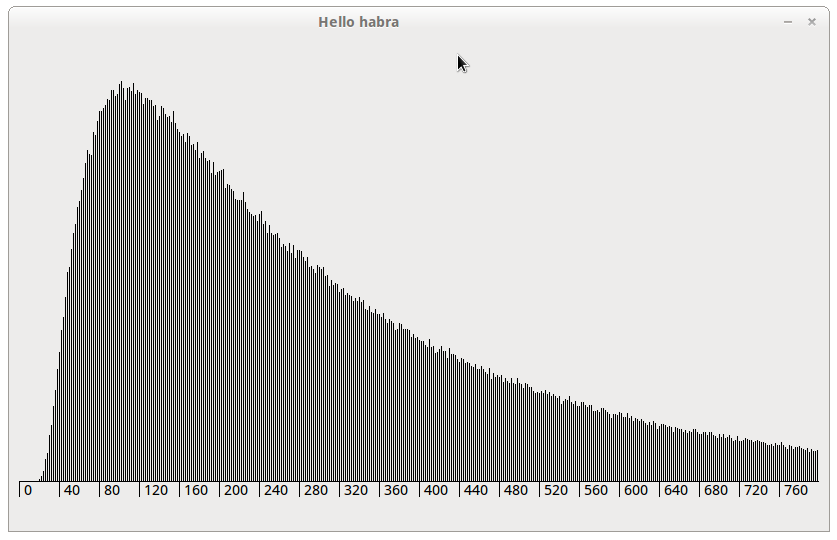
For the continuous version of the game (maps - numbers from 0..1), the difference is only in the distribution parameters and that f (x) = 0 for all unpaired x. Made at the request of Bodigrim
A few more properties:
Median: 90;
Fashion: 25;
Confidence interval: 80% - from 6 to 316.
I apologize, several annoying errors were found in the code, which greatly distort the result. This update is re-checked n times, you can check the correctness of the tests here , here and here .

The final result:
Mat. waiting: 187 ;
Dispersion: 23044 ;
Median: 142 ;
Fashion: 62 .
On the graph you can see2 independent graphs that the pair numbers have a greater frequency. This can be explained by the fact that no matter how many (1, 3, 5 ...), who and when picks up the cards, the number c1 + c2 is a pair.
c1 is the number of moves made.
c2 is the number of cards for any of the players (each has a pair of cards or an unpaired number of cards at the same time).
One and only one situation leads the game to a close with an unpaired number of moves - when one of the players selects a pair of cards, which ends the game. This can only happen at the end of the game, an example .
Once again, I apologize; for pointing out errors, thanks to Catalysis
Rules of the game
A deck of cards is carefully peretosovyvaetsya and distributed equally to two players (18 cards). Players simultaneously draw the top card and from whom it is higher - it takes both, while the six is considered higher than the ace. In the event that the cards are equal, both players pull out one more card (if there is one) and put them in a closed one, and then pull them out in the open one more and compare them, who has more - takes everything, and if they are equal, the dispute resolution another iteration is performed.
It is important that the cards from the table get under the bottom of the deck and at the same time also shuffled (to eliminate the possibility of cycles).
')
Distribution of cards
During the implementation of the program, I tried to abstract away from the cards as much as possible, called the cards from six to ace with numbers from 0 to 8, completely ignored suits. The test result strongly depends on the quality of the distribution - on how random the cards in the decks of players are). However, even a thorough rewrite does not guarantee an absolute chance, so I didn’t invent anything in the program, but just swapped randomly selected cards from the deck a thousand times:
void generateMap(QList* player1, QList* player2)
{
int a[36];
for ( int i = 0; i < 36; i++)
a[i] = i / 4;
int temp, i1, i2;
for ( int i = 0; i < 1000; i++)
{
i1 = random() % 36;
i2 = random() % 36;
temp = a[i1];
a[i1] = a[i2];
a[i2] = temp;
}
for ( int i = 0; i < 18; i++)
{
player1->append(a[i]);
player2->append(a[i+18]);
}
}
Game process
The algorithm is that both players, while everyone has cards, repeat the iteration of the game, which is that as long as someone has cards on hand and there are conflicts (both cards are equal; the turn has not yet been made), the players whenever possible, 1-2 cards are thrown off and, evaluating their face value, decide who gets all the cards thrown on the table ...
int Process(QList* player1, QList* player2)
{
QList* temp = new QList();
int p1, p2, k;
int counter = 0;
while ((player1->count() > 0) && (player2->count() > 0))
{
p1 = -1; p2 = -1;
while ((p1 == p2) && ((player1->count() > 0) || (player2->count() > 0)))
{
for ( int i = 0; i < 1 + (p1 >= 0); i++)
if (player1->count() > 0) {
p1 = player1->first();
temp->append(p1);
player1->removeFirst();
}
for ( int i = 0; i < 1 + (p2 >= 0); i++)
if (player2->count() > 0) {
p2 = player2->first();
temp->append(player2->first());
player2->removeFirst();
}
}
QList* winner;
if ((p1 > p2) || ((p1 == 0) && (p2 == 8))) {
winner = player1;
} else {
winner = player2;
}
while (!temp->isEmpty())
{
k = random() % temp->count();
winner->append(temp->at(k));
temp->removeAt(k);
}
temp->clear(); counter++;
if (counter > 100000) player1->clear();
}
delete temp;
return counter;
}
Result Display

The graph shows the probability distribution of a random variable of the number of moves needed to complete the game.
void CChart::paintEvent(QPaintEvent *){
QPainter painter( this );
for ( int i = 0; i < 21; i++) {
painter.drawText(QRect(i*40+15,450,30,20),QString::number(i*25));
painter.drawLine(10+i*40, 465, 10+i*40,450);
}
for ( int i = 0; i < 100; i++){
int h = this ->counts[i] * 400 / this ->max;
painter.drawRect(10 + i*8, 450-h, 4, h);
}
}
findings
For 100 seconds, my E8400 in one stream spent 1,000,000 tests. The schedule surprised me a lot, it turns out that most often the games end in 25 moves. And sometimes less ... But seeing the results of the calculation of the mat. expectations and variance, I calmed down, everything is fine:
Math waiting: Mx = 255.054;
Dispersion: Dx = 319726.545;
Total, judging by the mat. waiting, if you take to play this game - count on 30 minutes. And judging by the variance, if you take on playing this game - do not even think about counting on something).
Update

Slightly more detailed density graph.

"Increases" of the "main part".

LN (f) at the request of OLS

For the continuous version of the game (maps - numbers from 0..1), the difference is only in the distribution parameters and that f (x) = 0 for all unpaired x. Made at the request of Bodigrim
A few more properties:
Median: 90;
Fashion: 25;
Confidence interval: 80% - from 6 to 316.
Update 2
I apologize, several annoying errors were found in the code, which greatly distort the result. This update is re-checked n times, you can check the correctness of the tests here , here and here .

The final result:
Mat. waiting: 187 ;
Dispersion: 23044 ;
Median: 142 ;
Fashion: 62 .
On the graph you can see
c1 is the number of moves made.
c2 is the number of cards for any of the players (each has a pair of cards or an unpaired number of cards at the same time).
One and only one situation leads the game to a close with an unpaired number of moves - when one of the players selects a pair of cards, which ends the game. This can only happen at the end of the game, an example .
Once again, I apologize; for pointing out errors, thanks to Catalysis
Source: https://habr.com/ru/post/124881/
All Articles