Optimization in compilers. Part 1
Delving into the wilds of LLVM , I suddenly found out for myself: how interesting the thing is - code optimization. Therefore, I decided to share with you my observations in the form of a series of review articles about optimization in compilers. In these articles, I will try to “chew on” the principles of optimization work and be sure to consider examples.
I will try to build optimization in order of increasing "complexity of understanding", but this is purely subjective.
And one more thing: some names and terms are not well-established and are used by “someone-like”, therefore I will give several options, but I strongly recommend using English terms.
Before we dive into great ideas and algorithms, let's be a little bored with theory: let's look at what optimization is, what it is for, and what they are or are not.
To begin with, we will give a definition ( from wikipedia ):
Go ahead: optimizations are machine-independent (high-level) and machine-dependent (low-level) . The meaning of the classification is clear from the names; in machine-dependent optimizations, features of specific architectures are used; in high-level optimizations, this occurs at the level of the code structure.
Depending on their area of application, optimizations can also be classified into local ones (operator, operator sequence, base unit), intraprocedural, interprocedural, intramodular and global (optimization of the whole program, “optimization during assembly”, “Link-time optimization” ).
')
I feel that you are going to fall asleep now, let's finish this portion of the theoiai and begin to consider the optimizations themselves ...
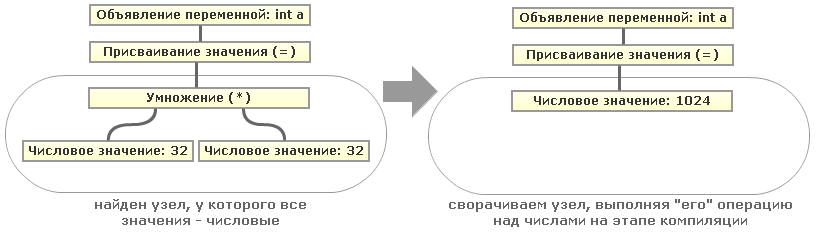
The simplest, most famous and most common optimization in compilers. The process of "folding constants" includes the search for expressions (or subexpressions) that include ONLY constants. Such expressions are calculated at the compilation stage and are “collapsed” into the calculated value in the resulting code.
Consider an example ( invented on the move from the head, absolutely synthetic, trivial, abstract, meaningless, far from reality, etc ... and all the examples will be like this):
It seems to be fine and the optimization is done, but in fact the compilers have become smarter and move on. The fact is that in this case the size (
Well ... A few processor cycles this optimization definitely saves us.
It's pretty simple, if our code is presented as an Abstract Syntax Tree ( AST ). Then, to find numerical expressions and subexpressions, it suffices to search for tree nodes of the same level (that is, having a common ancestor) containing only numerical values. Then the value in the parent node (parent) can be minimized. For clarity, consider a simple example of a tree for one of the expressions, take our
That is, by recursively traversing our AST tree, we can collapse all such constant expressions. By the way, the example with numbers is again simplified; instead of operations with numbers, there may well be operations with strings (concatenation) or operations with strings and numbers (similar to python's "
This optimization is usually always described in a set with “Constant folding” (after all, they complement each other), but this is still a separate optimization. The process of “propagation of constants” includes in the search for expressions that will be constant in any possible way of execution (before using this expression) and replacing them with these values. In fact, everything is simpler than it sounds - let's take the same example that we have already used, but given that we have already gone through it with the optimization of “Constant folding” :
That is, in our initial program, in general, it was not necessary to do any calculations. What happened? Everything is simple ... Since the values of the variables
That is, it is necessary for the compiler to check for each expression whether its value will always be constant (or rather, whether it can change). Let's try to sketch:
Suppose that the compiler detects the use of the variables
"Constant propagation" and "Constant folding" are usually run several times until they stop making any changes to the program code.
And this is another companion of the two previous optimizations, practically twin brother “Constant Folding”, performing very similar work, but it allows you to get rid of unnecessary (intermediate) variable assignments, replacing intermediate variables in expressions. It will be much clearer on the simplest example:
Very simple, but, unfortunately, there is little that improves the performance optimization in terms of performance. Everything is simple: the code that can not be used in the program can be deleted. Let's look at a couple of examples of “dead codeload ”:
As you can see, the line "
I think everything here is also clear without comments: the line "
Well, the last example for this optimization:
And again, everything is simple: the sub function is not called in any place in the program, so you can get rid of it.
On the one hand, the “dead code” in the program is very easy to find using the control flow graph . If the program has a dead code, then the graph will either be disconnected and you can “throw away” some fragments of the graph. On the other hand, it is necessary to take into account address arithmetic and many other nuances - it is not always possible to determine unambiguously whether the code is “dead”.
Very useful and “beautiful” optimization. It consists in the following: if you use the calculation of an expression two or more times, then it can be calculated once, and then substituted into all expressions using it. Well, where are we without an example:
Yes, this optimized code looks much worse and more cumbersome, but it is free from “extra calculations” (adding and subtracting x and y once instead of triple, multiplying a and b once twice together). Now imagine how much this optimization saves CPU time in a large computing program.
PS In fact, I wanted to bring the schematics for each of the optimizations, but excuse me, I only had enough to draw two.
PPS Prompt CONVENIENT service for drawing sherik and graphs.
PPPS To be continued?
I will try to build optimization in order of increasing "complexity of understanding", but this is purely subjective.
And one more thing: some names and terms are not well-established and are used by “someone-like”, therefore I will give several options, but I strongly recommend using English terms.
Introduction
(very little theory about the types of optimizations you can skip)
Before we dive into great ideas and algorithms, let's be a little bored with theory: let's look at what optimization is, what it is for, and what they are or are not.
To begin with, we will give a definition ( from wikipedia ):
Optimization of program code is a modification of programs performed by an optimizing compiler or interpreter in order to improve their characteristics, such as performance or compactness, without changing the functionality.The last three words in this definition are very important: no matter how much the optimization optimizes the characteristics of the program, it must preserve the original meaning of the program under any conditions. That is why, for example, there are various levels of optimization in GCC (I strongly recommend to go through these links) .
Go ahead: optimizations are machine-independent (high-level) and machine-dependent (low-level) . The meaning of the classification is clear from the names; in machine-dependent optimizations, features of specific architectures are used; in high-level optimizations, this occurs at the level of the code structure.
Depending on their area of application, optimizations can also be classified into local ones (operator, operator sequence, base unit), intraprocedural, interprocedural, intramodular and global (optimization of the whole program, “optimization during assembly”, “Link-time optimization” ).
')
I feel that you are going to fall asleep now, let's finish this portion of the theoiai and begin to consider the optimizations themselves ...
Constant folding
(Coagulation / Constant Convolution)
The simplest, most famous and most common optimization in compilers. The process of "folding constants" includes the search for expressions (or subexpressions) that include ONLY constants. Such expressions are calculated at the compilation stage and are “collapsed” into the calculated value in the resulting code.
Consider an example ( invented on the move from the head, absolutely synthetic, trivial, abstract, meaningless, far from reality, etc ... and all the examples will be like this):
| Before optimization | After optimization |
|---|---|
| |
sizeof ) of the "p" structure is also a constant, and the compilers know about it, so we get:| Expand sizeof | End the collapse |
|---|---|
| |
It's pretty simple, if our code is presented as an Abstract Syntax Tree ( AST ). Then, to find numerical expressions and subexpressions, it suffices to search for tree nodes of the same level (that is, having a common ancestor) containing only numerical values. Then the value in the parent node (parent) can be minimized. For clarity, consider a simple example of a tree for one of the expressions, take our
"int a = 32*32;" :That is, by recursively traversing our AST tree, we can collapse all such constant expressions. By the way, the example with numbers is again simplified; instead of operations with numbers, there may well be operations with strings (concatenation) or operations with strings and numbers (similar to python's "
'-' * 10 ") or constants of any other data types supported by the source language programming.Constant propagation
(Spreading constants)
This optimization is usually always described in a set with “Constant folding” (after all, they complement each other), but this is still a separate optimization. The process of “propagation of constants” includes in the search for expressions that will be constant in any possible way of execution (before using this expression) and replacing them with these values. In fact, everything is simpler than it sounds - let's take the same example that we have already used, but given that we have already gone through it with the optimization of “Constant folding” :
| Before optimization | After optimization |
|---|---|
| |
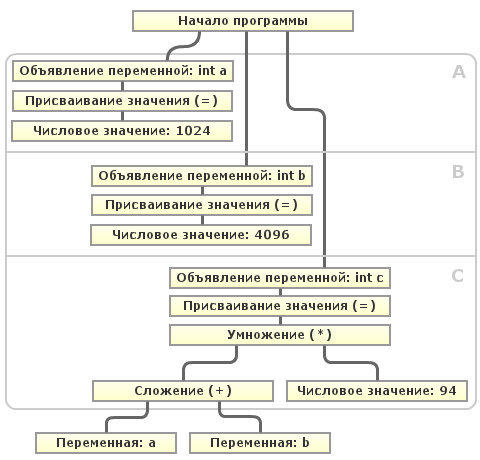
"a" and "b" in no way change between their declaration and the use of the value "c" in the calculation, the compiler itself can substitute their values into the expression and calculate it.That is, it is necessary for the compiler to check for each expression whether its value will always be constant (or rather, whether it can change). Let's try to sketch:
Suppose that the compiler detects the use of the variables
"a" and "b" during the next optimization pass. As can be seen from the diagram, after declaring the variable "a" in block A and the variable "b" in block B, neither one nor the other variable can change the value in subsequent blocks (A, B, C) before using them. This case is trivial, since the whole program is linear and is the so-called Base unit ( BB ) . But the algorithm for determining the "variability" of a variable in the base unit is far from all. The program may include conditional constructions, cycles, unconditional transitions, etc. Then, to determine the “variability” of a variable, it is necessary to construct a directed graph with base blocks at the vertices, and edges — transfer of control between the base blocks. Such a graph is called a Control Flow Graph ( CFG ) and is used to implement many optimizations. In this box, you can determine all the basic blocks that need to go from initializing the variable to its use and determine for each block whether the variable value can change in it. If it cannot be changed, the compiler can easily replace its value with a constant."Constant propagation" and "Constant folding" are usually run several times until they stop making any changes to the program code.
Copy propagation
(Distribution of copies)
And this is another companion of the two previous optimizations, practically twin brother “Constant Folding”, performing very similar work, but it allows you to get rid of unnecessary (intermediate) variable assignments, replacing intermediate variables in expressions. It will be much clearer on the simplest example:
| Before optimization | After optimization |
|---|---|
| |
Dead Code Elimination (DCE)
(Elimination / Exclusion of unavailable code)
Very simple, but, unfortunately, there is little that improves the performance optimization in terms of performance. Everything is simple: the code that can not be used in the program can be deleted. Let's look at a couple of examples of “dead code
| Before optimization | After optimization |
|---|---|
| |
printf("Hi, I'm dead code =( !"); " Is unreachable under any circumstances: either the program runs infinitely or ends "forcibly." Let's give a couple more examples:| Before optimization | After optimization |
|---|---|
| |
printf("x = %d \n", &x); " also, as in the previous example, is unreachable in any way of program execution, and the variable declared in the first line of the function main is y not used.Well, the last example for this optimization:
| Before optimization | After optimization |
|---|---|
| |
On the one hand, the “dead code” in the program is very easy to find using the control flow graph . If the program has a dead code, then the graph will either be disconnected and you can “throw away” some fragments of the graph. On the other hand, it is necessary to take into account address arithmetic and many other nuances - it is not always possible to determine unambiguously whether the code is “dead”.
Common Sub-Expression Elimination (CSE)
(Elimination of common subexpressions)
Very useful and “beautiful” optimization. It consists in the following: if you use the calculation of an expression two or more times, then it can be calculated once, and then substituted into all expressions using it. Well, where are we without an example:
| Before optimization | After optimization |
|---|---|
| |
PS In fact, I wanted to bring the schematics for each of the optimizations, but excuse me, I only had enough to draw two.
PPS Prompt CONVENIENT service for drawing sherik and graphs.
PPPS To be continued?
Source: https://habr.com/ru/post/124131/
All Articles