Estimation of the number of errors in the program. Double evaluation, Historical experience
Continuing to post model mills .
This model requires testing by two specialists (or groups of specialists). But does not require the introduction of artificial errors in the program. So, let the program be tested independently by two groups of specialists. Suppose that the program contains N errors. Let the first group found N 1 errors, and the second - N 2 . Part of the errors detected by both groups. Let such errors N 12 .

')
The effectiveness of the work of the groups will be estimated through the percentage of errors found by them:
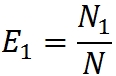
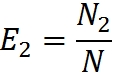
We believe that all errors are equally probable (which, in my opinion, reduces the credibility of this model, as is the case with Mills). Then, due to the equal probability of finding any of the errors, any randomly selected subset of N can be considered as an approximation of the entire set N. This means that if the first group found 10% of all errors, it should detect approximately 10% of any randomly selected subset .
For such a randomly selected subset, take the set of errors found by the second group. The proportion of all errors found by the first group is N 1 / N. The proportion of errors found by the first group among the errors that were found by the second group is N 12 / N 2 . According to this reasoning, these two quantities should be equal:
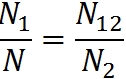
Hence the number of errors in the program:

The number of errors found is (NN 1 -N 2 + N 12 ).
For example, let the first group find 8 errors, the second 9. Both groups found 3 errors. Then the number of errors in the program is N = (8 * 9/3) = 24. From them it is already found (8 + 9-3) = 14. Therefore it remains to find 10 pieces.
This model appeared in the process of working on OS / 360 by IBM. The following formula was used to estimate the number of errors: N = 2 * IM + 23 * MIM. Here
N is the total number of bug fixes,
IM - the number of modules to be fixed,
MIM - the number of repeatedly corrected modules.
Modules that were repeatedly repaired were considered modules that required 10 or more patches. MI was estimated at 90% of new modules and 15% of old ones. MIM - like 15% new and 6% old. When substituting such estimates in the formula, we obtain the form:
N pat = 2 * (0.9 * N new mod. + 0.15 * N old mod. ) + 23 * (0.15 * N new mod. + 0.06 * N old mod. )
Thus, if there are 140 modules in the system, and another 20 are to be added to the update process, the number of errors, which will be detected at the same time, is estimated as follows:
2 * (0.9 * 20 + 0.15 * 140) + 21 * (0.15 * 20 + 0.06 * 140) = 2 * (18 + 21) + 23 * (3 + 8.4) = 78 + 262.2 = 340.2
You can expect 340 errors. In 18 out of 20 new modules, at least one correction will have to be made, in 3 modules - at least a dozen. Of the old modules, at least once it is necessary to correct 21 modules, and 8 or 9 modules - at least 10 times.
It should be borne in mind that this model was developed for a specific system. Not the fact that it can be directly applied in other cases.
When writing the article, the manual "Testing and debugging for dummies and not only for them" was used (M.A. Plaksin)
Pair assessment
This model requires testing by two specialists (or groups of specialists). But does not require the introduction of artificial errors in the program. So, let the program be tested independently by two groups of specialists. Suppose that the program contains N errors. Let the first group found N 1 errors, and the second - N 2 . Part of the errors detected by both groups. Let such errors N 12 .

')
The effectiveness of the work of the groups will be estimated through the percentage of errors found by them:
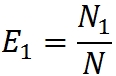
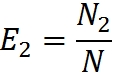
We believe that all errors are equally probable (which, in my opinion, reduces the credibility of this model, as is the case with Mills). Then, due to the equal probability of finding any of the errors, any randomly selected subset of N can be considered as an approximation of the entire set N. This means that if the first group found 10% of all errors, it should detect approximately 10% of any randomly selected subset .
For such a randomly selected subset, take the set of errors found by the second group. The proportion of all errors found by the first group is N 1 / N. The proportion of errors found by the first group among the errors that were found by the second group is N 12 / N 2 . According to this reasoning, these two quantities should be equal:
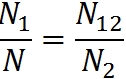
Hence the number of errors in the program:

The number of errors found is (NN 1 -N 2 + N 12 ).
For example, let the first group find 8 errors, the second 9. Both groups found 3 errors. Then the number of errors in the program is N = (8 * 9/3) = 24. From them it is already found (8 + 9-3) = 14. Therefore it remains to find 10 pieces.
Historical experience
This model appeared in the process of working on OS / 360 by IBM. The following formula was used to estimate the number of errors: N = 2 * IM + 23 * MIM. Here
N is the total number of bug fixes,
IM - the number of modules to be fixed,
MIM - the number of repeatedly corrected modules.
Modules that were repeatedly repaired were considered modules that required 10 or more patches. MI was estimated at 90% of new modules and 15% of old ones. MIM - like 15% new and 6% old. When substituting such estimates in the formula, we obtain the form:
N pat = 2 * (0.9 * N new mod. + 0.15 * N old mod. ) + 23 * (0.15 * N new mod. + 0.06 * N old mod. )
Thus, if there are 140 modules in the system, and another 20 are to be added to the update process, the number of errors, which will be detected at the same time, is estimated as follows:
2 * (0.9 * 20 + 0.15 * 140) + 21 * (0.15 * 20 + 0.06 * 140) = 2 * (18 + 21) + 23 * (3 + 8.4) = 78 + 262.2 = 340.2
You can expect 340 errors. In 18 out of 20 new modules, at least one correction will have to be made, in 3 modules - at least a dozen. Of the old modules, at least once it is necessary to correct 21 modules, and 8 or 9 modules - at least 10 times.
It should be borne in mind that this model was developed for a specific system. Not the fact that it can be directly applied in other cases.
When writing the article, the manual "Testing and debugging for dummies and not only for them" was used (M.A. Plaksin)
Source: https://habr.com/ru/post/123473/
All Articles