Estimation of the number of errors in the program. Model Mills
How many bugs in the program? This is a question that worries every programmer. Of particular relevance is the principle of the bumpiness of errors , according to which an error in a module increases the probability that there are other errors in this module. It is often impossible to give an exact answer to the question about the number of errors in the program, but it is possible to build some estimate. To do this, there are several static models. Consider one of these: the Mills Model.
In 1972, the super programmer at IBM, Harlan Mills, proposed the following method for estimating the number of errors in a program. Suppose we have a program. Suppose that there are N errors in it. Let's call them natural . We add to it additionally M artificial errors. We will test the program. Suppose that during the test, n natural errors and m artificial errors were found. Suppose that the probability of detection for natural and artificial errors is the same. Then the relation is satisfied:
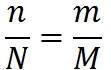
')
We found the same percentage of natural and man-made errors. Hence the number of errors in the program:

The number of undetected errors is (Nn).
For example, suppose that 20 artificial errors were introduced into the program, during the testing 12 artificial and 7 natural errors were discovered. We get the following estimate of the number of errors in the program:

The number of undetected errors is (Nn) = 12 - 7 = 5.
It is easy to see that in the Mills method described above there is one major drawback. If we find 100% artificial errors, it will mean that we found 100% of natural errors. But the less artificial errors we make, the more likely we are to find them all. We make the only artificial error, find it, and on this basis we will declare that we have found all the natural errors! To solve this problem, Mills added the second part of the model, designed to test the hypothesis about the value of N:
Suppose that the program N natural errors. Fill it with M artificial errors. We will test the program until we find all the artificial errors. Let n natural errors be found by this moment. Based on these numbers, we calculate the value of C :
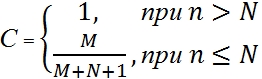
The value of C expresses a measure of confidence in the model. This is the probability that the model will correctly reject the false assumption. For example, suppose we assume that there are no natural errors in the program (N = 0). Let's add 4 artificial errors to the program. We will test the program until we find all the artificial errors. Let us not detect a single natural error with this. In this case, the measure of confidence in our assumption (about the absence of errors in the program) will be equal to 80% (4 / (4 + 0 + 1)). In order to bring it to 90%, the number of artificial errors will have to be raised to 9. The next 5% of confidence in the absence of natural errors will cost us 10 additional artificial errors. M will have to bring to 19.
If we assume that in the program no more than 3 natural errors (N = 3), we add 6 artificial (M = 6) into it, we find all artificial and one, two or three (but not more!) Natural errors, then the measure trust in the model will be 60% (6 / (6 + 3 + 1)).
The values of the function C for different values of N and M, in percent:
Table 1 - in steps of 1;
Table 2 - in increments of 5;
From the formulas for calculating the confidence measure, it is easy to obtain a formula for calculating the number of artificial errors that need to be made to the program to obtain the necessary confidence in the resulting estimate:

The number of artificial errors that must be made to the program, in order to achieve the desired confidence level, for different values of N:
Table 3 - with step 1;
Table 4 - in increments of 5;
Model Mills is quite simple. Her weak point is the assumption of equal probability of finding errors. In order for this assumption to be justified, the procedure for making artificial errors must have a certain degree of “intelligence”. Another weak point is the requirement of the second part of the Mills model to find all the artificial errors. And this may not happen for a long time, maybe never.
In 1972, the super programmer at IBM, Harlan Mills, proposed the following method for estimating the number of errors in a program. Suppose we have a program. Suppose that there are N errors in it. Let's call them natural . We add to it additionally M artificial errors. We will test the program. Suppose that during the test, n natural errors and m artificial errors were found. Suppose that the probability of detection for natural and artificial errors is the same. Then the relation is satisfied:
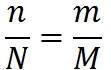
')
We found the same percentage of natural and man-made errors. Hence the number of errors in the program:

The number of undetected errors is (Nn).
For example, suppose that 20 artificial errors were introduced into the program, during the testing 12 artificial and 7 natural errors were discovered. We get the following estimate of the number of errors in the program:

The number of undetected errors is (Nn) = 12 - 7 = 5.
It is easy to see that in the Mills method described above there is one major drawback. If we find 100% artificial errors, it will mean that we found 100% of natural errors. But the less artificial errors we make, the more likely we are to find them all. We make the only artificial error, find it, and on this basis we will declare that we have found all the natural errors! To solve this problem, Mills added the second part of the model, designed to test the hypothesis about the value of N:
Suppose that the program N natural errors. Fill it with M artificial errors. We will test the program until we find all the artificial errors. Let n natural errors be found by this moment. Based on these numbers, we calculate the value of C :
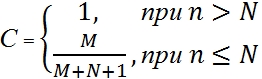
The value of C expresses a measure of confidence in the model. This is the probability that the model will correctly reject the false assumption. For example, suppose we assume that there are no natural errors in the program (N = 0). Let's add 4 artificial errors to the program. We will test the program until we find all the artificial errors. Let us not detect a single natural error with this. In this case, the measure of confidence in our assumption (about the absence of errors in the program) will be equal to 80% (4 / (4 + 0 + 1)). In order to bring it to 90%, the number of artificial errors will have to be raised to 9. The next 5% of confidence in the absence of natural errors will cost us 10 additional artificial errors. M will have to bring to 19.
If we assume that in the program no more than 3 natural errors (N = 3), we add 6 artificial (M = 6) into it, we find all artificial and one, two or three (but not more!) Natural errors, then the measure trust in the model will be 60% (6 / (6 + 3 + 1)).
The values of the function C for different values of N and M, in percent:
Table 1 - in steps of 1;
Table 2 - in increments of 5;
From the formulas for calculating the confidence measure, it is easy to obtain a formula for calculating the number of artificial errors that need to be made to the program to obtain the necessary confidence in the resulting estimate:

The number of artificial errors that must be made to the program, in order to achieve the desired confidence level, for different values of N:
Table 3 - with step 1;
Table 4 - in increments of 5;
Model Mills is quite simple. Her weak point is the assumption of equal probability of finding errors. In order for this assumption to be justified, the procedure for making artificial errors must have a certain degree of “intelligence”. Another weak point is the requirement of the second part of the Mills model to find all the artificial errors. And this may not happen for a long time, maybe never.
Source: https://habr.com/ru/post/122912/
All Articles