Number Theory in TeX-way

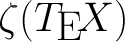We demonstrate some features of writing TeX macros by embedding a number-theoretic calculator into TeX.

Formulation of the problem

From time to time I have to type regular text, followed by examples of calculating number-theoretic functions: the Euler function φ , the divisor function τ , the Carmichael function λ . Previously, it was done this way: we launch our favorite calculator (my choice is PARI / GP ), we consider everything in it and copy the calculations in TeX. The original data has changed - again to the calculator and back. A lot of fuss, a lot of chances to forget to replace some intermediate result. And just waving a mouse bothers. I want to automate this process at least for the most common functions so that you can write

$\phi(1001)=\Phi(1001)$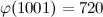 

and get on print


The most common solution is to use an external preprocessor that would bite the necessary fragments of the formulas, pass them on to the external calculator, take the result and insert it into the document. The main disadvantage is, of course, the loss of compatibility. Before, we could just send a tex file by email. Now, in order to be able to compile it into pdf at that end of the wire, we also need a detailed instruction indicating the necessary preprocessor and calculator. At this stage, we will almost certainly find out that the recipient has a different OS and our dances with a tambourine are not needed for him. Go to plan B.

Plan b

Let's try to do with TeX's own means, the macros of which, as we know, make up the Turing-complete language. It is not as esoteric as Brainfuck, but very far from C-like syntax and, worse, semantics.
')
The first thing to notice is that the macro can take arguments, but cannot return values ​​transparently. A pascalist would say that a macro behaves not as a function, but as a procedure. Here, for example, how you can write a macro that summarizes two numbers:

 \newcount\s\def\addition#1#2{\s=#1\advance\s by#2 \number\s} 

Confused? Let's try again, only with comments and spaces:

 \newcount\s %    \def\addition#1#2{ %      \s=#1 %   s   \advance\s by#2 %    \number\s %    } 

Now

 2+3=\addition{2}{3} 

will give the seal "2 + 3 = 5".

( A few more examples of mathematical functions )

Division completely

Let's write something more complicated. Our first goal is a function that checks whether one number divides to another without a remainder.

 \newif\ifdivisible %    \newcount\testMod@n %    \def\testMod#1#2{ %      \testMod@n=#1 %   testMod@n   \divide\testMod@n by#2 %      \multiply\testMod@n by#2 %      \ifnum#1=\testMod@n %       , \divisibletrue %    , \else %   \divisiblefalse %  \fi% } 

This macro places divisible truth, if the division has passed without a trace, and false otherwise. Checking:

 \testMod{6}{3} \ifdivisible 1 \else 0 \fi \testMod{6}{4} \ifdivisible 1 \else 0 \fi 

should give the output "1 0": 6 divided by 3, but not divided by 4.

If you saved this code to a file and compiled it with tex, you probably already saw the error “TeX capacity exceeded”. The fact is that we forgot to ask to treat @ as an ordinary symbol, valid in macro names and variables. This can be done with the command

 \catcode `\@11 

(This is the same macro used in LaTeX under the alias \ makeatletter.)

In general, TeX can work with the fields of visibility of variables and macros, but it does not do so much the way it is done in ordinary programming languages. For example, try

 \def\addition{\newcount\s} 

declare a variable inside a macro to fail: "Forbidden control sequence found while scanning definition of \ a". There may be several roundabout maneuvers, but it is enough for us to agree to call the “local” (actually global) variables as <function name> @ <personal name> and be careful (!). After all of our macros, we will again make @ a special character using

 \catcode `\@12 

which prevents direct access to these variables from a later document.

Code testing \ testMod

Unitary divider and exponentiation

Next step: we will build a macro that calculates the maximum degree of one number, which still divides the other completely (if d is simple, then this is a unitary divisor ):

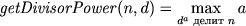
 \newcount\divisorpower %      , \newcount\getDivisorPower@m %   - n/d^a \def\getDivisorPower#1#2{ \getDivisorPower@m=#1 %   \divisorpower=0 % \testMod{\getDivisorPower@m}{#2} % ,    d \loop\ifdivisible % while-,   divisible \advance\divisorpower by1 %  a  1 \divide\getDivisorPower@m by#2 %   d \testMod{\getDivisorPower@m}{#2} %  ,    d \repeat %     } 

In C, this code would look like this (we write it intentionally clumsily):

 int divisible; int a; int m; void getDivisorPower(int n, int d){ m = n; a = 0; divisible = (m % d == 0); while(divisible){ a++; m /= d; divisible = (m % d == 0); } } 

Now a very easy macro:

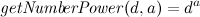
 \newcount\numberpower %        \newcount\getNumberPower@pow %   -      \def\getNumberPower#1#2{ \numberpower=1 %   \getNumberPower@pow=#2 \loop\ifnum\getNumberPower@pow>0 %   \multiply\numberpower by#1 \advance\getNumberPower@pow by-1 \repeat } 

Back to C:

 int numberpower; int pow; void getNumberPower(int d, int a){ numberpower = 1; pow = a; while(pow > 0){ numberpower *= d; pow--; } } 

It would be possible to implement a more efficient exponentiation algorithm , but this is enough for us.

It's time to make a check:

 \getDivisorPower{600}{2} \number\divisorpower \getDivisorPower{600}{3} \number\divisorpower \getDivisorPower{600}{5} \number\divisorpower \getDivisorPower{600}{7} \number\divisorpower 

should output "3 1 2 0", and

 \getNumberPower{5}{0} \number\numberpower \getNumberPower{6}{1} \number\numberpower \getNumberPower{7}{2} \number\numberpower 

will give "1 6 49".

Code testing \ getDivisorPower and \ getNumberPower

What's next?

Part 2, in which we will build a macro that considers the Euler function. For the most impatient - the working version of the macro . TeX easily handles calculations when n ~ 10 ⁹ .

Part 3, in which there will be even more sophisticated examples of mathematical calculations in TeX and, of course, benchmarks.