An experiment with holographic coding / decoding of color images

Once I was struck by one of the amazing properties of a hologram , which is that by breaking a holographic image of an object into fragments, an image of the whole object can be restored to each fragment, albeit with a somewhat degraded quality. After reading the topic “Experiment with holographic coding and decoding of information” by Comrade eresik, I certainly wanted to implement a similar digital hologram myself. Taking the algorithm as the basis, I launched Delphi and set to work. Finally, having fiddled a bit with the coefficients, I began to receive adequate black and white pictures similar to those that were received by eresik . When mashing a part of the hologram, surprisingly, the original image was restored! So how can this happen? I will try to tell you how you can clearly explain this property of a hologram, without going into physics and mathematics.



Consider the original object, which is an image with a single white dot and a hologram derived from it next to it:





')

As can be seen, the resulting hologram is a wave diverging from this point. And in the absence of the original image on these waves, you can restore the location of the source of these waves - our white point.



Result of the hologram-reconstructed image:





Yes ... and taking, for example, not a white, but a gray point (of less brightness), we will receive respectively the same waves of only gray (of less intensity). Those. on the hologram we can restore not only the position of the point, but also its brightness. Now we split off approximately half of the available hologram. Take a close look at the rest:







It becomes clear that even in this piece we can understand where the waves diverge from, and accordingly we can determine the position of the starting point.



Restored from a fragment of the hologram image:





Further, splitting the hologram into smaller parts in each of them, we have less and less information about the complete configuration of the waves and it will be more and more difficult for us to precisely localize the starting point.

Now we take the original image with two points and construct a hologram. In this case, on the hologram we will observe waves diverging from one and from another point. These waves will overlap, and the overall picture will be the sum of these waves.







In this picture, we can also easily determine the position of our points. Splitting off a certain part of the hologram again and again, we can determine from the remaining fragment where the points are located approximately.







Thus, each point of the hologram to a certain extent contains information about the whole object.



Adding more and more points to the original image, we will see more and more complex interference patterns. Visually, it is already very difficult to determine the appearance of the original image, for example, such a hologram:







However, it contains enough information to restore the original image of this quality:







In this case, you can see that the reconstructed image becomes noisy more than in the case of one or two points and you can hardly use anything other than a few contrast points as the original image. As eresik wrote, there are two reasons for strong noises. The first of these is that the brightness of the points is rounded to integers in the range 0..255. But as it turned out during the experiments, this factor does not play a decisive role. Mainly the noise level is determined by the resolution of the photographic plate. The above images used the resolution of the original 16x16 image and 256x256 pixels photographic plate, which is not bad, but the W wavelength was chosen too large for the sake of clarity = 2. Due to this, the waves were clearly visible, but the full potential of the resolution of the photographic plate was not used. By choosing a shorter wavelength W = 0.1, you can significantly reduce the level of noise.



Original, hologram and reconstructed image at W = 0.1:





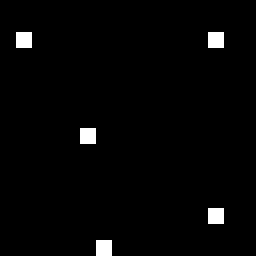
However, for the final resolution of the photographic plate, there is a limit of the minimum wavelength, passing which loud noise begins to appear.



Hologram and reconstructed image for W = 0.003:





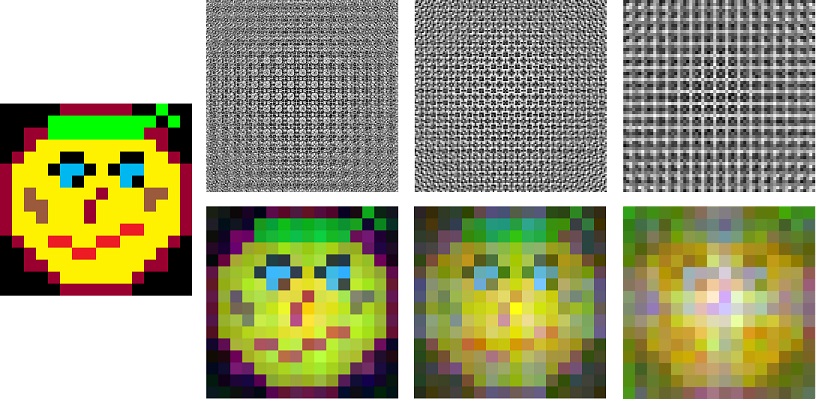
I slightly improved the algorithm of comrade eresik by adding color image processing. Like the production of a real hologram on a photographic plate, the interference of waves of three different lengths corresponding to red, green and blue light is exhibited. Also now the resolution of the hologram may be different from the resolution of the original image.

At the beginning of the topic you could see an example of the recovery of 16x16 color pictures from 192x192, 128x128, 64x64 photographic plates and WR = 0.03 wavelengths; WG = 0.029; WB = 0.028. Below is the case of restoring the original 32x32 image for a 192x192 photographic plate with the same parameters:







That is, it can be seen that, depending on the chosen resolution, we get when decoding an image of different quality.



And, at the end, you can try the program in action yourself, use various input data, change resolution, wavelengths. The program allows you to download bmp files as source images, make changes to them, mash up the noise of a hologram, and also calculate the degree of difference between the reconstructed image and the original one based on the brightness of the pixels. A difference of 100% means that the reconstructed image is inverted with respect to the original one.



Screen programs with unsuccessful attempt to recode Habr:





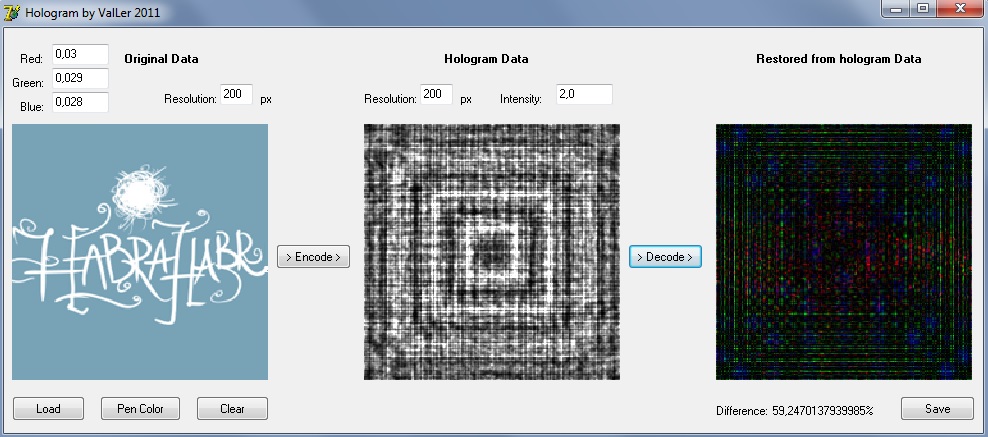
Program

Source