Arrays vs containers in matmodelling problems
Introduction
It so happened that my work is closely related to mathematical modeling of physical processes. Mathematical modeling is a very special area of programming. The calculation of even a relatively simple physical process can take several days or even weeks. Therefore, the performance of the program comes to the fore, even at the expense of the convenience of writing and reading code. However, until recently, the speed of my programs was of little concern to me: there were enough rough grids for which the calculations took about a day or so. But gradually the grids became more detailed, and the program runtime grew steadily. Then I began to look for bottlenecks in my program. First in the algorithms. Then it came to data structures. And here I was very interested in the question “what is better to use for storing vectors: arrays or containers?” In mathematical modeling, operations with large-dimension vectors and matrices, in particular, iterative methods for solving SLAEs, occupy one of the key positions. Theoretically, working with arrays should be faster, but working with containers is more convenient. The whole question is how to translate this "more" in the language of numbers? Is it worth the convenience of such costs? Search on the Internet did not give clear answers. There were either vague formulations from the category of “more or less”, “essentially-unimportant” or, at best, the simplest tests for repeated repetition of the same actions on elements of a vector. But tests are one thing, and combat reality is quite another. Moreover, having conducted some of these tests on my own, I was surprised to find that on different tests, different data structures have the advantage. Then, as a test, I decided to use a real physical problem.Task
As a test, I took the problem of convective flow known in thermal physics in an infinitely long square tube filled with liquid and heated from the side. Since the pipe has an infinite length (for definiteness, along the z coordinate) and the boundary conditions do not depend on z, the problem can be considered as two-dimensional. The left and right walls are maintained at constant, but different, temperatures. Upper and lower walls are insulated. On all walls, the conditions of impermeability and adhesion are specified, i.e. equality to zero of all components of speed. Convective heat transfer in a fluid is described by the system of equations of Navier-Stokes and continuity in the coordinates temperature-vortex-current function:
The problem was solved by the finite element method on a triangular grid with linear basis functions. The size of the ax is 100x100 knots. As a solver of SLAE, LOS with LU preconditioning was used.
Source codes
Source codes of programs can be found here .Test results
So. Actually for what it was all started. It was written three software implementation of the solution of the above tasks. C ++ was used as a programming language. In the first program, dynamic arrays were used to store matrices and vectors, in the second, std :: vector containers, and in the third, QVector containers. The program work times (in ticks) are presented in the table:| Release | |||||||
| one | 2 | 3 | four | five | The average | Loss of time | |
| Arrays | 21820000 | 21760000 | 21730000 | 21660000 | 21850000 | 21764000 | 0% |
| std :: vector | 26680000 | 26660000 | 26900000 | 26870000 | 26790000 | 26780000 | 23% |
| QVector | 43760000 | 43770000 | 43820000 | 43840000 | 43770000 | 43792000 | 101% |
| Debug | |||||||
| one | 2 | 3 | four | five | The average | Loss of time | |
| Arrays | 50290000 | 50630000 | 50760000 | - | - | 50560000 | 0% |
| std :: vector | 118830000 | 119560000 | 118240000 | - | - | 118877000 | 135% |
| QVector | 306800000 | 297400000 | 294400000 | - | - | 299530000 | 492% |
findings
So, the main conclusion from the test results can be drawn as follows: the use of containers is unacceptable when solving the problems of mathematical modeling. No convenience in writing code, no security code can justify a drop in performance of 23%. Frankly, I did not expect such a noticeable fall. The results of QVector's testing became an even more unpleasant surprise for me, because I used it in my program. This serious lag seems to be due to the use of the concept of SharedMemory. Saving on copying, we lose on access to the elements of the container, because when you change each! element is an additional check for the need to perform deferred copying.Bonus: Mathematical Simulation Results
Temperature: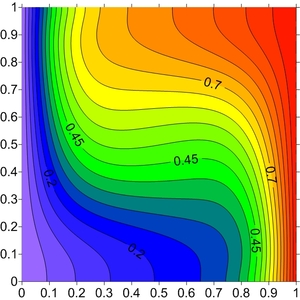 | Current function: |
Vortex: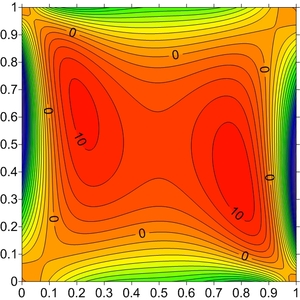 | Vx: |
Vy: |
')
Source: https://habr.com/ru/post/122036/
All Articles