Generating random numbers on microcontrollers

A lot is written about random number generators, but almost always, when it comes to implementation, it is implied (or explicitly stated) that we are talking about x86 / x64 and other “adult” architectures. At the same time, the forums dedicated to the development of devices on microcontrollers are full of questions “how do I generate a random number on% controllername%?”. Moreover, the range of answers extends from “see Google / Wikipedia” to “use the standard function”. Not always, this “standard function” exists and suits the developer in all respects, more often the other way around: either the numbers are far from random, the speed is too low, or the resulting code does not fit in the free memory at all.
Let's try to figure out what random number generation algorithms are, how to choose the right one, and most importantly, what are the features of the implementation of these algorithms on controllers.

Evaluation of "randomness"

Applications for RNG can be found very different, from toys to serious cryptography. Accordingly, the requirements for the generator also vary greatly. To assess the quality (level of "randomness") of the generator, there are special tests. Here are the most basic ones:

• Frequency test. It consists in counting the number of zeros and ones in the sequence of bits. Units and zeros should be approximately equal.
• A test for a sequence of identical bits. Rows of the same bits are searched for, of the type 000 ... 0 or 111 ... 1. The distribution of frequencies with which the series are encountered, depending on their length, must correspond to such a distribution for a truly random signal.
• Spectral test. A discrete Fourier transform is applied to the source sequence. The resulting spectrum should not have significant peaks, which would indicate the presence of periodic sequence properties.
• Autocorrelation test. The correlation value between copies of a sequence that are shifted relative to each other is calculated. The test allows you to find duplicate areas in a sequence.

There are special kits that include dozens of similar tests:
NIST - used in the AES competition for evaluating encryption algorithms.
DIEHARD is one of the most stringent existing kits.
')

GPSL Algorithms

Any sequence generated by a strictly defined algorithm cannot be considered truly random, therefore, when speaking of algorithmic generators, the term pseudo-random sequence is used. Any pseudo-random number generator (PRNG) sooner or later loops in, another thing is that this “late” may occur in a few milliseconds, or maybe in a few years. The cycle length depends on the size of the internal state of the generator N (in fact, it is the amount of memory needed by the generator), and ranges from 2 ^{(N / 2)} to 2 ^N bits.
The PRNG algorithms are invented a great many, but not all of them are convenient for implementation on microcontrollers. We are very limited in speed and available memory, many controllers do not support real arithmetic and even multiplication commands. Bearing in mind these limitations, consider some well-known algorithms.

Linear congruential method

The next member of the sequence is calculated by the formula
X _{i + 1} = (aX _i + c) mod m
The number m determines the maximum period of the sequence, the integers a and c are the "magic" coefficients. The number m is reasonable to choose equal to the power of two, in which case the operation of reduction along the module reduces to discarding the higher bits. In order to get the maximum period, you must comply with the following conditions:
- c and m must be mutually simple,
- a-1 must be a multiple of p for all prime dividers p of the number m ,
- if m is a multiple of 4 (and in our case it will be a multiple), then a-1 must be a multiple of 4.
There is one more subtlety: as a result, only the high-order bits of the state variable X should be taken, since for the lower bits the statistical parameters of randomness are much worse. A linear congruential algorithm is usually implemented as a standard rand () in many libraries.

Pros:

• the maximum possible period for a given size of a state variable;
• fast enough;
• often already implemented in the compiler library.

Minuses:

• multiplication operation is required;
• not all bits are equally random.

Summary: fast and simple algorithm for not very demanding applications.

Fibonacci latency method

This algorithm uses the ratio
X _i = X _ia - X _ib ,
where the state variable X is an unsigned integer. The magnitude of the delays a and b are not taken any, but strictly defined, to achieve the highest quality pairs (17.5), (55,24) or (97,33) are recommended. The greater the delay, the longer the period and the better the spectral properties of the sequence. On the other hand, for the operation of the generator, it is required to store max {a, b} of the previous numbers, which is not always acceptable. Also, to start the generator, you need max {a, b} numbers, which are usually obtained using a simpler PRNG.

Pros:

• does not require multiplication operations;
• all bits of a random number are equivalent in statistical properties.

Minuses:

• requires a large amount of memory;
• requires a large array of numbers to run.

Summary: very high-quality, but resource-intensive algorithm.

Shift register with linear feedback

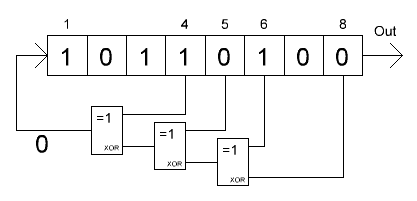
The state variable is stored in the length register N. Generation of the following state involves two steps:

1. The value of the C = X _i1 xor X _i2 xor ... X _ik bit is _calculated , where i1, i2 ... ik are the numbers of the register bits called taps .
2. The register is shifted 1 bit to the right, the leftmost bit is C.

The generator output is the rightmost (or leftmost, or any other) bit of the register, that is, the pseudo-random sequence is generated one by one bit per iteration. With correctly selected numbers of taps, the period of the generator will be 2 ^N - 1. "Minus one", since there is a prohibited zero register state. The numbers of taps for N from 3 to 168 can be found in this document .
In addition to the configuration described above, which, by the way, is called the Fibonacci configuration (not to be confused with the PRNG method of the same name!), There is a so-called Galois configuration.

Instead of using the sum of the bits of the tap sequence to generate a new leftmost bit, XOR each bit of the tap sequence with the rightmost bit, then the entire register is cyclically shifted to the right. This scheme is more difficult to understand, but easier to implement, since all XOR operations can be performed simultaneously. For the length of the period and the quality of pseudo-random numbers, the Fibonacci and Galois schemes are equivalent.

Pros:

• very simple implementation, even arithmetic is not required, only bit operations and shifts;
• very fast algorithm (especially Galois scheme);
• good statistical properties.

Minuses:

• you need to check the initial value for zero inequality.

Summary: very fast and fairly high-quality algorithm.

Crypt-resistant algorithms

For use in cryptography to GPSCH, there is one more essential requirement: irreversibility . All the above algorithms do not have this property: knowing several output PRNG values, you can, having solved a simple system of equations, find the parameters of the algorithm (the very “magic” constants a, b, s , etc.). And knowing the parameters, you can reproduce the entire pseudo-random sequence.
As a cryptographically robust PRNG algorithm, you can use any sufficiently strong block cipher. By choosing a secret key, you can get blocks of pseudo-random numbers by applying the algorithm to consecutive natural numbers. For an N-bit block cipher, the period will be no more than 2 ^N. The security of such a scheme depends entirely on the secrecy of the key.
All modern cryptographic algorithms are tested for use as a PRNG, that is, using a certified algorithm, you do not need to specifically take care of the statistical and spectral properties of the output stream. You only have to worry about the computational “gluttony” of cryptoalgorithms. If you need to perform a large number of encryption operations, it makes sense to choose a controller with hardware cryptographic blocks. Often in such controllers there is also a quite good crypto-resistant hardware PRNG.

Sources of entropy

As already mentioned, using only deterministic algorithms, it is impossible to generate a truly random number. Therefore, a PRNG + external entropy source is usually used. The entropy source is used to set the initial value for the PRNG, and the task of the latter is to ensure the spectral and statistical purity of the sequence. So what can be used as a source of entropy? Yes, almost anything.

User activity

If the device interacts with the user in any way, it will be a pretty good solution to use the user as the source of entropy. For example, the time it takes to press a button, measured to the nearest microsecond (or rather, its low-order bits), is completely unpredictable. However, often the device must work autonomously, which means we lose this wonderful information channel.

Analog-to-digital converter

Many controllers have built-in ADCs. And in many controllers, they are of very mediocre quality, made simply “for it to be”. The low-order bits of the ADC result almost always contain significant noise, even if a constant voltage is measured. This can be used: connect the ADC input to the supply voltage through a divider, take a few dozen measurements, take the low-order bits — this is a great random number. If the ADC contains a built-in preamp, turn it on, it also makes noise.

Asynchronous generators

You can use the difference of the periods of two unsynchronized clocks. Most controllers contain, for example, a watchdog timer. To increase reliability, it is clocked from a separate generator that is not related to the main clock signal. It is enough to count the number of clocks of the main clock signal for one period of the watchdog timer. If you select the periods so that the counter overflows many times during the measurement, you can get a fairly random number. The disadvantage of this method is that it takes a lot of time, up to several seconds.

Real time clock

If the circuit has a real-time clock , you can use their current readings to initialize the PRNG. For example, converting the current date / time to the Unix time format, we will get 32 ​​bits at once, which will never happen again, unless we take readings more often than once per second. Using real-time gives a unique value, but does not give any unpredictability, so it is better to combine this method with others.

RC circuit

If the controller does not have any peripheral devices other than I / O ports, you can proceed as follows: one of the legs is connected to ground via a capacitor, and to the supply voltage through a resistor. If the controller inputs have internal pull-up resistors, no external resistor is needed.

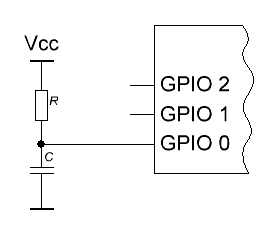
We output the signal "0" to this port - the capacitor discharges. We switch the port to the input mode - the capacitor starts charging. When the voltage on it reaches the threshold, the input switches from the state "0" to "1". Charging time is highly dependent on many factors: power supply voltage, RC circuit parameters drift, threshold instability, temperature, leakage, interference. Measuring it with sufficient accuracy and taking the lower bits, you can get a good chance.

Noise generator

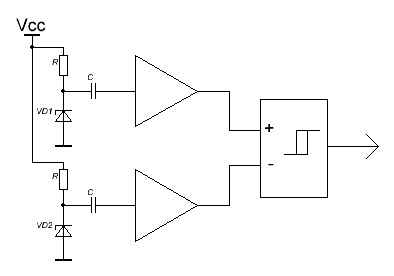
For many serious applications (primarily cryptography is meant), a more reliable source of entropy is required than those listed above. In such cases, digitizing the signal from a noise generator based on thermal , shot , or even quantum effects is used. A noisy element is usually a special diode or zener diode, the signal from which is amplified and fed to a comparator that forms a binary bit stream.

To ensure that the threshold of the comparator does not affect the statistical properties of the received signal, two noise generators are used, which operate on one comparator:

Conclusion

Finally, I will tell one story from life. It began with the next question asked on the forum “how do I generate a random number on the controller?”. The author of the question explained what a device that emulates the throwing of a dice is doing as a course project. After several unsuccessful attempts to understand the algorithms, the topstarter shared his decision: he simply threw a real cube 1000 times and scored all the free memory of the controller with the resulting numbers. The generator brilliantly passed all tests for “randomness”, considering that during the demonstration it spent less than a third of its “stock”.
Therefore, such a decision also has the right to life, especially if very strict requirements are imposed on the randomness of numbers, but they are not required too often. Given the rapidly falling prices of memory, it may be reasonable to provide a device with a flash drive with a “margin of chaos” that will last for the entire lifetime of the device.
Thank you for attention!

UPD1: As was rightly noted in the comments, if an attack on the RNG is intended, and the attacker will have hardware access to the device, external sources of entropy need to be used with great caution, since it is not very difficult to replace the signal from an external source. Internal sources should be used, in addition to external sources.
It is also a good idea to accumulate entropy all the free time, and use it when you need to generate another random number. Usually in such cases, so-called. Entropy pool is an array, on which one of the PRNG functions is periodically performed, and where data from entropy sources are constantly mixed.

UPD2: In many cases, the contents of the Entropy pool (sorry, I don’t know the normal Russian translation) are useful to save in the EEPROM so that after switching off and on the device it does not accumulate again. First of all, it is related to the entropy obtaining by the method of asynchronous generators: under sufficiently stable conditions, after each switch-on, the same sequence can be generated.
If an attack is expected, take action against spoofing the EEPROM contents. If the controller allows, block reading / erasing / writing using lock bits, when turned on, check the integrity of the EEPROM, at least with the help of the simplest checksums.