Who breeds fish? Or solving Einstein's riddle in regular language
Many were faced with a puzzle about five colorful houses, in each of which a person lives with their favorite animals, drinks and cigarettes. This riddle is attributed to Einstein, although there is no direct evidence of this. The full text of this puzzle is on Wikipedia .
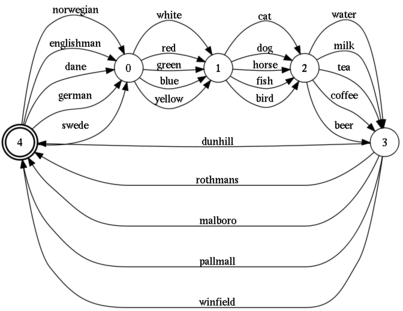
It can be solved on paper or in the mind, consistently eliminating inappropriate options. However, it can also be solved more technically. One way is to write a program on the prologue. But here I want to solve it using simpler mechanisms - regular expressions. Namely, translate the riddle conditions into the regexp language and reduce the task to finding the appropriate string in the entire admissible set of strings. By the way, this rowset is shown in the figure.
')
The idea itself is not mine, I heard it in one video lecture. However, there it was solved too sophisticated. I tried to solve it more simply and straightforwardly.
For convenience, here is the riddle text:
Question: who breeds fish?
To solve the problem you need to find a sequence of houses, flowers, nationalities, drinks and cigarettes, so that they satisfy the rules above.
And so what and where will we look. First you need to somehow formalize the rules. We have five houses, flowers, nationalities, drinks, animals and cigarettes. Arbitrary version of the house with the "tenants" may look like this:
But this is not enough, since we have rules that take into account the relative position of houses and objects in them (for example, the rules: 1, 3, 5 ...). We take this into account by placing five houses in a row in a row:
The line above is one of the options for the location of objects. In this case, incorrect. If we make up all the possible options and put it in one text, we get the following:
Where n is nation, c is color, a is animal, d is drink, s is cigarettes. And each of these letters can take one of its five meanings.
Wonderful. What remains to be done is to translate the rules into a regular expression language:
And if the line fits all the rules, then we have found a solution! It only remains to see the nationality in the house with the fish. This is the main idea of the search: to build a text and walk on it with regular expressions.
But there is bad news. The text that will be searched can be VERY large. More specifically, it will be (5!) ^ 5 lines (~ 24 billion). Its not really to check, it will be difficult to even generate it. But there is good news. We can not generate all this text, but use the regular expression intersection operation. That is, we find all common strings of a regular expression * (all possible strings), with those strings that give regular expressions for the rules of the problem . That line (and maybe the line) that remains after the intersection will be the solution to the problem.
Unfortunately, I don’t know engines that can intersect regular expressions. Therefore, it is necessary to use directly the finite automata underlying any regexp.
I will build state machines using the openfst library. It provides everything I need to build automata, plus a convenient way to work from a shell. To make programming even more “abnormal”, I will not program at all :). With the exception of simple bash scripts, there will be no code.
Create a text file with a list of all objects. This will be our alphabet.
We construct basic automata, each of which allows only one word from the alphabet.
fstcompile is the openfst package command that compiles the textual representation of the machine into a binary. This is necessary in order to then apply various operations to this machine.
And so, we have a list of file-machines. They are very trivial. For example, the beer machine will look like this:
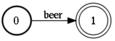
It is equivalent to the regular expression "beer". So far, it's pretty simple. In addition, we will need two more basic automata - an empty set, and any string, i.e. asterisk *. Build.
Empty line, machine 'empty':
Asterisk, automat 'star':
The latter is done by simply combining the base automata and closing. In regular expressions, this is just (englishman | dane | ... | cat | dog | ...) *. This machine will be:
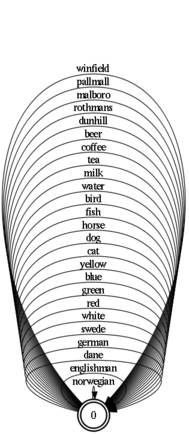
It will be more convenient to describe the rules if you create more complex automata such as nationality, color, etc. Again, I use a simple script:
Rules 5, 9 and 12 are compound. I define each part separately, and then I do the union. The concat.sh script only does the concatenation of the automata passed in the arguments:
So, at the output we get automata r1, r2 ..., r15. Everything is ready for the final step.
Where intersect.sh is the intersection of automata in arguments.
On this one could finish - look at the machine and find out who the fish is. But from the very beginning I did not take into account one thing - in my rules each of the words can be repeated. For example, two people can drink one beer and start one animal. This is incorrect by the conditions of the problem. It is extremely inconvenient to create such a filter using regular languages, since we have no way to "remember" that such a word already existed. But it is somehow necessary to limit. According to this, we subject the final result to the following script.
This script generates a special automat for each word from the alphabet, and applies it to the result. Thus, the path swept away with repeated words. As a result, the final result (and in fact, the 'out' automaton) looks like this:

This is a partial image of the machine (all is not fit). Every five words define a house. As can be seen from the figure, the German breeds fish.
Here is such an unusual way to solve the problem. But among other things, it shows that regular languages are a pretty powerful thing. Moreover, according to Ulman, any mathematical problem can be represented as finding a string in a certain language . What was shown.
ps and yes, the mouse really knows a lot about perversions :)

It can be solved on paper or in the mind, consistently eliminating inappropriate options. However, it can also be solved more technically. One way is to write a program on the prologue. But here I want to solve it using simpler mechanisms - regular expressions. Namely, translate the riddle conditions into the regexp language and reduce the task to finding the appropriate string in the entire admissible set of strings. By the way, this rowset is shown in the figure.
')
Idea
The idea itself is not mine, I heard it in one video lecture. However, there it was solved too sophisticated. I tried to solve it more simply and straightforwardly.
For convenience, here is the riddle text:
- Norwegian lives in the first house.
- The Englishman lives in a red house.
- The green house is to the left of the white one, next to it.
- Dane drinking tea
- One who smokes Marlboro lives next to one who grows cats.
- The one who lives in the yellow house smokes Dunhill.
- German smokes Rothmans.
- The one who lives in the center drinks milk.
- The neighbor of the Marlboro smoker is drinking water.
- One who smokes Pall Mall grows birds.
- Swede breeds dogs.
- Norwegian lives near the blue house.
- The horse grower lives in the blue house.
- The one who smokes Winfield drinks beer.
- In the green house they drink coffee.
Question: who breeds fish?
To solve the problem you need to find a sequence of houses, flowers, nationalities, drinks and cigarettes, so that they satisfy the rules above.
And so what and where will we look. First you need to somehow formalize the rules. We have five houses, flowers, nationalities, drinks, animals and cigarettes. Arbitrary version of the house with the "tenants" may look like this:
german white cat beer malboro But this is not enough, since we have rules that take into account the relative position of houses and objects in them (for example, the rules: 1, 3, 5 ...). We take this into account by placing five houses in a row in a row:
german white cat beer malboro englishman red dog water pallmall norwegian green fish milk winfield dane blue bird tea dunhill swede horse yellow coffee rothmans The line above is one of the options for the location of objects. In this case, incorrect. If we make up all the possible options and put it in one text, we get the following:
ncadsncadsncadsncadsn cads ncadsncadsncadsncadsn cads ncadsncadsncadsncadsn cads ... Where n is nation, c is color, a is animal, d is drink, s is cigarettes. And each of these letters can take one of its five meanings.
Wonderful. What remains to be done is to translate the rules into a regular expression language:
- ^ norwegian \ w +
- \ w + englishman red \ w +
- \ w + dane \ w \ w tea \ w +
- ...
And if the line fits all the rules, then we have found a solution! It only remains to see the nationality in the house with the fish. This is the main idea of the search: to build a text and walk on it with regular expressions.
But there is bad news. The text that will be searched can be VERY large. More specifically, it will be (5!) ^ 5 lines (~ 24 billion). Its not really to check, it will be difficult to even generate it. But there is good news. We can not generate all this text, but use the regular expression intersection operation. That is, we find all common strings of a regular expression * (all possible strings), with those strings that give regular expressions for the rules of the problem . That line (and maybe the line) that remains after the intersection will be the solution to the problem.
Unfortunately, I don’t know engines that can intersect regular expressions. Therefore, it is necessary to use directly the finite automata underlying any regexp.
Implementation
I will build state machines using the openfst library. It provides everything I need to build automata, plus a convenient way to work from a shell. To make programming even more “abnormal”, I will not program at all :). With the exception of simple bash scripts, there will be no code.
Step 1 - Build basic automata
Create a text file with a list of all objects. This will be our alphabet.
norwegian englishman dane german swede white red ... We construct basic automata, each of which allows only one word from the alphabet.
j=1 for i in `cat alph`; do echo -e "0 1 $j\n1" | fstcompile --acceptor > $i ((j=$j+1)) done fstcompile is the openfst package command that compiles the textual representation of the machine into a binary. This is necessary in order to then apply various operations to this machine.
And so, we have a list of file-machines. They are very trivial. For example, the beer machine will look like this:

It is equivalent to the regular expression "beer". So far, it's pretty simple. In addition, we will need two more basic automata - an empty set, and any string, i.e. asterisk *. Build.
Step 2 - Building an empty machine and an asterisk
Empty line, machine 'empty':
echo '0' | fstcompile --acceptor > empty Asterisk, automat 'star':
cp empty star for i in `cat alph`; do fstunion star $i star done fstclosure star star The latter is done by simply combining the base automata and closing. In regular expressions, this is just (englishman | dane | ... | cat | dog | ...) *. This machine will be:

Step 3 - Building Houses
It will be more convenient to describe the rules if you create more complex automata such as nationality, color, etc. Again, I use a simple script:
c="./concat.sh" $c norwegian star > r1 $c star englishman red star > r2 $c star animal drink cigarette nation star > r3 $c star dane color animal tea star > r4 $c star malboro nation color cat star > r5_0 $c star cat drink cigarette nation color animal drink malboro star > r5_1 $c star yellow animal drink dunhill star > r6 $c star german color animal drink rothmans > r7 $c house house nation color animal milk cigarette house house > r8 $c star malboro nation color animal water star > r9_0 $c star water cigarette nation color animal drink malboro star > r9_1 $c star bird drink pallmall star > r10 $c star swede color dog star > r11 $c star norwegian color animal drink cigarette nation blue star > r12_0 $c star blue animal drink cigarette norwegian star > r12_1 $c star blue horse star > r13 $c star beer winfield star > r14 $c star green animal coffee star > r15 fstunion r5_0 r5_1 > r5 fstunion r9_0 r9_1 > r9 fstunion r12_0 r12_1 > r12 Rules 5, 9 and 12 are compound. I define each part separately, and then I do the union. The concat.sh script only does the concatenation of the automata passed in the arguments:
cp empty _c for i in $*; do fstconcat _c $i _c done; cat _c; rm _c; So, at the output we get automata r1, r2 ..., r15. Everything is ready for the final step.
Step last - Crossing
./intersect.sh r1 r2 r3 r4 r5 r6 r7 r8 r9 r10 r11 r12 r13 r14 r15 > result Where intersect.sh is the intersection of automata in arguments.
cp cl _c for i in $*; do fstintersect _c $i _c done; cat _c; rm _c; On this one could finish - look at the machine and find out who the fish is. But from the very beginning I did not take into account one thing - in my rules each of the words can be repeated. For example, two people can drink one beer and start one animal. This is incorrect by the conditions of the problem. It is extremely inconvenient to create such a filter using regular languages, since we have no way to "remember" that such a word already existed. But it is somehow necessary to limit. According to this, we subject the final result to the following script.
i="./intersect.sh" d="fstdifference" for i in `cat alph`; do fstdifference cl $i > differ fstconcat differ $i | fstconcat - differ | fstrmepsilon - | fstdeterminize - | fstminimize - > ${i}_cont done cp result out for i in `ls *_cont`; do echo $i fstintersect $i out | fstrmepsilon - | fstdeterminize - | fstminimize - out done rm differ rm *_cont This script generates a special automat for each word from the alphabet, and applies it to the result. Thus, the path swept away with repeated words. As a result, the final result (and in fact, the 'out' automaton) looks like this:

This is a partial image of the machine (all is not fit). Every five words define a house. As can be seen from the figure, the German breeds fish.
Conclusion
Here is such an unusual way to solve the problem. But among other things, it shows that regular languages are a pretty powerful thing. Moreover, according to Ulman, any mathematical problem can be represented as finding a string in a certain language . What was shown.
ps and yes, the mouse really knows a lot about perversions :)
Source: https://habr.com/ru/post/121061/
All Articles