Lamport hash chain - insurance against theft of the customer password database
A very interesting post recently published on Habré, and especially the comments to it, pushed me to the description of, perhaps, the only symmetric scheme that really provides insurance against theft of the password database from the server - Lamport's scheme (“Lamport hash chain”). The algorithm is in fact extremely simple and proposed by the author (L.Lamport) in 1981. Moreover, the scheme in most textbooks is already referred to as “outdated”, since The purpose of its development was, first of all, protection against password interception at the transfer stage, and the later “challenge-handshake” family of schemes (CHAP, CRAM) appeared to solve this problem much more effectively. But the second interesting property of the Lamport scheme is already slowly forgotten - it does not require the confidentiality of user authentication data stored on the server side (a property that is usually inherent only in asymmetric schemes with client certificates). Let us see how this property can be achieved with the help of a crypto-resistant hash function alone.
We formulate the problem in terms of cryptography (we construct a threat model).
A) The server stores data that allows the client to be authenticated.
B) The disclosure / theft of this data should not allow an attacker to impersonate a client in front of the server.
C) Disclosure / audition (including multiple) of the data transmitted between the client and the server at the authentication stage (“listening to the protocol”) should also not allow an attacker to successfully impersonate that client afterwards.
D) The protection task from an active attacker-proxy (“man-in-the-middle”) is not assigned.
E) In the event of a server hacking, we believe that the attacker could only violate the confidentiality, but not the integrity of the authentication data base (the violation of integrity can be monitored with additional control mechanisms).
Obviously, in the event of theft of the authentication data base, the attacker has exactly the same information as the server. And, therefore, the process of verifying the authenticity of the client should be carried out by the server so that it could verify the client’s validity, and could not pass it on his own (speaking on behalf of the client). Checking the comparison of any data (password, cipher, etc.) such properties can not be achieved. The check should be carried out on the client's ability to do something that no one else can do (including the server). In symmetric cryptography, the only such transformation is the calculation of a crypto-resistant hash.
')
Well, now the actual essence of the scheme.
The process of installing authentication data
Authentication process
Each time you need to verify the authenticity of the user:
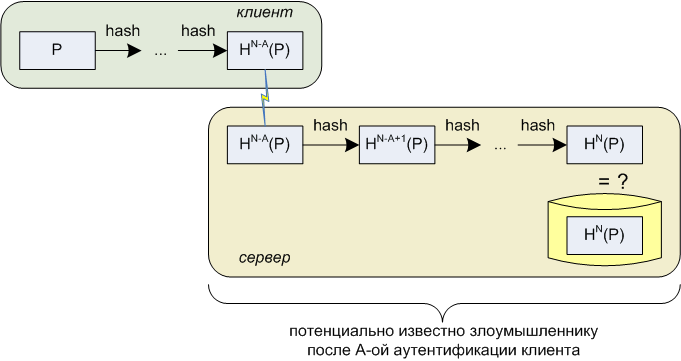
Requirements B) and C) in relation to the Lamport scheme turn into essentially one thing: if the counter value is A, the attacker has any set (including possibly complete) of values from the list H N-A + 1 (P), H N-A + 2 (P), ..., H N (P) should not be able to successfully pass authentication for either the value of the counter A, or for any other value greater than A. Is this true? First, it can be noted that the entire list listed above is equivalent in value to the attacker to one — the very first value of H N – A + 1 (P) (since the rest are easily calculated from it). Does knowing H N-A + 1 (P) with an unknown P make it possible to calculate H NA (P)? No doubt not, since this task is the problem of finding the prototype of a crypto-resistant hash function by its known value. With a sufficiently large power of the input value space, this task still has no solution in a reasonable time, despite the recent achievements of cryptoanalysis of hash functions.
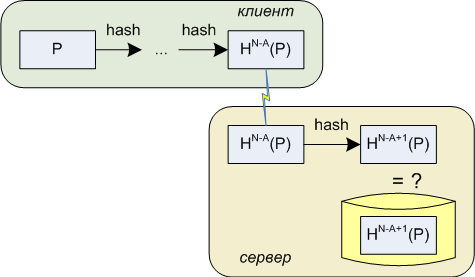
A fairly obvious improvement in the scheme, which does not affect its durability in any way, is storing on the server side not H N (P) values with constant checking from A operations, but H N – A + 1 (P) values with checking from just one hash calculation : H (H NA (P))? H N-A + 1 (P). This option requires updating the authentication data field every time the client logs in, but updating A still has to be done, so the negative impact is much less, and the positive is a sharp decrease in the CPU load on the server, since the need for an A-fold hash calculation disappears.
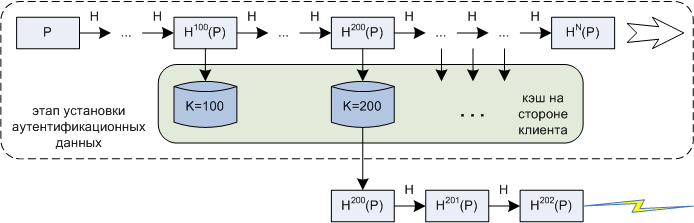
In those years, when the scheme was proposed, the calculation of thousands of hash functions was considered to be a very computationally complex process, therefore, an improvement on the client side was also proposed: caching intermediate values with a certain step in the process of initial calculation of H N (P). This made it possible to speed up the computation of the client response, but, like any caching, it required additional long-term storage resources (and they also had to be subject to confidentiality requirements similar to the P password itself). Nowadays, calculating 100,000 iterations of the hash function even on a weak PC takes about a second. Therefore, such caching can be recommended only for the weakest hardware platforms.
The main problem of the Lamport scheme is, of course, an active malefactor ("man-in-the-middle"). Obviously, in the absence of server authentication to the client before sending a response, an attacker, sending allegedly more than the current value of the counter A 'on behalf of the server, can get the value H N-A' (P) from the client and then calculate any value from the range H N-A ' (P) ... H NA (P). The storage of the current value of the counter A for server control offered by some sources on the client does not actually solve the problem, because if we accept the threat of an intermediary attacker, then he is still able to intercept and suppress the correct client packet H NA (P ), authenticate with his help already from his station.
For the same reason, it does not make sense in this threat model to increase Counter A with any authentication request, regardless of whether it was successful or not, as suggested in some implementations. This scheme creates the threat of exhaustion (DoS) of the counter by the attacker and still does not protect against the attacker intermediary. The author himself in the original work does not recommend changing the counter in an unsuccessful attempt.
SSL (with one-way server authentication in front of the client) can provide optimal protection against both threats today. Once again, the “two-way” SSL with client authentication in front of the server with its certificates, of course, solves the whole problem of password theft in general. But it is an order of magnitude heavier both for deployment and for support with a large number of customers. Here, all the problems can be solved by the “one-way” SSL with a properly signed server certificate, which allows the client to report the next values of H K (P) only to the legitimate server.
There are certain problems with the Lamport scheme when restoring a server system from a backup if the recovery scheme implies an RPO greater than 0. In this case, the client’s successful authentications, overheard by the attacker, could potentially go through the “lost” period of time, and the counter value A recovered from the backup to dictate to the server to submit the previously observed A. value in the request again. Lamport himself suggests, in the case of restoration from the backup, to increase A by the average expected number of events a authentication for the time the system is offline, with some margin.
Reinitialization
And the last problem of the scheme: what to do when the counter of authenticated authentication A approaches the value of N? This situation is called reinitialization. In the original version of Lamport, the reinitialization implies a complete regeneration of the authentication information, that is, the replacement of P on the client side and H N (P) on the server side. If P is generated from a user password, respectively, either the hash amount needs to be entered, in addition to the server name, also the rekey initialization sequence number rekey_id: P = H (password || servername || rekey_id), store it on the server and inform the client in each request . Or, with each reinitialization, change the user's password and in any way ensure the complete non-repeatability of passwords, which seems to me a more difficult technical task. By the way, to protect against an attack on a password using a known P, it is not bad to re-initialize it at least 1 step before the Nth authentication, so that the client does not have to send the value P via an open channel.
Over the last 7-8 years, several more modern works on self-initializing hash chains have been published (they can be found in the search for the terms “re-initializable hash chains”, “infinite hash chains” or “self-updating hash chains”). However, I want to say that the mathematics there is very, very nontrivial, which is why the beauty of the idea of Lampert comes down almost to nothing.
Finally, if counter A increases (as in the original version) only after successful authentication, and clients have sufficient computing power, then re-initialization can be avoided altogether by simply setting N equal to, say, 100,000 (for 30 years with 10 authentications per day) that seems to me the most sensible solution.
In general, the Lamport scheme is a viable and much simpler alternative to asymmetric client authentication, which is somewhat unreasonably forgotten today.
Formalized task description
We formulate the problem in terms of cryptography (we construct a threat model).
A) The server stores data that allows the client to be authenticated.
B) The disclosure / theft of this data should not allow an attacker to impersonate a client in front of the server.
C) Disclosure / audition (including multiple) of the data transmitted between the client and the server at the authentication stage (“listening to the protocol”) should also not allow an attacker to successfully impersonate that client afterwards.
D) The protection task from an active attacker-proxy (“man-in-the-middle”) is not assigned.
E) In the event of a server hacking, we believe that the attacker could only violate the confidentiality, but not the integrity of the authentication data base (the violation of integrity can be monitored with additional control mechanisms).
The main idea of the method
Obviously, in the event of theft of the authentication data base, the attacker has exactly the same information as the server. And, therefore, the process of verifying the authenticity of the client should be carried out by the server so that it could verify the client’s validity, and could not pass it on his own (speaking on behalf of the client). Checking the comparison of any data (password, cipher, etc.) such properties can not be achieved. The check should be carried out on the client's ability to do something that no one else can do (including the server). In symmetric cryptography, the only such transformation is the calculation of a crypto-resistant hash.
')
Well, now the actual essence of the scheme.
The process of installing authentication data
- The client and server agree on the number N (from the range, say from 1.000 to 100.000) - this value is non-secret and can be just hard-coded.
- The client chooses a random number P of a large dimension (128 bits or more):
- or calculates it using the hash function from the user password and server name P = H (password || servername);
- either generates it from trusted sources of random / pseudo-random numbers and keeps it on its side (the disadvantage is the “linking” to the client station or the need to use tokens). - The client performs N times recursively cryptographically hashing H over the number P and transmits the result H (H (H (... H (P))) = H N (P) to any server protected from modification to the server ( Attention! The entry H K (P) throughout the paper will be used to denote the superposition (K-fold call repetition) of the hash function, rather than raising its result to the power of K ).
- The server initializes counter A of the sequence number of the upcoming client authentication number 1.
Authentication process
Each time you need to verify the authenticity of the user:
- The server sends the number A.
- The client performs (NA) times hashing over the P number and sends the resulting result H NA (P) to the server.
- The server performs another hashing over the number H NA (P) A again and compares the result H A (H NA (P)) with H H N (P) stored in it.
- If the result matches, the client is considered to have successfully confirmed its authenticity, and the server increments the count of successful authentications by 1: A = A + 1, thereby “shifting” along the chain one position to the left .

Proof of required properties
Requirements B) and C) in relation to the Lamport scheme turn into essentially one thing: if the counter value is A, the attacker has any set (including possibly complete) of values from the list H N-A + 1 (P), H N-A + 2 (P), ..., H N (P) should not be able to successfully pass authentication for either the value of the counter A, or for any other value greater than A. Is this true? First, it can be noted that the entire list listed above is equivalent in value to the attacker to one — the very first value of H N – A + 1 (P) (since the rest are easily calculated from it). Does knowing H N-A + 1 (P) with an unknown P make it possible to calculate H NA (P)? No doubt not, since this task is the problem of finding the prototype of a crypto-resistant hash function by its known value. With a sufficiently large power of the input value space, this task still has no solution in a reasonable time, despite the recent achievements of cryptoanalysis of hash functions.
Effective implementation
A fairly obvious improvement in the scheme, which does not affect its durability in any way, is storing on the server side not H N (P) values with constant checking from A operations, but H N – A + 1 (P) values with checking from just one hash calculation : H (H NA (P))? H N-A + 1 (P). This option requires updating the authentication data field every time the client logs in, but updating A still has to be done, so the negative impact is much less, and the positive is a sharp decrease in the CPU load on the server, since the need for an A-fold hash calculation disappears.

In those years, when the scheme was proposed, the calculation of thousands of hash functions was considered to be a very computationally complex process, therefore, an improvement on the client side was also proposed: caching intermediate values with a certain step in the process of initial calculation of H N (P). This made it possible to speed up the computation of the client response, but, like any caching, it required additional long-term storage resources (and they also had to be subject to confidentiality requirements similar to the P password itself). Nowadays, calculating 100,000 iterations of the hash function even on a weak PC takes about a second. Therefore, such caching can be recommended only for the weakest hardware platforms.

Questions, problems and solutions
The main problem of the Lamport scheme is, of course, an active malefactor ("man-in-the-middle"). Obviously, in the absence of server authentication to the client before sending a response, an attacker, sending allegedly more than the current value of the counter A 'on behalf of the server, can get the value H N-A' (P) from the client and then calculate any value from the range H N-A ' (P) ... H NA (P). The storage of the current value of the counter A for server control offered by some sources on the client does not actually solve the problem, because if we accept the threat of an intermediary attacker, then he is still able to intercept and suppress the correct client packet H NA (P ), authenticate with his help already from his station.
For the same reason, it does not make sense in this threat model to increase Counter A with any authentication request, regardless of whether it was successful or not, as suggested in some implementations. This scheme creates the threat of exhaustion (DoS) of the counter by the attacker and still does not protect against the attacker intermediary. The author himself in the original work does not recommend changing the counter in an unsuccessful attempt.
SSL (with one-way server authentication in front of the client) can provide optimal protection against both threats today. Once again, the “two-way” SSL with client authentication in front of the server with its certificates, of course, solves the whole problem of password theft in general. But it is an order of magnitude heavier both for deployment and for support with a large number of customers. Here, all the problems can be solved by the “one-way” SSL with a properly signed server certificate, which allows the client to report the next values of H K (P) only to the legitimate server.
There are certain problems with the Lamport scheme when restoring a server system from a backup if the recovery scheme implies an RPO greater than 0. In this case, the client’s successful authentications, overheard by the attacker, could potentially go through the “lost” period of time, and the counter value A recovered from the backup to dictate to the server to submit the previously observed A. value in the request again. Lamport himself suggests, in the case of restoration from the backup, to increase A by the average expected number of events a authentication for the time the system is offline, with some margin.
Reinitialization
And the last problem of the scheme: what to do when the counter of authenticated authentication A approaches the value of N? This situation is called reinitialization. In the original version of Lamport, the reinitialization implies a complete regeneration of the authentication information, that is, the replacement of P on the client side and H N (P) on the server side. If P is generated from a user password, respectively, either the hash amount needs to be entered, in addition to the server name, also the rekey initialization sequence number rekey_id: P = H (password || servername || rekey_id), store it on the server and inform the client in each request . Or, with each reinitialization, change the user's password and in any way ensure the complete non-repeatability of passwords, which seems to me a more difficult technical task. By the way, to protect against an attack on a password using a known P, it is not bad to re-initialize it at least 1 step before the Nth authentication, so that the client does not have to send the value P via an open channel.
Over the last 7-8 years, several more modern works on self-initializing hash chains have been published (they can be found in the search for the terms “re-initializable hash chains”, “infinite hash chains” or “self-updating hash chains”). However, I want to say that the mathematics there is very, very nontrivial, which is why the beauty of the idea of Lampert comes down almost to nothing.
Finally, if counter A increases (as in the original version) only after successful authentication, and clients have sufficient computing power, then re-initialization can be avoided altogether by simply setting N equal to, say, 100,000 (for 30 years with 10 authentications per day) that seems to me the most sensible solution.
In general, the Lamport scheme is a viable and much simpler alternative to asymmetric client authentication, which is somewhat unreasonably forgotten today.
Source: https://habr.com/ru/post/120657/
All Articles