Good day, Habr! Today I would like to tell you about greedy algorithms.

There are many methods for solving various tasks: dynamic programming , enumeration . No less well-known and fairly common are greedy algorithms.

I think every programmer in his life wrote a greedy at least once, perhaps without even thinking about it. What is it? Welcome under cat.

Greed is not a vice

So, the greedy algorithm (greedy algorithm) is the algorithm that makes the best choice locally at every step in the hope that the final solution will be optimal.
For example, Dijkstra's algorithm for finding the shortest path in a graph is quite greedy, because at every step we are looking for a vertex with the lowest weight, in which we have not yet been, after which we update the values ​​of other vertices. Moreover, it is possible to prove that the shortest paths found at the vertices are optimal.
')
By the way, the algorithm of Floyd , who is also looking for the shortest paths in the graph (albeit between all vertices), is not an example of a greedy algorithm. Floyd demonstrates another method - the dynamic programming method.

Using the greedy algorithm is pretty standard. Consider it on the example of the following task:

Schedule task

Let the freelance programmer Vasya Pupkin be given n tasks. Each task is known for its deadline, as well as its cost (that is, if he does not fulfill this task, then he loses so much money). Vasya is so cool that he can do one task in one day. The job can be started from the moment 0. It is necessary to maximize the profit.

A classic example of the use of the greedy: Vasya is profitable to do the most "expensive job", and the least expensive can not be done - then the profit will be maximum. The question arises: how to distribute tasks? We will sort through the tasks in descending order of cost and fill out the schedule as follows: if there is at least one more free space in the schedule before the order, then we’ll put it on the last of these places, otherwise we can’t fulfill it in time, then put in the end of the empty seats.

It turns out the following code:

//tasks -
Arrays.sort(tasks); //
TreeSet<Integer> time = new TreeSet<Integer>();
for ( int i = 1; i <= n; ++i) {
time.add(i);
}
int ans = 0;
for ( int i = 0; i < n; ++i) {
Integer tmp = time.floor(tasks[i].time);
if (tmp == null ) { // ,
time.remove(time.last());
} else { // ,
time.remove(tmp);
ans += tasks[i].cost;
}
}



When can you be greedy?

Sometimes it is sometimes tempting to use a greedy person wherever possible, but for some tasks this is unacceptable. For example, the task of a backpack : a thief made his way to a warehouse in which three things weighing 10 kg, 20 kg and 30 kg and costing 60, 100 and 120 wooden evergreen nanorubbles, respectively, are stored. A thief can take a maximum of 50 kg. It is necessary to maximize the profit of a thief. If you get greedy here and choose the most valuable thing (that is, 6 nano rubles per kg of the first piece, 5 nano rubles per kg of the second and 4 nano rubles per third kg), then the thief should take the first thing anyway, then there will be a place for the second thing, however, the optimal solution is the second and third thing.

Conclusion: if you are going to rob something, then take a truck with you. there is a field of applicability of greedy algorithms. There are no general recipes here, but there is a rather powerful tool with which you can determine in most cases whether the greedy will provide the best solution. Called matroid.

Life is not a matroid, life is a state machine!

As Wikipedia suggests, a matroid is a pair (X, I), where X is a finite set, called the carrier of a matroid , and I is a set of subsets of X, called a family of independent sets . The following conditions must be met:

1. 
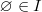
   The set I is non-empty. Even if the initial set X was empty - X = Ø, then I will consist of a single element — a set containing an empty one. I = {{Ø}}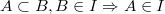
   
2. 
   Any subset of any element of set I will also be an element of this set.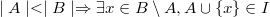
   
3. 
   If sets A and B belong to set I, and it is also known that size A is smaller than B, then there exists some element x from B that does not belong to A, such that the union of x and A will belong to set I. This property is not quite trivial , but most often the most important of all the others.
   

A matroid is called weighted if there is an additive weight function w on the set X. The weight of a set will be defined as the sum of the weights of its elements.

Let us return to our sheep as a freelance programmer with assignments. Here you can see the following matroid: let the carrier be a lot of tasks, and independent sets - successfully completed tasks. The weight of each application, let it be its cost. Check if this pair is a matroid:

1. the first property is obviously satisfied. An empty set of completed tasks is included in our set. Well, do not care that Vasya does not want to make money.
   
2. the second set is also satisfied. Why this is so: let's sort the successfully completed tasks in the order of increasing the deadline. In this order, they will still be successfully executed. In this order, it is obvious that any subset of successfully completed tasks will be successfully completed.
   
3. the third property, though not obvious, but fulfilled. Suppose we have two sets of successfully completed tasks A and B, and it is known that | A | <| B |. Standardly sort the tasks in order of increasing the deadline in both sets. Take the task from B, which is not in A, and try to add it to the set A. We will succeed, because if A did not have a space, then this task should have been present.
   

Why am I doing this? The beauty of matroids lies in the Rado-Edmonds theorem: if you prove that an object is a matroid, the greedy algorithm will work correctly and will produce the correct result.

By itself, the greedy algorithm is implemented like this:

// sort by weight
// first the answer will be an empty set
for to
if 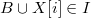then // if appropriate
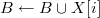// this is included in the set

Bibliography

• Wikipedia
  
• Discrete Mathematics: Algorithms
  
• Kormen
  

PS

By the way, the schedule problem can be solved faster in O (n) . Who is not weak? (Hint: you need to replace the treeset with a different structure).