Ultra fast image markup

In the article I will tell you how to quickly list connected objects on a binary raster, much faster than I mentioned in the previous article . It would seem, where such speed; now we will be “cracking down” with pictures of 4096 by 4096 for tens of milliseconds. And although the task is interesting in and of itself, but its solution is based on a fairly simple and original method with fairly wide applicability, the main thesis of which is “let's make it as simple as possible and see what happens”. In this case, CUDA will be used as the main calculator, but without special specifics, because we want to make it “very simple”.

Task

It is necessary to select all the connected objects on the binary raster (the colors of the pixels are only black and white) and somehow mark them. For clarity, we will mark in different colors. Of course, the correspondence “color - object index” is rather trivial. In our case, two points are connected if they are direct neighbors vertically or horizontally (four-connected), but the algorithm can easily be modified for the eight-connected case (this is not the main thing). Very clearly the problem is presented in this article .

For example, the original picture:


The algorithm will work with very large images (up to 16384x16384), but for understandable reasons, thumbnails will be used throughout the article.
')

To explore or not?

It is quite reasonable, when getting a new task, to think about what method of solving it would be optimal, what limitations may arise in the way of solving, what is the labor-intensive solution. In order to be objective when choosing a method, you need to consider many options, sometimes “too many”, so the main thing is to start the reasoning correctly in order to weed out unnecessary options faster.

Worst "best case"

Obviously, to solve the problem, you need to consider each pixel of the image. Let's see how long the model code will be executed on the image of size 8192x8192:

for ( int x = 0; x < dims[0]; x++)
{
for ( int y = 0; y < dims[1]; y++)
{
image[x + dims[0]*y] = 0;
}
}


Yes, it can be significantly “optimized” by rolling the cycle into one, but any reasonable method implies the ability to access individual pixels of the image, so the indexing is intentionally left. Run it on some “mediocre” processor (in my case - Core 2 Duo E8400) and get the operating time around 680-780 ms .

It is difficult to say whether this is a lot or a little, but it seems that the task will not be solved faster.

Or so it only seems; because “all means are good” and there are technologies that greatly simplify the solution of the problem and give the best results; and in this case, CUDA technology, which has very good indicators for memory intensive tasks, can help us a lot.

On my average GTX460 video card, we get access speed to video memory of about 40 GB / s against 2 GB / s for main memory. This processing speed is achieved through the use of mass parallelism and fairly fast memory.

Divide and rule

Quite nontrivial may be the separation of the task when taking into account the specifics of computing on video cards: there is no stack, not very fast synchronization between threads, the inability to build complex data structures.

A reasonable way to divide the original image seems to divide it into small "squares", each of which will be processed by a separate stream; it fits well with the CUDA computing model. And if you omit unnecessary specifics (which is done by a single transformation):

UID = threadIdx.x + blockDim.x * blockIdx.x

Then we get that the original task is represented as a combination of the results of the execution of subtasks for all unique identifiers of flows (UID). Yes, we still do not know what we are going to do, but we already know how to break the task.

So (the riot of colors is the author's style, and the gradient shows that all UIDs are different) we can cover the original image:


Each stream will process the pixels within the corresponding block, with a size of, for example, 32 x 32. Then, some synchronization and merging of the results may be required.

Easy peasy

One remarkable principle is often used in mathematics: “if something is impossible, but you really want it, then it is possible”, in fact it’s just “pushing” the complications “for later”, but in this case it will be very useful to us.

Let us take the simplest algorithm for the fill and within each block, apply it to the corresponding points (starting with each not yet filled), without thinking about the boundary effects at all.

In essence, we fill in the image points that are in the block with its unique identifier, the result is predictable:



While we started each new iteration of the fill for the same UID with the same “color”. But this makes little sense - if we are not able to ensure that with this approach we can fill the connected (in the original picture) areas with one color, then at least we can fill the disconnected areas with different “colors”. Therefore, we will perform each new iteration of the fill with a new color obtained from the UID and a special additive that guarantees the uniqueness of this color in the overall picture (it is enough to add the total number of streams multiplied by the iteration number).



Understand that we won more easily in the picture with the “grid” denoting the boundaries of the processed squares:



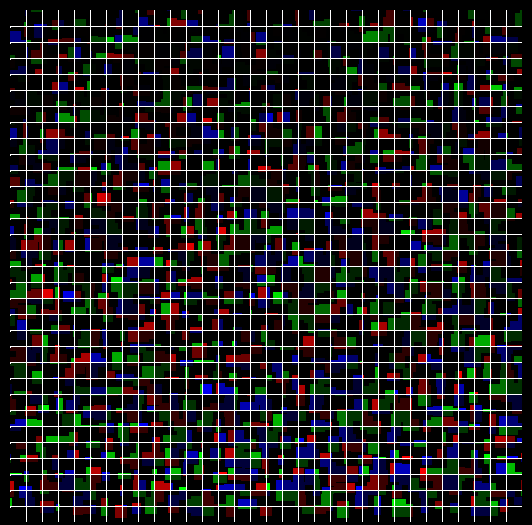
Now, within each square, the connected regions are filled with the same color, the disconnected - with different colors. It will work for O (n ^ 3) (yes, I chose the worst implementation of the fill algorithm) for each square, which are all (imageSize.x / n) * (imageSize.y / n), most of which will be processed simultaneously with sufficient the number of threads (usually about 256).

Deferred difficulties

It remains to collect the results in one. Although at the level of awareness it’s more difficult than using the classical method for subtasks, it is algorithmically much faster.

In fact, we want to understand what different colors belong to the same connected area.

To do this, just go through the pixels of the grid (exactly the one that is drawn in white in the illustration) and check whether the pixels of different colors are immediate neighbors. If they are, then both colors denote essentially one object, which we can easily “repaint”, or keep this fact “in mind” (usually, to get the parameters of objects, this is enough).

Simple arithmetic leads to the fact that the number of grid pixels linearly depends on the perimeter of the image - we do not need to process all the points inside the squares, but only their border is needed.

After passing through these points, you can create a color map (c ₁ == c ₂ == c ₃ ...) and accurately draw the result:

Implementation and speed estimates

Surprisingly, the “bottleneck” of this method is the transfer of data from main memory to video memory, here we have no alternatives:

START_ACTION( "Allocating GPU memory: image... " );
unsigned int * data_cuda;
cutilSafeCall( cudaMalloc(( void **)&data_cuda, data_cuda_size) );
END_ACTION(data_cuda_size);

START_ACTION( "Copying input data to GPU memory: image... " );
cutilSafeCall( cudaMemcpy(data_cuda, image, data_cuda_size, cudaMemcpyHostToDevice) );
END_ACTION(data_cuda_size);


The resulting 2 GB / s is no surprise - this is the speed of access to RAM. For images with which we work - it's milliseconds, not scary.

Calling the kernel (the function that is performed on the video card):

START_ACTION( "Calling CUDA kernel... " );
cutilSafeCall( cudaThreadSynchronize() );
processKernelCUDA<<<GRID, THREADS>>>(data_cuda, dims[0], dims[1]);
cutilSafeCall( cudaThreadSynchronize() );
END_ACTION(data_cuda_size);


The output speaks for itself:

Calling CUDA kernel... 26.377720 msecs.
Throughput = 2.36942 GBytes/s

In fact, it was possible to implement the execution of all subtasks, in less time transferring the necessary data (images) to the video memory. This is despite the fact that I chose the worst fill algorithm, and did not implement its optimal implementation. Does it make sense to optimize something? You decide :)

Without the kernel code, the presentation will probably not be complete, so please love and favor:

__global__ void processKernelCUDA(unsigned int * image, int dim_x, int dim_y)
{
// Full task size: image dimensions
int TASK_SIZE = dim_x * dim_y;

// Max UID for full task (really count of 'quads')
int MAX_UID = TASK_SIZE / QUAD_SIZE / QUAD_SIZE;

// calculate UID by CUDA implicit parameters; WORKERS = GRID*THREADS
for ( int UID = threadIdx.x + blockDim.x * blockIdx.x; UID < MAX_UID; UID += WORKERS)
{
// count of quads for x-dimension
int quads_x = dim_x / QUAD_SIZE;

// current quad index form UID
int curr_quad_x = UID % quads_x;
int curr_quad_y = UID / quads_x;

// offset in global task
int offset = curr_quad_x * QUAD_SIZE + dim_x * curr_quad_y * QUAD_SIZE;

// id of 'color' to mark block, have to be >= 2
int COLOR_ID = 2 + UID;

do
{
// means that fill is not started yet
bool first_shot = true ;

// process quad starting with specified 'offset'
bool done_something;

do // fill step
{
done_something = false ;
for ( int local_y = 0; local_y < QUAD_SIZE; local_y++) // step by y
{
// calcluate point index in whole image
int start_x = offset + local_y * dim_x;
for ( int pos = start_x; pos < start_x + QUAD_SIZE; pos++) // step by x
{
if (image[pos] == 1) // is not marked with ID, is not blank
{
if ( first_shot /* start fill */ // else check neighbors:
|| image[pos-1] == COLOR_ID // x--
|| image[pos+1] == COLOR_ID // x++
|| local_y > 0 && image[pos-dim_x] == COLOR_ID // y--
|| local_y < QUAD_SIZE && image[pos+dim_x] == COLOR_ID ) // y++
{
image[pos] = COLOR_ID; // mark with ID
first_shot = false ; // fill already started
done_something = true ; // fill step does something
}
}
}
}
} while (done_something); // break if fill have no results

if (first_shot)
{
// no more work in this block, exit
break ;
}
else
{
// next iteration: restart block with different color ID
COLOR_ID += MAX_UID;
}
} while ( true );
}
}



The input is a pointer to the image and the resolution of the image in X and Y. Inside, the subtask's identifier is calculated, the offset of the square corresponding to the subtask is selected, and it begins to fill with a non-recursive fill algorithm.

The secret of success

Of course, there are not so many tasks that are solved in less time, the time for obtaining data for them, but in this case it’s lucky. And besides luck - the right choice of technology for the solution and the right way of reasoning, which allowed to get a result (sort of) of a rather serious task in less than a working day.

PS A big request, do not copy the pictures and do not re-publish without my permission (I am the author of the method).