Recognition of handwritten mathematical expressions
Hello, Habr!
In this article I want to share handwriting recognition of mathematical expressions. Although there are already such handwriting recognition tools such as the Mip.exe “Math Input Panel” in Windows7, the variety of approaches to solving this problem is impressive. I am going to tell about one of these approaches.

')
Recognition of mathematical expressions is a more complicated type of recognition than of character recognition, since besides recognition of a mathematical symbol itself, it is also necessary to recognize the structure of a mathematical expression.
In the online recognition of handwritten mathematical expression usually distinguish the following stages:
Over the decades of research in the field of recognition of mathematical expressions, a huge number of algorithms and theories have been invented. I will tell you about a simple approach, which, nevertheless, gives a good result. He assumes that stages 1, 2 and 3 work together, and the output gives a list of characters that is recognized as a mathematical expression in stage 4.
The first step is to collect and pre-process data. A training set for a particular class of characters consists of a set of characters. A symbol is an ordered set of strokes, and a stroke is an ordered set of pairs (x, y), where the first pair corresponds to the tangency point of the pen, and the last pair to the tear-off point. Each character is drawn by a certain number of strokes in a certain order.
The purpose of preprocessing is to convert the raw data of the patterns into a format that allows you to create a character model for further classification. To simplify the model, it is necessary to remove the information that is not needed in the classification. The initial set of strokes is converted into a vector of a certain and rigidly fixed dimension.
Scaling, shifting and changing the number of control points
Each point of each stroke shifts so that the starting point is the upper left corner of the symbol bounding box. After that, all points are scaled while preserving the ratio of width to height so that the symbol fits inside the square. Further, the set of points of each stroke is changed so that the points are located equidistantly (resampling along the arc length using the linear interpolation method). The number of points is fixed and equal to 36 / N, where N is the number of strokes in a symbol (36 is divided into 1, 2, 3 and 4, where 4 is the maximum number of strokes in one symbol).
Finally, the coordinates of the points are assembled into a single vector of 72 elements, where the first 36 elements represent the x coordinates, and the last ones represent the y coordinates.
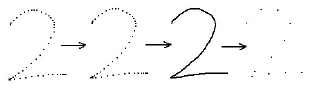
What did we get?
And we got a set of vectors of the same dimension, where each class of symbols corresponds to a certain number of vectors. This information can be used, for example, to train a neural network, or to recognize a character using the k-nearest-neighbor algorithm.
In fact, the dimension of the vector can be reduced several times, without losing almost any information. This algorithm is called the “Principal Component Method”.
As a result, the following something was created to train the classifier:
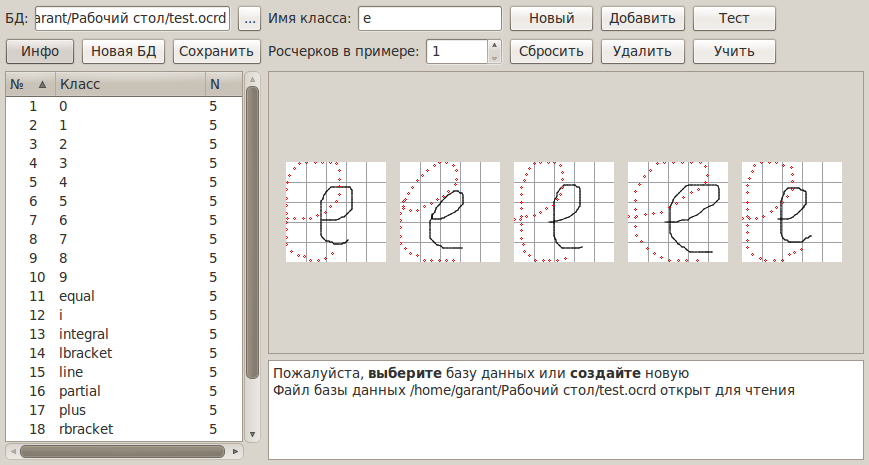
The categorizer recognizes characters individually. However, when it is necessary to recognize streaming input, it cannot know in advance which strokes make up a character, and how many characters have been entered. Consequently, the capabilities of the classifier must be supplemented by determining the number and location of the symbols of the expression. The solution to this problem is equivalent to the best grouping of strokes into symbols, called expression segmentation.
Suppose that the entered strokes are ordered by time, that is, when a character consisting of three strokes is entered, the strokes of this symbol are sequentially entered. For example, it is not allowed to put a dot above the i character after writing the characters that follow i . Given this assumption, in order to define symbols consisting of several strokes, it is necessary to consistently consider the groups of strokes, ranging in size from 1 to N (N in our case is 4). If a symbol from several strokes is recognized by the classifier with an error less than a certain threshold, then this symbol is preferred. The number of considered combinations is equal to F (N) = O (kN) . If none of the classification results exceeds the threshold value, the threshold value is increased and the step is repeated, or a recognition error occurs.
It should be noted that some symbols that cannot be recognized as different (for example, minus signs and fractions) are designated as one symbol (horizontal bar), which is renamed during structural analysis.
The segmentation algorithm can be improved by defining valid characters for each number of strokes. Thus, two strokes cannot be recognized as a symbol consisting of one or three strokes.
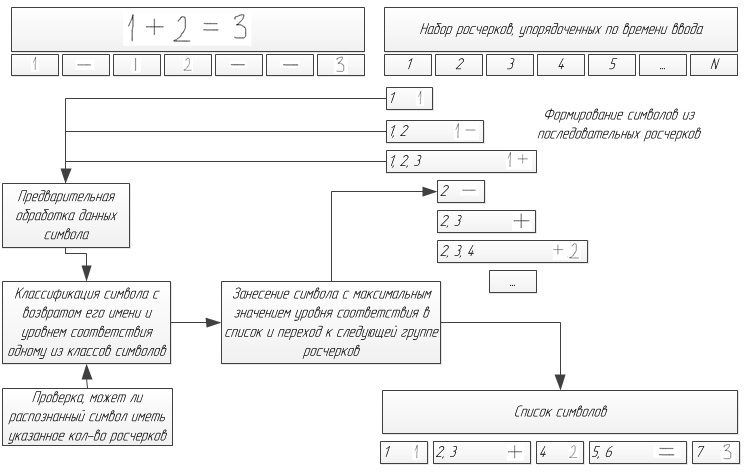
Also, when implementing this algorithm, in order to prevent possible segmentation errors, an interface is needed to instantly correct an incorrect result, or to cancel the input of the last character.
Ambiguity resolution
The qualifier cannot know whether we have entered the minus symbol or the fraction symbol. This requires additional verification. So, at a certain distance up and down from the trait of the “minus” symbol, no strokes will be located, and the “fractions” symbol will be located. Based on this, the character of the “dash” is renamed to the “minus” or “fraction” symbol, respectively. Almost the same - with a decimal point and a multiplication sign.
Now, finally, let's move on to recognizing the structure of the expression :-)
Character areas and attributes
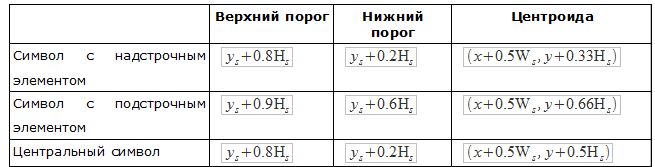
Relationships of mathematical operators are determined depending on the position and relative size of the character in the expression. For definition of relations, spatial areas are used “top left”, “top”, “superscript”, “subscript”, “bottom”, “bottom left” and “subexpression”. For example, it is expected that the operands (numerator and denominator) of the horizontal line (fraction operator) will lie in the “top” and “bottom” areas relative to the horizontal line
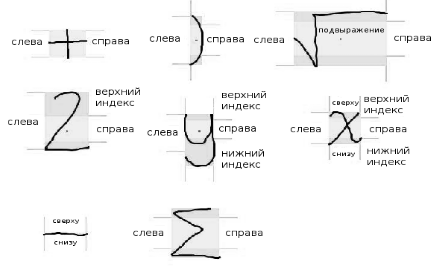
Based on simple attributes (upper bound, right bound, etc.), you can determine the threshold of the upper index, the threshold of the lower index and other attributes. These are numerical attributes that are used to separate areas around a symbol. Also, based on simple attributes, you can determine the center point.
The center point is the point that determines the location of the symbol in any of the areas. To determine the attributes of a character, a character is classified as an asterisk, with a descriptor, or central.
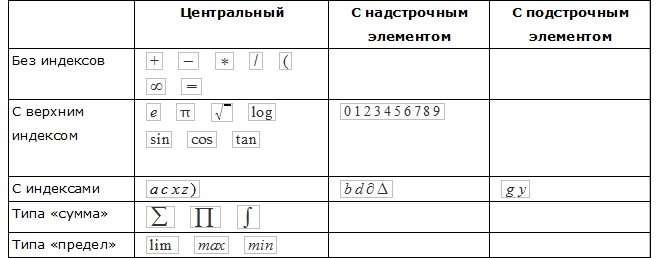
Each character class has attributes that are defined differently. This is necessary in order to avoid ambiguities in the structural analysis:
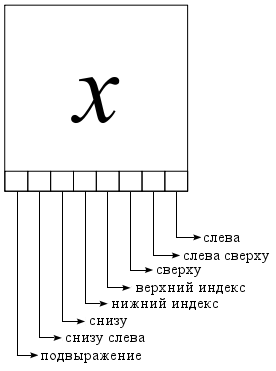
Baseline Expression
The baseline is a list that represents the horizontal arrangement of characters in an expression. Each symbol has links to other baselines that satisfy different spatial relationships.
Dominance of characters and the dominant baseline
Dominance is defined as follows: the symbol s dominates the symbol a, if a lies in the domain s, and s does not lie in the region a. However, both symbols may lie in each other's areas. As a result, the calculation of the
If you have an ordered list of L characters, you can determine the leftmost dominant character in the list by performing the following recursive procedure:
The dominant expression baseline is the baseline to which no symbol refers. While reading a mathematical expression, it is usually first to search for the leftmost dominant character, then the next dominant character, and so on, until all the characters of the baseline are found.
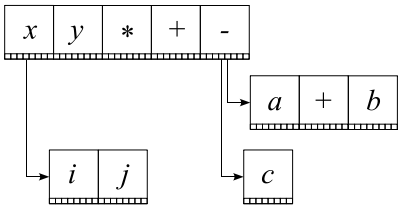
The data structure that represents the expression is called the baseline tree. Suppose we have an expression

Then the baseline tree of this expression will look like this:
The dominant baseline Db is constructed using the following function:
The baseline tree is created by recursively finding the dominant baselines in an expression described by an ordered list of characters L.
The resulting tree is a structure of a mathematical expression, and it can be converted into the code of a formula editor by parsing it. In my case, this is an OpenOffice editor.
AndGLaDOS turned out to be an application from this algorithm, which, although not without its ability to make mistakes in recognizing individual characters, can recognize quite complex mathematical expressions on the fly. This is how it looks like:

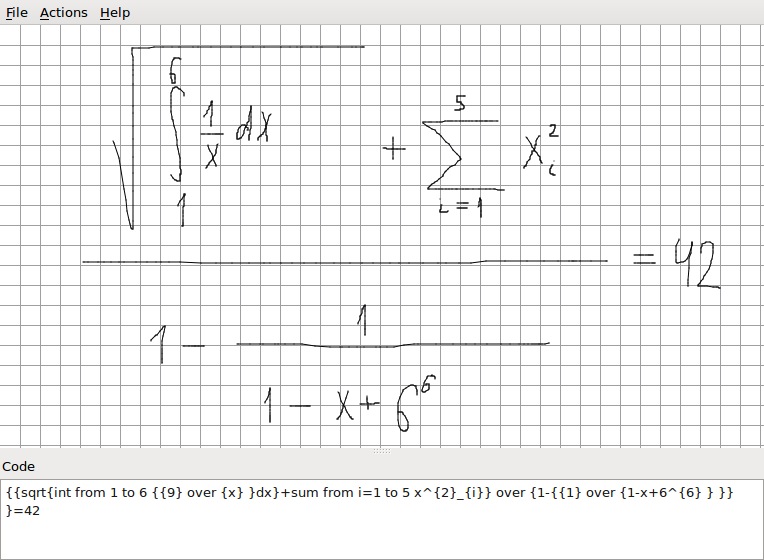
And it can recognize, though sometimes not without errors, these are the formulas (and whoever finds the first character recognition error is the good fellow :-)
That ended my first article on Habré. I hope she was not very boring, and will be useful to someone! Thank you for attention!
Literature:
In this article I want to share handwriting recognition of mathematical expressions. Although there are already such handwriting recognition tools such as the Mip.exe “Math Input Panel” in Windows7, the variety of approaches to solving this problem is impressive. I am going to tell about one of these approaches.
')
Small introduction
Recognition of mathematical expressions is a more complicated type of recognition than of character recognition, since besides recognition of a mathematical symbol itself, it is also necessary to recognize the structure of a mathematical expression.
In the online recognition of handwritten mathematical expression usually distinguish the following stages:
- Collection and preliminary processing of data:
- Splitting an expression into characters (expression segmentation):
- Recognition of individual characters:
- Recognizing the structure of a mathematical expression:
Over the decades of research in the field of recognition of mathematical expressions, a huge number of algorithms and theories have been invented. I will tell you about a simple approach, which, nevertheless, gives a good result. He assumes that stages 1, 2 and 3 work together, and the output gives a list of characters that is recognized as a mathematical expression in stage 4.
Collection and preliminary processing of data
The first step is to collect and pre-process data. A training set for a particular class of characters consists of a set of characters. A symbol is an ordered set of strokes, and a stroke is an ordered set of pairs (x, y), where the first pair corresponds to the tangency point of the pen, and the last pair to the tear-off point. Each character is drawn by a certain number of strokes in a certain order.
The purpose of preprocessing is to convert the raw data of the patterns into a format that allows you to create a character model for further classification. To simplify the model, it is necessary to remove the information that is not needed in the classification. The initial set of strokes is converted into a vector of a certain and rigidly fixed dimension.
Scaling, shifting and changing the number of control points
Each point of each stroke shifts so that the starting point is the upper left corner of the symbol bounding box. After that, all points are scaled while preserving the ratio of width to height so that the symbol fits inside the square. Further, the set of points of each stroke is changed so that the points are located equidistantly (resampling along the arc length using the linear interpolation method). The number of points is fixed and equal to 36 / N, where N is the number of strokes in a symbol (36 is divided into 1, 2, 3 and 4, where 4 is the maximum number of strokes in one symbol).
Finally, the coordinates of the points are assembled into a single vector of 72 elements, where the first 36 elements represent the x coordinates, and the last ones represent the y coordinates.
What did we get?
And we got a set of vectors of the same dimension, where each class of symbols corresponds to a certain number of vectors. This information can be used, for example, to train a neural network, or to recognize a character using the k-nearest-neighbor algorithm.
In fact, the dimension of the vector can be reduced several times, without losing almost any information. This algorithm is called the “Principal Component Method”.
As a result, the following something was created to train the classifier:

Segmentation and recognition of individual characters
The categorizer recognizes characters individually. However, when it is necessary to recognize streaming input, it cannot know in advance which strokes make up a character, and how many characters have been entered. Consequently, the capabilities of the classifier must be supplemented by determining the number and location of the symbols of the expression. The solution to this problem is equivalent to the best grouping of strokes into symbols, called expression segmentation.
Suppose that the entered strokes are ordered by time, that is, when a character consisting of three strokes is entered, the strokes of this symbol are sequentially entered. For example, it is not allowed to put a dot above the i character after writing the characters that follow i . Given this assumption, in order to define symbols consisting of several strokes, it is necessary to consistently consider the groups of strokes, ranging in size from 1 to N (N in our case is 4). If a symbol from several strokes is recognized by the classifier with an error less than a certain threshold, then this symbol is preferred. The number of considered combinations is equal to F (N) = O (kN) . If none of the classification results exceeds the threshold value, the threshold value is increased and the step is repeated, or a recognition error occurs.
It should be noted that some symbols that cannot be recognized as different (for example, minus signs and fractions) are designated as one symbol (horizontal bar), which is renamed during structural analysis.
The segmentation algorithm can be improved by defining valid characters for each number of strokes. Thus, two strokes cannot be recognized as a symbol consisting of one or three strokes.
Also, when implementing this algorithm, in order to prevent possible segmentation errors, an interface is needed to instantly correct an incorrect result, or to cancel the input of the last character.
Ambiguity resolution
The qualifier cannot know whether we have entered the minus symbol or the fraction symbol. This requires additional verification. So, at a certain distance up and down from the trait of the “minus” symbol, no strokes will be located, and the “fractions” symbol will be located. Based on this, the character of the “dash” is renamed to the “minus” or “fraction” symbol, respectively. Almost the same - with a decimal point and a multiplication sign.
Now, finally, let's move on to recognizing the structure of the expression :-)
Pattern recognition
Character areas and attributes
Relationships of mathematical operators are determined depending on the position and relative size of the character in the expression. For definition of relations, spatial areas are used “top left”, “top”, “superscript”, “subscript”, “bottom”, “bottom left” and “subexpression”. For example, it is expected that the operands (numerator and denominator) of the horizontal line (fraction operator) will lie in the “top” and “bottom” areas relative to the horizontal line
Based on simple attributes (upper bound, right bound, etc.), you can determine the threshold of the upper index, the threshold of the lower index and other attributes. These are numerical attributes that are used to separate areas around a symbol. Also, based on simple attributes, you can determine the center point.
The center point is the point that determines the location of the symbol in any of the areas. To determine the attributes of a character, a character is classified as an asterisk, with a descriptor, or central.
Each character class has attributes that are defined differently. This is necessary in order to avoid ambiguities in the structural analysis:
Baseline Expression
The baseline is a list that represents the horizontal arrangement of characters in an expression. Each symbol has links to other baselines that satisfy different spatial relationships.
Dominance of characters and the dominant baseline
Dominance is defined as follows: the symbol s dominates the symbol a, if a lies in the domain s, and s does not lie in the region a. However, both symbols may lie in each other's areas. As a result, the calculation of the
dominates(s,a) function is performed as follows (each subsequent step is performed if it was not possible to determine which symbol dominates over which one in the previous one):- Check the geometric arrangement of characters.
- Check character class. For example, the fraction symbol will dominate the digit symbol.
- Check the relative size of the character
If you have an ordered list of L characters, you can determine the leftmost dominant character in the list by performing the following recursive procedure:
getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).getDominantSymbol(L): n = length(L) — . n==1, s(n) s(n) s(n-1) , s(n-1) L, s(n) getDominantSymbol(L).
The dominant expression baseline is the baseline to which no symbol refers. While reading a mathematical expression, it is usually first to search for the leftmost dominant character, then the next dominant character, and so on, until all the characters of the baseline are found.
The data structure that represents the expression is called the baseline tree. Suppose we have an expression
Then the baseline tree of this expression will look like this:
The dominant baseline Db is constructed using the following function:
constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
constructDominantBaseline(Db,L):
Db , Db = addSymbol(Db,getDomninantSymbol(L)) s = getLastSymbol(Db) Hs = getRightNeighbors(s,L) L, s Hs , Hs, sd = getDominantSymbol(Hs) Db = addSymbol(Db,sd) : constructDominantBaseline(Db,L)
The baseline tree is created by recursively finding the dominant baselines in an expression described by an ordered list of characters L.
ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
ConstructBaselineTree(L):
L , Db constructDominantBaseline(Db,L) Db, , s Db , , , L = Db , constructBaselineTree -, 5
The resulting tree is a structure of a mathematical expression, and it can be converted into the code of a formula editor by parsing it. In my case, this is an OpenOffice editor.
What came out of all this
And

And it can recognize, though sometimes not without errors, these are the formulas (and whoever finds the first character recognition error is the good fellow :-)

Epilogue
That ended my first article on Habré. I hope she was not very boring, and will be useful to someone! Thank you for attention!
Literature:
- Nicholas Matsakis. Recognition of handwritten mathematical expressions. Master's thesis, Massachusetts Institute of Technology, Cambridge, MA, May 1999.
- Ernesto Tapia: Understanding Mathematics: A Handbook for Mathematical Expressions, Berlin, 2004
- Eva Gallardo Perez: The 2D Grammar Extension of the CMP Mathematical Formula on-line Recognition System, 3, 2009
Source: https://habr.com/ru/post/120159/
All Articles