Counting objects in a binary image. Part 2

annotation

This article is written in the continuation of the first part of the article about working with binary images, which describes how to count objects. However, there is little confusion from a single count, often I want to know some geometrical parameters of recognizable objects. It seems that there is to count - I recognized the number of eights - the area is 19, I calculated the number of sevens - the area is 7 (see the picture in the Annotation).
Doing so, we will be forced to use an additional pass through the image, it is desirable to avoid this - in favor of increasing the efficiency of implementation. As planned, this topic describes how to calculate the geometric characteristics of objects without an additional pass.
And also: the form factor and the roses of Guido Grande and the difference between a square and a rectangle, and it is different from a star.

Previous parts of the article:
Part 1

Counting objects and calculating geometric features

At the very beginning we will deal with the area. In the previous article , 5 positions of the ABC-mask were considered, the fifth position included the merging of two marked-up connected areas, which turned out to be under different but equivalent numbers.
Add to the source code - in each of the conditional positions the following logic:

• For positions from 1st to 5th: they should increase the area of ​​the object with the current mark by one.
• For the 5th position, in addition, when regions are combined under equivalent numbers B and C, we perform S (B) = S (B) + S S.

For brevity, I will give the source script code only with new lines in each of the positions.

if A == 0 then
elseif B == 0 & C == 0 then
/.../
Squares (cur) = Squares (cur) + 1;
elseif B ~ = 0 & C == 0 then
/.../
Squares (B) = Squares (B) + 1;
elseif B == 0 & C ~ = 0 then
/.../
Squares © = Squares © + 1;
elseif B ~ = 0 & C ~ = 0 then
Squares (B) = Squares (B) + 1;
if B == C then
Im (i, j) = B;
else
/.../
Squares (B) = Squares (B) + Squares ©;
Squares © = 0;
end
/.../
end
* This source code was highlighted with Source Code Highlighter .

Listing 1 - Changes in the script code for calculating the area of ​​marked objects.
')
Counting the perimeter of the object is a little more complicated. As in the situation of area if B == 0 or C == 0
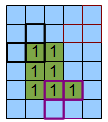
we also need to increase the perimeter. However, this will not be enough. Let us introduce another ABC mask, the same corner (black mask in the figure), but inverted by 180 degrees (purple mask in the figure). This will add to us three more possible situations, but they should be considered only within the framework of position number 5.

elseif B ~ = 0 & C ~ = 0 then
Squares (B) = Squares (B) + 1;

if B == C then
Im (i, j) = B;
else
Im (i, j) = B;
Im (Im == C) = B;
Squares (B) = Squares (B) + Squares ©;
Squares © = 0;
Perimetrs (B) = Perimetrs (B) + Perimetrs ©;
Perimetrs © = 0;
end

A = Im (i, j);
kn = j + 1;
if kn> n then
kn = n;
B = 0;
else
B = Im (i, kn);
end

km = i + 1;
if km> m then
km = m;
C = 0;
else
C = Im (km, j);
end

if B == 0 & C == 0 then
Perimetrs (A) = Perimetrs (A) + 1;
elseif B ~ = 0 & C == 0 then
Perimetrs (A) = Perimetrs (A) + 1;
elseif B == 0 & C ~ = 0 then
Perimetrs (A) = Perimetrs (A) + 1;
end

end
* This source code was highlighted with Source Code Highlighter .

Listing 2 - Changes in the script code for counting the perimeter of the object.

Summarizing this principle, it can be argued that using the ABC mask and object marking algorithm, any geometric signs that have the property of linearity when merging regions can be calculated, that is, let object 3 consist of two parts: Obj3 = Obj1 + Obj2, then its sign F (Obj3) = F (Obj1) + F (Obj2). An example of this could be the center of gravity of an object.

Form factor

From school, we all know that for any geometric figure you can calculate the area and perimeter. For example, for a circle, the formulas look like

Consider the interesting relationship (3), which binds in itself both the area and the perimeter - this is one of the types of form factors. Substituting into it the appropriate formulas for the area and perimeter of a circle, it is easy to understand that for circles of any radius the form factor is 0.
However, everything is quite simple for a circle, but what about more complex shapes? In the article we will look at the so-called Guido Grande roses (Figure 1).

Figure 1 - The set of Guido Grande roses.

For ease of implementation, so as not to get involved in the polar coordinate system, I redid the initial formulas for Cartesian coordinates (4), but they are not equivalent to the initial construction rules, but the result is similar and suitable for our purposes (Figure 1).

How does the form factor (3) behave depending on the variable parameter of the rose? This is demonstrated in the graph in Figure 2.

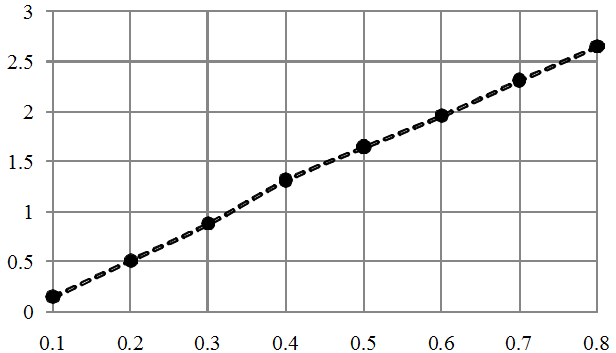
Figure 2 - Form factor (3) of the Guido-Grandi rose along the horizontal axis depending on the variable parameter along the vertical axis.

A linear relationship becomes obvious; I am sure that it has an analytical record and the formula for this can be derived quite easily. but let it be a little puzzle for readers.
As a result, using a simple relationship between the area and the perimeter, we received a sign by which to identify the figure - to recognize. In practice, this feature is only one of many in the feature vector. Since it is even resistant to homothety distortions (similarity, scale), but due to errors in the contour of the figure generated by binarization and quantization, it is calculated with an accuracy of + (-) 0.15, while varying the radius of the rose.

Now let's see how to distinguish squares and rectangles using this attribute. For brevity, only an illustration is shown - Figure 3.

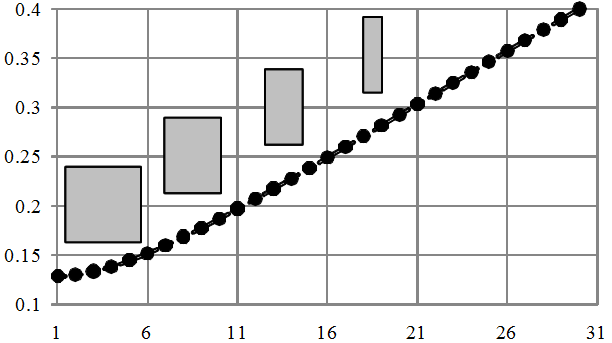
Figure 3 - Changing the form factor when extruding a square into a rectangle.
Here the dependence is already non-linear, it is obvious from the analytical formula.

There are many similar heuristic factors of the form, which include the compactness of the figure.

Conclusion

Here you can download the SciLab script for your experiments, which includes:

• Construction of the contour of stars.
• Fill using the algorithm from this article.
• Marking and counting area and perimeter.
• Calculation of the form factor.

The archive is encrypted with the password, which is specified in the first comment, I apologize for such inconveniences, but this is for the purpose of protection from copy-pasters, which, as a rule, do not copy comments.

Thanks to all who read, waiting for your comments. If someone is familiar with the literature where form factors are described, I ask you to give references, I could not find anything before publication in order to have self-criticism.

UPD: 06/06/11 15:28