Recursive zip archive
Many habra users are probably familiar with quinees - programs that display their own source code. Today I want to show how to make an interesting version of Quine - ZIP-archive, which is unpacked into itself .
')
The algorithm used in ZIP files ( Lempel-Ziv ) is actually quite simple. There are two types of instructions in it:
Accordingly, our task is as follows: using this algorithm to write a program that displays its code at startup. In other words, write a compressed data stream that unfolds into itself. Maximum program: write a stream that unfolds into itself with arbitrary data at the beginning and end (so that it can be used as a real zip or gzip file, with a header and other necessary data).
Let's agree to use
A simple quine will look like this:
(It can be seen that the contents of the “Code” and “Output” columns are the same)
The interesting part of the program is a sequence of 6 bytes
If we write quine on Python, usually the problem is that the
(The output is the code plus
I had to spend most of Sunday to get to this point, but when I did it, I already knew that I had won. From my experiments, I found out that it is quite easy to create a program that outputs itself without several instructions, or even one that displays itself with a prefix, minus several instructions. The extra bytes
This is how a program with arbitrary prefix and suffix looks like:
(The output is P, then the bytes from the “Code” column, then S.)
Now go to the real action. We solved the main technological problem of creating a recursive zip file, but there are still a few details left.
The first problem: to translate our quine, recorded in the simplified opcodes, into real Lempel-Ziv opcodes. RFC 1951 defines the DEFLATE format used in gzip and zip; a sequence of blocks, each of which contains a sequence of opcodes encoded by Huffman coding. Huffman coding assigns strings of different lengths to different opcodes, which does not coincide with our assumption that opcodes have the same length. But wait! We can, if we try, find a fixed length coding that can be used.
There are literal blocks and opcode blocks in DEFLATE. The header of the literal block is 5 bytes:

If our opcodes L occupy 5 bytes each, opcodes R must also occupy 5 bytes, and each byte above will be repeated five times (for example, the argument for L4 now takes 20 bytes and R4 repeats the last 20 bytes of output). The block of opcodes with one

Fortunately, the opcode block containing two instructions

Coding a

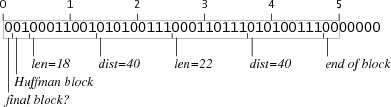
A block that repeats the last 10 bytes is 2 bits less than needed, but each block of repetition is followed by a block of literals that starts with three zero bits and is added to the border of the nearest byte. If the repeat block ends 2 bits before the boundary and a literal block follows, the fill-in will insert the missing two bits. In the same way, a block repeating 40 bytes goes out over the border by 5 bits, but these bits are zero. Starting block 5 bits later, we subtract these bits from the dobivka. Both of these tricks work because the last 7 bits of any repeat block are zero, and the bits in the first byte of the block of literals are also zero, so the border is not visible. If the literal block began with one bit, this cunning device would not have worked.
The second obstacle is that the zip archives (and gzip too) store the checksum of uncompressed data. Since uncompressed data is the same zip archive, the checksum is also involved in the calculation. So, we need to find such a value of
The CRC32 command interprets the entire file as one large number and calculates the remainder when this number is divided by a specific constant using a special division method. We could write the corresponding equations and solve them for
If you want to repeat all this on your own, a couple of simple problems await you, for example, make the length of the tar file share without a balance by 512 and compress the zip header to 59 bytes so that
So, I got the files r.gz (gzip-archive), r.tar.gz (tar-file, compressed gzip), and r.zip (zip-archive). It is a pity, but I could not find a program that would recursively unpack these files to infinity. It would be fun to watch, but it looks like much less complicated zip-bombs have already spoiled us all the fun.
If you feel fit, here is rgzip.go , a Go program that generates these files. I wonder if you can create a zip file containing a gzip file containing the original zip file in turn). Ken Thompson suggested trying to create a zip-archive, unpacking his copy but slightly larger in size, so that when recursively unzipping the archive size grew indefinitely (if you succeed in one or the other, please leave a comment).
Lempel-Ziv algorithm
')
The algorithm used in ZIP files ( Lempel-Ziv ) is actually quite simple. There are two types of instructions in it:
literal(n) , followed by a stream of data that should be output as is, and repeat(d, n) , which returns back to d bytes and outputs n bytes from this position.Accordingly, our task is as follows: using this algorithm to write a program that displays its code at startup. In other words, write a compressed data stream that unfolds into itself. Maximum program: write a stream that unfolds into itself with arbitrary data at the beginning and end (so that it can be used as a real zip or gzip file, with a header and other necessary data).
Let's agree to use
Ln and Rn as abbreviations for literal(n) and repeat(n, n) , and the program assumes that each code is one byte. L0, respectively, is an analogue of NOP in Lempel-Ziv, L5 hello will output hello ; the same will output L3 hel R1 L1 o .A simple quine will look like this:
| Code | Conclusion | |||
|---|---|---|---|---|
| no-op | L0 | |||
| no-op | L0 | |||
| no-op | L0 | |||
| print 4 bytes | L4 L0 L0 L0 L4 | L0 L0 L0 L4 | ||
| repeat 4 last bytes | R4 | L0 L0 L0 L4 | ||
| print 4 bytes | L4 R4 L4 R4 L4 | R4 L4 R4 L4 | ||
| repeat 4 last bytes | R4 | R4 L4 R4 L4 | ||
| print 4 bytes | L4 L0 L0 L0 L0 | L0 L0 L0 L0 |
(It can be seen that the contents of the “Code” and “Output” columns are the same)
The interesting part of the program is a sequence of 6 bytes
L4 R4 L4 R4 L4 R4 , which outputs 8 bytes: R4 L4 R4 L4 R4 L4 R4 . That is, it outputs itself with one byte before and one after.If we write quine on Python, usually the problem is that the
print statement is always longer than what it prints. We solve this problem with recursion, substituting a line for printing into itself. Here we can use a different approach. The program on Lempel-Ziv is partially repeated, so that the repeated substring contains the entire original fragment. The recursion is here in the very presentation of the program, and not in execution. In any case, this fragment is crucial. Before the final R4, the output of the program is behind the input. After execution, output by one byte is ahead of input.L0 dummy operators can also be used in a more general version of the program, which can complement itself with an arbitrary three-byte prefix and suffix:| Code | Conclusion | |||
|---|---|---|---|---|
| print 4 bytes | L4 aa bb cc L4 | aa bb cc L4 | ||
| repeat 4 last bytes | R4 | aa bb cc L4 | ||
| print 4 bytes | L4 R4 L4 R4 L4 | R4 L4 R4 L4 | ||
| repeat 4 last bytes | R4 | R4 L4 R4 L4 | ||
| print 4 bytes | L4 R4 xx yy zz | R4 xx yy zz | ||
| repeat 4 last bytes | R4 | R4 xx yy zz |
(The output is the code plus
aa bb cc added to the beginning and xx yy zz added to the end)I had to spend most of Sunday to get to this point, but when I did it, I already knew that I had won. From my experiments, I found out that it is quite easy to create a program that outputs itself without several instructions, or even one that displays itself with a prefix, minus several instructions. The extra bytes
aa bb cc in the output allow you to add the necessary fragment to the program. It's also easy to write code that outputs itself, plus an extra three bytes xx yy zz . These two techniques can be used to add a header and additional data to the archive at the end.This is how a program with arbitrary prefix and suffix looks like:
| Code | Conclusion | |||
|---|---|---|---|---|
| print the prefix | [P] | P | ||
| output p +1 bytes | L p +1 [P] L p +1 | [P] L p +1 | ||
| repeat last p +1 bytes | R p +1 | [P] L p +1 | ||
| output 1 byte | L1 R p +1 | R p +1 | ||
| output 1 byte | L1 L1 | L1 | ||
| output 4 bytes | L4 R p +1 L1 L1 L4 | R p +1 L1 L1 L4 | ||
| repeat 4 last bytes | R4 | R p +1 L1 L1 L4 | ||
| output 4 bytes | L4 R4 L4 R4 L4 | R4 L4 R4 L4 | ||
| repeat 4 last bytes | R4 | R4 L4 R4 L4 | ||
| output 4 bytes | L4 R4 L0 L0 L s +1 | R4 L0 L0 L s +1 | ||
| repeat 4 last bytes | R4 | R4 L0 L0 L s +1 | ||
| no-op | L0 | |||
| no-op | L0 | |||
| output s +1 bytes | L s +1 R s +1 [S] | R s +1 [S] | ||
| repeat last s +1 bytes | R s +1 | R s +1 [S] | ||
| print suffix | [S] | S |
(The output is P, then the bytes from the “Code” column, then S.)
Unzip zip file
Now go to the real action. We solved the main technological problem of creating a recursive zip file, but there are still a few details left.
The first problem: to translate our quine, recorded in the simplified opcodes, into real Lempel-Ziv opcodes. RFC 1951 defines the DEFLATE format used in gzip and zip; a sequence of blocks, each of which contains a sequence of opcodes encoded by Huffman coding. Huffman coding assigns strings of different lengths to different opcodes, which does not coincide with our assumption that opcodes have the same length. But wait! We can, if we try, find a fixed length coding that can be used.
There are literal blocks and opcode blocks in DEFLATE. The header of the literal block is 5 bytes:

If our opcodes L occupy 5 bytes each, opcodes R must also occupy 5 bytes, and each byte above will be repeated five times (for example, the argument for L4 now takes 20 bytes and R4 repeats the last 20 bytes of output). The block of opcodes with one
repeat(20,20) takes a little less than 5 bytes:
Fortunately, the opcode block containing two instructions
repeat(20,10) does the same and takes exactly 5 bytes:
Coding a
repeat with a different argument length requires a few more complex tricks, but it seems that we can develop 5-byte codes that repeat a string between 9 and 64 bytes in length. For example, here are blocks repeating 10 and 40 bytes:

A block that repeats the last 10 bytes is 2 bits less than needed, but each block of repetition is followed by a block of literals that starts with three zero bits and is added to the border of the nearest byte. If the repeat block ends 2 bits before the boundary and a literal block follows, the fill-in will insert the missing two bits. In the same way, a block repeating 40 bytes goes out over the border by 5 bits, but these bits are zero. Starting block 5 bits later, we subtract these bits from the dobivka. Both of these tricks work because the last 7 bits of any repeat block are zero, and the bits in the first byte of the block of literals are also zero, so the border is not visible. If the literal block began with one bit, this cunning device would not have worked.
The second obstacle is that the zip archives (and gzip too) store the checksum of uncompressed data. Since uncompressed data is the same zip archive, the checksum is also involved in the calculation. So, we need to find such a value of
x , at which the checksum becomes equal to x . Recursion strikes back.The CRC32 command interprets the entire file as one large number and calculates the remainder when this number is divided by a specific constant using a special division method. We could write the corresponding equations and solve them for
x , but I’ll have enough recursive riddles for today. For x there are only a little more than 4 billion acceptable values, and we can easily find the necessary brute force.If you want to repeat all this on your own, a couple of simple problems await you, for example, make the length of the tar file share without a balance by 512 and compress the zip header to 59 bytes so that
Rs+1 no more than R64 . But this is just a programming issue.So, I got the files r.gz (gzip-archive), r.tar.gz (tar-file, compressed gzip), and r.zip (zip-archive). It is a pity, but I could not find a program that would recursively unpack these files to infinity. It would be fun to watch, but it looks like much less complicated zip-bombs have already spoiled us all the fun.
If you feel fit, here is rgzip.go , a Go program that generates these files. I wonder if you can create a zip file containing a gzip file containing the original zip file in turn). Ken Thompson suggested trying to create a zip-archive, unpacking his copy but slightly larger in size, so that when recursively unzipping the archive size grew indefinitely (if you succeed in one or the other, please leave a comment).
Source: https://habr.com/ru/post/119676/
All Articles