Geekly Articles each Day
📜 ⬆️ ⬇️

Fast calculation of accurate 3D distance map using CUDA technology

Distance Map is an object that allows you to quickly get the distance from a given point to a certain surface. Usually it is a matrix of distance values ​​for nodes with a fixed step. It is often used in games to determine “hitting” a player or object, and for optimization problems of combining objects: arrange objects as close as possible to each other, but so that they do not overlap. In the first case, the quality of the distance map (that is, the accuracy of the values ​​in the nodes) does not play a big role. In the second, life may depend on it (in a number of applications related to neurosurgery). In this article I will tell you how you can quite accurately calculate the map of distances in a reasonable time.

Main objects

Suppose we have some surface S given by a set of voxels. The coordinates of the voxels will be calculated on a regular grid (i.e., the steps for X, Y, and Z are the same).

It is required to calculate the distance map M [X, Y, Z] for all voxels that lie in a cube containing a surface; M [x, y, z] = d ((x, y, z), S) = min (d ((x, y, z), (S n x, S n y, S n z)) = sqrt (min ((xS n x) 2 + (yS n y) 2 + (zS n z) 2 )). The last equality is true only for a regular grid, the rest should be obvious.

Where does the data come from


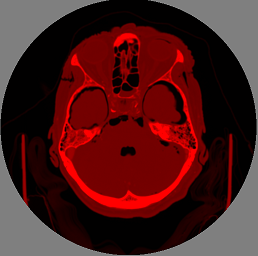
For our task, the data comes from the MRI . Let me remind you that we work with 3D images, so that the entire 3D image is a set of flat pictures for different slices in Z, which I, of course, cannot imagine everything here; they are slightly smaller than the X and Y resolution. The typical tomography size is about 625x625x592 voxels.
')

As a result of quite tricky transformations, the boundary of the surface of the head is highlighted. The very essence of these transformations is reduced to a variety of filters that remove the "noise" and the function that defines the actual boundary by gradient. There is nothing new here, about such things was told in the subject “Image Processing”, in particular . Actually, the boundary is the target set, to which we will calculate distances and build a map.

Brute force

Let us estimate to begin with, why not fill the distance map with the values ​​“by definition” - the minimums of the distances to the points of the border. Total points of the map: X * Y * Z, surface points of order max (X, Y, Z) 2 . Recall the size of the source data and get something about 592 * 625 4 arithmetic logic operations. The calculator will tell you that this is more than 90,000 billion. To put it mildly, a bit too much, let's postpone until a direct search.

Dynamic programming

This suggests the use of data presented in a three-dimensional array; you can somehow calculate the value at each point using its neighbors, and of course we are not the first to do this. Somewhat repels the fact that keeping in memory a structure of size 592 * 625 * 625 * sizeof (float), which is about 1 Gigabyte, is somewhat resource-intensive. Well, okay, let's forget for now that tomography can be removed with a double resolution (8 more times more) - 640Kbyte has long been missing.

The most trivial method of filling (city-block), similar to the algorithm for traversing the maze , works out in a matter of seconds, but the maximum error on the three-dimensional grid can be 42 grid steps for the maximum calculated distance of 50 steps. How bad is it? Complete failure.

A single algorithm from the class ( central point ) gives almost satisfactory accuracy (an error of no more than 0.7 grid steps), but minutes are running.

We tried to find a compromise by implementing the chessboard distance (described in the same article as the central point), but the final accuracy could not be arranged, and the time of its work was tens of seconds.

A picture is a link to a full-sized one, but even on the preview you can see “strange” behavior far enough from the surface points, and especially if you need to cheat more internal objects. On the left is the chessboard, and on the right is what was obtained by brute force. And once again I remind you that for those who look only at the pictures - we are talking about 3D images, so strange “punctures” inside are explainable - they are caused by proximity to the surface on the next or previous slides in Z. In general, failure.

Brute force again

Yes, the word CUDA in the picture as if hints. Maybe 90000 billion - not so much, but maybe this number can be somehow reduced, without loss of accuracy. In any case, the middle-end video card copes with primitive computational operations 80-120 times faster than a processor of a similar class. Let's try.

Yes, brute force has a significant advantage - there is no need to keep the entire distance map in memory, and as a result - linear scalability.

Brute force reduction

Thesis: it makes no sense for each point to check the distance to each point of the border. In fact, the distance map is obliged to ensure good accuracy only in the immediate vicinity of the border, rather distant points can not be considered at all, and the intermediate ones can be marked with an approximate distance.

The criterion of correctness is absolute accuracy near the border (at a distance of 10 (GUARANTEED_DIST) grid steps), good accuracy at a distance of 36 (TARGET_MAX_DIST) steps, and visual adequacy (without artifacts - why confuse surgeons). The numbers 10 and 36 came directly from our problem (we generally have the values ​​in millimeters and the millimeter grid).

Cubic index

For each point I would like to determine how accurately its value should be calculated. It is obvious that the size of such a structure will coincide with the size of the original image, and this is a lot and will be considered for a long time.

We will merge points into “cubes”. Let the die size be 32 (CUBE_SIZE), then the index will have dimensions of 20 x 20 x 19.

Mark the cube as the "best" point lying in it. If at least one point requires an exact calculation, we count the whole cube for sure. In the worst case, we do not count at all.

How to quickly mark the cubes? Let's start with the points of the border: add to each of them an offset of GUARANTEED_DIST in all 27 directions ((-1,0,1) x (-1,0,1) x (-1,0,1)), we get the index of the corresponding die, by dividing by 32 (CUBE_SIZE), and mark it as “exact” - because it contains at least one point that requires accurate calculation. Task: explain why this is enough, and all cubes containing points for accurate calculation will be marked correctly.

Just in case, the rather trivial code that it executes is:

for (size_t t = 0; t < borderLength; t++)
{
for ( int dz = -1; dz <= 1; dz++)
for ( int dy = -1; dy <= 1; dy++)
for ( int dx = -1; dx <= 1; dx++)
{
float x = border[t].X + ( float )dx * GUARANTEED_DIST;
float y = border[t].Y + ( float )dy * GUARANTEED_DIST;
float z = border[t].Z + ( float )dz * GUARANTEED_DIST;
if (x >= 0 && y >= 0 && z >= 0)
{
size_t px = round(x / CUBE_SIZE);
size_t py = round(y / CUBE_SIZE);
size_t pz = round(z / CUBE_SIZE);
size_t idx = px + dim_X * (py + skip_Y * pz);
if (idx < dim_X * dim_Y * dim_Z)
{
markedIdx[idx] = true ;
}
}
}
}


On practical data, this idea allowed to reduce the order of “all” enumeration by 4-5 times. Anyway, it turns out a lot, but the idea with the cubes will still come in handy.

Cubic container

In fact, it makes no sense to calculate the distance to all points of the boundary; it suffices to calculate it only for the nearest points; and now we know how to organize such a structure.

Scatter all voxels of the S boundary into cubes (we will forget about index cubes from the present moment; we have built them, understood how to use them, and now we don’t work with them anymore). In each cube we will put those points of the boundary that are reachable (lie at a distance of TARGET_MAX_DIST and less). To do this, it is enough to calculate the center of the cube, and postpone the distance sqrt (3) / 2 * CUBE_SIZE (this is the diagonal of the cube) + TARGET_MAX_DIST. If a point is reachable from the top of the cube or from any point on the side, then it is reachable from its inside.

I think it makes no sense to give the code, it is very similar to the previous one. And the correctness of the idea is also obvious, but one essential point remains: in fact, we “multiply” points of the border, the number of which can increase up to 27 times with a reasonable TARGET_MAX_DIST (smaller cube size) and even more times different.

Optimization:

I deliberately will not give exact algorithms for both points (what if you implement them better and become our competitors?;)), There are more words than ideas.

In general, the cubes reduce the brute force order by X / CUBE_SIZE * Y / CUBE_SIZE * Z / CUBE_SIZE times, but we must remember that reducing the size of the die will require significantly more memory, and the threshold value for our images turned out to be around 24-32.

Thus, the task has been reduced to about 100-200 billion material operations. Theoretically, it is computable on a video card in tens of seconds.

CUDA Core

It turned out so simple and beautiful that I will not be too lazy to show it:

__global__ void minimumDistanceCUDA( /*out*/ float *result,
/*in*/ float *work_points,
/*in*/ int *work_indexes,
/*in*/ float *new_border)
{
__shared__ float sMins[MAX_THREADS]; // max threads count

for ( int i = blockIdx.x; i < BLOCK_SIZE_DIST; i += gridDim.x)
{
sMins[threadIdx.x] = TARGET_MAX_DIST*TARGET_MAX_DIST;

int startIdx = work_indexes[2*i];
int endIdx = work_indexes[2*i+1];

float x = work_points[3*i];
float y = work_points[3*i+1];
float z = work_points[3*i+2];

// main computational entry
for ( int j = startIdx + threadIdx.x; j < endIdx; j += blockDim.x)
{
float dist = (x - new_border[3*j] )*(x - new_border[3*j] )
+ (y - new_border[3*j+1])*(y - new_border[3*j+1])
+ (z - new_border[3*j+2])*(z - new_border[3*j+2]);
if (dist < sMins[threadIdx.x])
sMins[threadIdx.x] = dist;
}

__syncthreads();

if (threadIdx.x == 0)
{
float min = sMins[0];
for ( int j = 1; j < blockDim.x; j++)
{
if (sMins[j] < min)
min = sMins[j];
}
result[i] = sqrt(min);
}

__syncthreads();
}
}


We load the block of coordinates of the distance map points for enumeration (work_points), the corresponding starting and ending indices for enumerating the boundary points (work_indexes) and the border optimized by the algorithm with “cubes” (new_border). The results are taken in single real accuracy.

Actually, the kernel code itself, which is pleasantly very understandable, even without the subtleties of CUDA. Its main feature is the use of variables gridDim.x and threadIdx.x denoting the indices of the current thread from the set of running threads on the video card - they all do the same thing, but with different points, and then the results are synchronized and accurately recorded.

It remains only to correctly organize the calculation of work_points on the CPU (but it's so easy!) And start the calculator:
#define GRID 512 // calculation grid size
#define THREADS 96 // <= MAX_THREADS, optimal for this task
minimumDistanceCUDA<<<GRID, THREADS>>>(dist_result_cuda, work_points_cuda, work_indexes_cuda, new_border_cuda);

On the Core Duo E8400 and the GTX460 video card, the average tomography is processed within a minute , the memory consumption is limited to 512 MB. The allocation of CPU time is about 20 percent on the CPU and file operations, and the remaining 80 on the calculation of the minima on the video card.

And here is what the picture looks like with the “deafening” of distant points:



Somehow, I hope something useful to you. A big request, do not copy the pictures and do not re-publish without my permission (I am the author of the method, although it is difficult to call it “method”).

Have a good day!

Source: https://habr.com/ru/post/119603/

More articles:


All Articles