Russian Code Cup: the most interesting of the tasks of the first stage
On May 8, the first qualifying round of the Russian Code Cup All-Russian Programming Cup took place . The winner of the round was Eugene Kapun, who solved all 5 problems with a penalty time of 130 minutes.
In total, 756 people took part in the first qualifying round. According to the results of the round, the top 200 participants were allowed to participate in the qualifying round, which will be held on June 19th.
The 2nd and 3rd qualifying rounds will be held on May 14 and 15, at which another 400 people will be selected.
')
In this article, we will analyze the various statistics of the first stage of the RCC, analyze the problems and answer the most frequently asked questions that were received during the tour.
The jury was offered 5 tasks to solve. At least one task was solved by 691 participants. The simplest task was A, it was solved by 685 participants. In general, the right solutions were distributed to the tasks as follows:

Diagram 1. The number of correct solutions for the tasks.
As can be seen from the diagram, tasks A, B and C submitted to the majority of participants, but D and E turned out to be much more difficult. These tasks became the key to successful qualification - the solution of three simple tasks and at least one of the two difficult guaranteed the passage to the qualifying round - only 87 participants coped with four or more tasks.
But participants with three solved tasks needed to demonstrate a high speed of solving problems. The “cut-off” of the two-hundredth place went through the penalty time: to enter the qualifying round with three tasks, it was necessary to have a penalty time of no more than 141, that is, an average of 23.5 minutes was spent on the task.
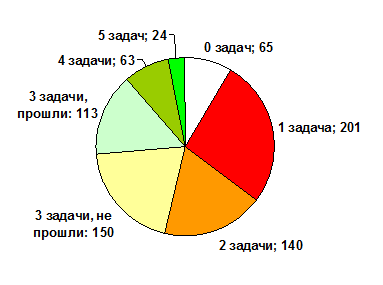
Diagram 2. Number of participants depending on the number of solved problems.
The largest number of attempts was made on task B: 1952, with only 461 of them, that is, about 24% were successful. In general, the percentage of successful attempts on tasks is as follows:

Chart 3. The percentage of successful attempts on tasks.
It can be seen that although problem C was solved by fewer participants, it gave them fewer problems than B. Similarly, the more difficult task E contained less “pitfalls” than task D.
It is interesting to see the statistics on programming languages that were used by the participants of the Russian Code Cup. If you transfer the total quantity to a pie chart, you get the following picture:
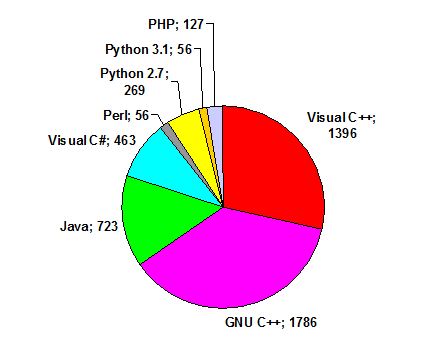
Diagram 4. The number of solutions depending on the programming language.
With a fairly large margin, GNU C leads the way, Java and C # totally occupy about three times less, in other languages even fewer approaches have been made.
Interestingly, the fifth problem, which required long arithmetic, was mainly solved in Java:
In general, the distribution of decisions sent by minute of the competition can be viewed in the following graph:
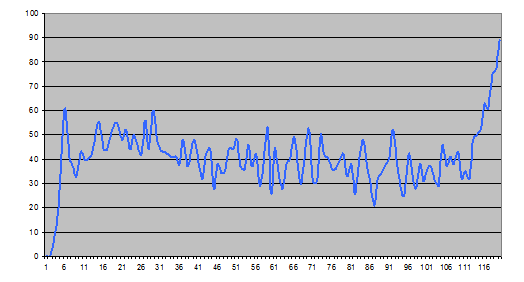
Chart 4. The number of approaches depending on the minute of the competition.
It can be seen that in the first minutes the participants read the tasks, then there was a sharp surge, when the majority of strong participants coped with the first task, a slight decline, and then the number of approaches ranged from 30 to 50 per minute, with a surge to almost 90 at the end of the round. At the same time, if at the beginning of the competition, the right decisions were mainly sent to check, then towards the end, the share of the right decisions steadily declined. The following graph shows the dependence of the proportion of correct decisions among those sent to the test, depending on the minute of the competition.

Chart 5. The share of successful approaches, depending on the minute of the competition.
Analysis of tasks
Problem A. String concatenation
In many applications, it is necessary to perform various operations with strings. Two fairly frequent operations are reversing a line and concatenating two or more lines.
As a result of the reversal of the string s, we get the string s R , which consists of the same characters as s, but going in reverse order. For example, the result of the reversal of the string “abcde” is the string “edcba”. Further in this problem, instead of the notation s R , the notation (s) will be used.
As a result of the concatenation of two strings s and t, we get the string s t , in which the characters of the string s are written first, and then the characters of the string t. The concatenation of three, four and more lines is defined in a similar way. For example, concatenating the strings “abc” and “cda” results in the string “abccda”
Your task is to determine the result of concatenation of several strings, some of which need to be expanded.
Input Format
Input data consists of a single line that contains only lowercase Latin letters and parentheses. Its length does not exceed 200 characters. This line describes the concatenation of several lines, some of which need to be expanded.
In the given line, there is a closing one to the right of each opening bracket, there is an opening one to the left of each closing one, and there are no other brackets between the opening and closing brackets corresponding to each other and there is at least one letter.
Output format
Output the result of the concatenation.
Decision
This was the easiest task in the competition. The restrictions are very small and you can solve the problem in any reasonable way. For example, read a string, break it into fragments, use round brackets as delimiters, and expand all even-numbered blocks. In languages in the built-in processing of regular expressions (for example, Perl) the solution to this problem in general looks particularly compact and natural.
We will give a solution to this problem in all programming languages available on the Russian Code Cup. At the same time we will pay attention to how to read data from the standard input stream - many participants asked during the competition about where to get the input data.
We do not pretend to optimal solutions, and on the contrary, we tried to bring slightly different solutions in different languages.
Java:
C ++:
C #:
Perl:
Python
Php
Please note that the solution to this problem turned out to be particularly simple and compact in Perl and PHP.
Problem B. Tariffs
Currently, almost every mobile operator has an extensive set of tariffs that allow each person to choose the most suitable for themselves. Unfortunately, it is often very difficult to manually make this choice.
At one of the cellular operators, each tariff is characterized by three numbers: subscriber fee ci (set in rubles), minimum chargeable time unit t i (set in seconds), cost of minimum chargeable time unit pi (set in kopecks, 100 rubles in one ruble). The total cost of calls per month consists of the subscription fee and the cost of each of the outgoing calls. The cost of a call when using the i-th tariff is calculated as follows: let the talk time be T seconds. If T <t i , then the cost of the call is zero. Otherwise, the call cost is equal to the product of k by p i , where k is the minimum integer such that k • t i ≥ T.
The description of tariffs and statistics of outgoing calls of the subscriber during the month are given - their number m and duration d 1 , ..., d m in seconds. It is necessary to find a tariff at which the total cost of these calls would be minimal.
Input Format
The first line contains two integers n and m - respectively, the number of tariffs and outgoing calls of the subscriber (1 ≤ n, m ≤ 100). Each of the next n lines describes one tariff and contains three integers: c i (0 ≤ c i ≤ 100), t i (1 ≤ t i ≤ 3600), p i (0 ≤ p i ≤ 1000).
The last line contains m integers d 1 , ..., d m (1 ≤ di ≤ 3600 for all i from 1 to m).
Output format
Output one number - the tariff number, using which the total cost of the subscriber’s outgoing calls for the month in question is minimal. Tariffs are numbered with integers from 1 to n in the order in which they are specified in the input file. If there are several such tariffs, print the number of any of them.
Decision
This task checked participants for attentiveness while reading the conditions. There are two main “thin points” in this task: the subscription fee is set in rubles, and the cost of a call in kopecks, as well as the features of rounding off the talk time: the conversation is less than one payable unit is rounded to zero, and the call above one chargeable unit is rounded up.
If you notice these two points, the solution is to directly implement the calculation of the cost of calls at each of the specified tariffs and select the optimal one.
Problem C. K-sort
The task of sorting is to order a given array of numbers (or other objects) in ascending or descending order. This task has enough many options, for many of which there are very efficient algorithms. One of the important parameters of these algorithms is the number of exchanges of the array elements necessary for ordering.
Next we will consider the sorting option, which we will call k-sorting. In this variant it is allowed to swap the values of two array elements with numbers that differ by exactly k in one operation (called k-exchange). For example, if the initial array has the form [6, 10, 4, 1, 2], and k = 3, then this array can be ordered in ascending order in two operations (after the first exchange, the array will look like [1, 10, 4, 6 , 2], and after the second - [1, 2, 4, 6, 10]).
An array of integers a 1 , ..., a n is given . Your task is to determine the minimum number of k-exchanges needed to order this array in descending order.
Input Format
The first line contains an integer n (1 ≤ n ≤ 300). The second line contains n integers a1, ..., an (1 ≤ ai ≤ 109 for all i from 1 to n). The third line contains an integer k (1 ≤ k ≤ n - 1).
Output format
If the given array can be ordered in non-decreasing order using operations of the type described, then output the minimum number of k-exchanges necessary for sorting. Otherwise, print one number -1.
Decision
We divide the array into k parts, depending on the rest of the position modulo k. In each of these parts, the neighboring elements are at a distance k, so they can be exchanged between them. Elements from different parts of the array cannot be exchanged among themselves.
Note that in a sorted array, each of the parts will also be sorted. Consequently, our task was reduced to the following: sort each of the parts for the minimum number of actions and verify that the resulting array was sorted. If so, then the answer is the total number of actions required to sort the parts. If the array is unordered, then there is no solution.
It remains to understand what is the minimum number of actions necessary to sort an array if it is allowed to exchange only neighboring elements (namely, by such operations we must sort each of the parts). It turns out that the minimum number of actions is performed by regular bubble sorting. Let n be the length of the array a [0..n - 1] that you want to sort. Then the required number of exchanges performs the following algorithm:
Let us prove it: for this we consider the following characteristic of the array, which is called the number of inversions: the number of pairs of positions (i, j) , where i < j and a [i]> a [j] . It is clear that in the sorted array the number of inversions is zero. On the other hand, the exchange of two neighboring elements can change the number of such pairs by no more than one. In this case, the sorting of the bubble during each exchange reduces the number of inversions by one.
Therefore, the number of exchanges in bubble sorting is equal to the number of inversions in the array, that is, the minimum number of exchanges that must be performed to sort the array.
Task D. Rails
An important parameter of the railway is the gauge - the distance between the two rails on which the train travels. It is this parameter that determines the types of trains and other cars that can travel by rail.
Recently, a space expedition to the planet RCC-0805 found out that there are railways on this planet too. It was even found the railway depot, but to determine the width of the track so far failed. The fact is that the railways on this planet fit without sleepers, therefore, it is not always easy to determine which rails correspond to each other.
The plan for the location of the rails in the railway depot is set. For simplicity, we assume that the territory is an infinite plane, and each rail is represented as a straight line. It is necessary to find the minimum width of the track d, at which the rails can be divided into pairs so that in each pair they are parallel and the distance between them is d.
Input Format
The first line contains an integer n (1 ≤ n ≤ 2000). Each of the next 2n lines contains four integers x i, 1, y i, 1, x i, 2, y i, 2 - the coordinates of two different points through which the rail passes. All coordinates do not exceed 1000 in absolute value. The straight lines corresponding to different rails do not coincide.
Output format
Print a real number - the minimum possible track width. It must be determined with an accuracy of no worse than 10 -6 .
If it is impossible to divide the rails into pairs with the requirements of the task at any track width, output the number −1.
Decision.
First, we divide the rails into equivalence classes in the direction of a straight line - parallel straight lines will fall into one class. After that, in each class we find all possible acceptable values of the gauge width for this class. The answer is the minimum possible distance that is suitable for all classes.
Now let's take a closer look at each of the stages of the solution.
To distribute straight lines by equivalence classes, we construct an equation for each of the straight lines. Let a straight line pass through points (x 1 , y 1 ), (x 2 , y 2 ). Then its equation of the form ax + by + c = 0 can be found as follows: a = y 1 - y 2 , b = x 2 - x 1 , c = - (ax 1 + by 1 ). It is now useful to normalize the coefficients of a straight line, dividing a, b and c by . Now, each line has two representations: up to multiplication of coefficients by –1. In order for each straight line to have a unique equation, it is convenient to additionally require the conditions “a> 0 or (a = 0 and b> 0)”. When this requirement is fulfilled, parallel lines have the same pair (a, b). In this representation, it is also convenient to calculate the distance between the straight lines: for two parallel straight lines ax + by + c 1 = 0 and ax + by + c 2 = 0, the distance is | c 1 - c 2 |.
. Now, each line has two representations: up to multiplication of coefficients by –1. In order for each straight line to have a unique equation, it is convenient to additionally require the conditions “a> 0 or (a = 0 and b> 0)”. When this requirement is fulfilled, parallel lines have the same pair (a, b). In this representation, it is also convenient to calculate the distance between the straight lines: for two parallel straight lines ax + by + c 1 = 0 and ax + by + c 2 = 0, the distance is | c 1 - c 2 |.
Consider the class of parallel lines. We sort them by coefficient c. Consider the first straight line - it is paired with one of the other straight lines of this class. Let's go through this line. Let the distance between them be d. Now we greedily build a partition of straight lines into pairs at a distance d. If this can be done, then d can be the gauge for this class. We will consider straight lines in ascending order c. If the next straight line c = c i and has no pair yet, then it should be parallel to it at distance d with c = c i + d. If there is such a line, we pair it with the line in question. The pairing can be implemented in linear time using the two-pointer method: it suffices to note that c + d also increases with increasing c.
Finally, consider looking for an answer: let there be lists of possible answers for each of the classes. Naturally, they are sorted in ascending order. Two such lists can be easily crossed in one pass. After completing the intersection of all the lists, in a time proportional to the sum of their lengths, we obtain an intersection list, the minimum element of which is the answer to the problem.
Let's analyze the running time of the algorithm. Class distribution is done in O (n). For a given class of size k, the construction of a list of admissible distances is performed in O (k 2 ) and its length does not exceed k. Therefore, the last step is performed in O (n), and the entire algorithm in O (n 2 ).
Problem E. Guess the number
Recently, in one popular social network appeared the application "Guess the number!". Its users are offered a game, at each of the levels of which it is necessary to determine the hidden number from some information about it.
In particular, at one of the most difficult levels, it is necessary to guess a rational number x (0 <x <1), which is known that as a result of multiplying by a natural number k, exactly one change occurred in its decimal notation - the i-th one changed places in it and the j-th digit after the decimal point (the digits are numbered from one in the direction from left to right). At the same time, the digit to the decimal point has not changed, that is, the inequality 0 <k x <1 is fulfilled. Note that there can be infinitely many digits after the decimal point in the decimal notation x.
Your task is to write a program that will determine the value of x by the numbers i, j, k.
Input Format
The first line contains three integers i, j, k (1 ≤ i <j ≤ 1000; 2 ≤ k ≤ 109).
Output format
If the desired number exists, then print two integers - the numerator a and the denominator b of an irreducible fraction specifying the desired number (a, b> 0). Otherwise, print the phrase NO SOLUTION.
Decision
Suppose that initially at the i-th position is the digit s, and at the j-th position - the digit t. Then, after multiplying by k, the number is equal to x - 10 –i s + 10 –i t – 10 –i t + 10 –i s. Therefore, the required number is a solution to the equation kx = x - 10 –i s + 10 –i t - 10 –i t + 10 –i s.
Note that in fact the solution does not depend on the specific values of s and t, but only on their difference: (k - 1) x = (10 –i - 10 –i ) (t - s). In addition, s <t. Therefore, it is enough to go through the difference (t - s) in the range from 1 to 9. For each value of the difference, we find the solution to the equation and check it: make sure that when the number is multiplied by k, the numbers on the i-th and j-th positions in the decimal record change in some places, and the integer part remains zero.
Validation is necessary because, due to transferences, the solution of the reduced equation may not correspond to the solution of the problem.
Answers to frequently asked questions
During the competition, participants could send questions to the jury. Some questions were met especially often, and we decided to answer them in this article.
Question: Should I send the source code or the compiled file for review?
Answer: send the source code for review. The checking system itself compiles the decision of the participant, the command lines are specified in the rules of the Russian Code Cup
Question: where should I enter the data?
Answer: data should be entered from the so-called standard input stream. This corresponds to keyboard input, if you run a program that reads data from the standard input stream without additional parameters, the input will be from the keyboard.
In this case, low-level keyboard input, like analyzing keystrokes or receiving operating system messages about keystrokes, is the wrong approach. Read should be "from the console."
Question: where should I enter the answer?
The answer must be output to the standard output stream (by default, it is sent to the screen). Again, do not try to do this with low-level tools.
Let us give examples of reading the standard input stream and writing to the standard output stream in all programming languages that are supported in the Russian Code Cup.
Java
For input, use the System.in stream. The most convenient tools for parsing Java input are the BufferedReader and Scanner classes. BufferedReader is faster in reading and allows you to quickly read a large amount of data in rows. The scanner is slower due to the use of regular expressions, but it makes it very flexible to parse the input string, for example, read one number from the input.
To read from the standard input stream using BufferedReader, you should write a line in the program:
BufferedReader in = new BufferedReader (new InputStreamReader (System.in));
To read from the standard input stream using Scanner, write the following line in the program:
Scanner in = new Scanner (System.in);
For output, use System.out. In this case, System.out is non-caching (immediately flushes its buffer), if you need to output a large amount of information, it is better to wrap it in a PrintWriter.
C ++
You can use scanf for typing in the classic C style. This function reads data just from the standard input stream.
Input through streams is done using the cin stream. By default, it is set to standard input. Note that input using streams is significantly slower than input using scanf, so the program may not be able to read large amounts of data.
Again, you can use classic printf or stream cout for output. All performance notes remain valid for them - printf is faster.
C #
Use the Console for input. Console.ReadLine () reads the next line of input. To parse it, use the split () method. Converting data into numbers is done by the class Convert.
Console should also be used for output. For example, to display the number x, you can write Console.WriteLine (x).
Python
You can use input or raw_input functions for input. You can also use the sys.stdin file descriptor, which is configured on the standard input stream.
For output, we recommend using print.
Perl
Input from standard input in Perl is done with the <> command. This command reads a string from a file and returns it.
For output, we recommend using print.
Php
Input from standard input in PHP is done from the STDIN descriptor. The next line can be considered, for example, the fgets command.
You can use print or echo for output.
When using various functions of reading a string, we also recommend that you carefully read the documentation and pay attention to whether the function returns a newline along with the string. In the jury's tests, all lines, including the last, end with a line break, testing is conducted under Windows 7, the combination adopted in Windows is used to translate a line consisting of characters with codes 13 and 10.
In addition, you should note that testing is done automatically. Therefore, you should not try to display various “invitations to input” or try to “decorate” the output. You must enter the data, solve the problem and output the data, clearly following the output format.
Question: Is the test correct in the example?
Answer: the test in the example is usually correct - it is checked by several people, including several people who solve problems without knowing them in advance. If it seems to you that the test example is incorrect, then read more carefully the condition, probably you understand something wrong.
If it still seems to you that the example is incorrect, include in the request a detailed description of why you consider the example incorrect, which answer is correct, what do you think is inaccurate or ambiguous.
Question: Is the 239th test correct in problem X?
Answer: most likely the test is correct. If you think the test is wrong, write why you think so. Just the question "is this a test right" is pointless to ask. - «» - , .
: , ?
: , .
!
Russian Code Cup
In total, 756 people took part in the first qualifying round. According to the results of the round, the top 200 participants were allowed to participate in the qualifying round, which will be held on June 19th.
The 2nd and 3rd qualifying rounds will be held on May 14 and 15, at which another 400 people will be selected.
')
In this article, we will analyze the various statistics of the first stage of the RCC, analyze the problems and answer the most frequently asked questions that were received during the tour.
The jury was offered 5 tasks to solve. At least one task was solved by 691 participants. The simplest task was A, it was solved by 685 participants. In general, the right solutions were distributed to the tasks as follows:

Diagram 1. The number of correct solutions for the tasks.
As can be seen from the diagram, tasks A, B and C submitted to the majority of participants, but D and E turned out to be much more difficult. These tasks became the key to successful qualification - the solution of three simple tasks and at least one of the two difficult guaranteed the passage to the qualifying round - only 87 participants coped with four or more tasks.
But participants with three solved tasks needed to demonstrate a high speed of solving problems. The “cut-off” of the two-hundredth place went through the penalty time: to enter the qualifying round with three tasks, it was necessary to have a penalty time of no more than 141, that is, an average of 23.5 minutes was spent on the task.

Diagram 2. Number of participants depending on the number of solved problems.
The largest number of attempts was made on task B: 1952, with only 461 of them, that is, about 24% were successful. In general, the percentage of successful attempts on tasks is as follows:

Chart 3. The percentage of successful attempts on tasks.
It can be seen that although problem C was solved by fewer participants, it gave them fewer problems than B. Similarly, the more difficult task E contained less “pitfalls” than task D.
It is interesting to see the statistics on programming languages that were used by the participants of the Russian Code Cup. If you transfer the total quantity to a pie chart, you get the following picture:

Diagram 4. The number of solutions depending on the programming language.
With a fairly large margin, GNU C leads the way, Java and C # totally occupy about three times less, in other languages even fewer approaches have been made.
Interestingly, the fifth problem, which required long arithmetic, was mainly solved in Java:
In general, the distribution of decisions sent by minute of the competition can be viewed in the following graph:

Chart 4. The number of approaches depending on the minute of the competition.
It can be seen that in the first minutes the participants read the tasks, then there was a sharp surge, when the majority of strong participants coped with the first task, a slight decline, and then the number of approaches ranged from 30 to 50 per minute, with a surge to almost 90 at the end of the round. At the same time, if at the beginning of the competition, the right decisions were mainly sent to check, then towards the end, the share of the right decisions steadily declined. The following graph shows the dependence of the proportion of correct decisions among those sent to the test, depending on the minute of the competition.

Chart 5. The share of successful approaches, depending on the minute of the competition.
Analysis of tasks
Problem A. String concatenation
In many applications, it is necessary to perform various operations with strings. Two fairly frequent operations are reversing a line and concatenating two or more lines.
As a result of the reversal of the string s, we get the string s R , which consists of the same characters as s, but going in reverse order. For example, the result of the reversal of the string “abcde” is the string “edcba”. Further in this problem, instead of the notation s R , the notation (s) will be used.
As a result of the concatenation of two strings s and t, we get the string s t , in which the characters of the string s are written first, and then the characters of the string t. The concatenation of three, four and more lines is defined in a similar way. For example, concatenating the strings “abc” and “cda” results in the string “abccda”
Your task is to determine the result of concatenation of several strings, some of which need to be expanded.
Input Format
Input data consists of a single line that contains only lowercase Latin letters and parentheses. Its length does not exceed 200 characters. This line describes the concatenation of several lines, some of which need to be expanded.
In the given line, there is a closing one to the right of each opening bracket, there is an opening one to the left of each closing one, and there are no other brackets between the opening and closing brackets corresponding to each other and there is at least one letter.
Output format
Output the result of the concatenation.
Decision
This was the easiest task in the competition. The restrictions are very small and you can solve the problem in any reasonable way. For example, read a string, break it into fragments, use round brackets as delimiters, and expand all even-numbered blocks. In languages in the built-in processing of regular expressions (for example, Perl) the solution to this problem in general looks particularly compact and natural.
We will give a solution to this problem in all programming languages available on the Russian Code Cup. At the same time we will pay attention to how to read data from the standard input stream - many participants asked during the competition about where to get the input data.
We do not pretend to optimal solutions, and on the contrary, we tried to bring slightly different solutions in different languages.
Java:
import java.io.*; public class concat_as { public static void main(String[] args) throws IOException { BufferedReader in = new BufferedReader( new InputStreamReader(System.in)); String[] s = in.readLine().split("[()]"); for (int i = 0; i < s.length; i++) { if (i % 2 == 0) { System.out.print(s[i]); } else { System.out.print(new StringBuilder(s[i]).reverse()); } } } } C ++:
#include <string> #include <iostream> #include <algorithm> using namespace std; int main () { string s; cin >> s; int l = 0; while (l < s.length()) { if (s[l] == '(') { int r = l; while (s[r] != ')') r++; string tmp = s.substr(l + 1, r - l - 1); reverse(tmp.begin(), tmp.end()); cout << tmp; l = r + 1; } else { cout << s[l]; l++; } } return 0; } C #:
using System; using System.Linq; class concat_as { static void Main(string[] args) { string s = Console.ReadLine(); int L, R; do { L = s.IndexOf("("); R = s.IndexOf(")"); if (L >= 0) { Console.Write(s.Substring(0, L)); Console.Write(new string( s.Substring(L + 1, R - L - 1).Reverse().ToArray())); s = s.Substring(R + 1); } } while (L >= 0); Console.WriteLine(s); } } Perl:
$s = <>; $s =~ s/\(([^)]*)\)/reverse($1)/eg; print $s Python
s = raw_input() ans = '' for t in s.split('('): if ')' in t: l = t.split(')') ans += l[0][::-1] + l[1] else: ans += t print ans Php
<?php $s = trim(fgets(STDIN)); $s = preg_replace('#\((\w+)\)#se', 'strrev("\1")', $s); echo "$s\n"; ?> Please note that the solution to this problem turned out to be particularly simple and compact in Perl and PHP.
Problem B. Tariffs
Currently, almost every mobile operator has an extensive set of tariffs that allow each person to choose the most suitable for themselves. Unfortunately, it is often very difficult to manually make this choice.
At one of the cellular operators, each tariff is characterized by three numbers: subscriber fee ci (set in rubles), minimum chargeable time unit t i (set in seconds), cost of minimum chargeable time unit pi (set in kopecks, 100 rubles in one ruble). The total cost of calls per month consists of the subscription fee and the cost of each of the outgoing calls. The cost of a call when using the i-th tariff is calculated as follows: let the talk time be T seconds. If T <t i , then the cost of the call is zero. Otherwise, the call cost is equal to the product of k by p i , where k is the minimum integer such that k • t i ≥ T.
The description of tariffs and statistics of outgoing calls of the subscriber during the month are given - their number m and duration d 1 , ..., d m in seconds. It is necessary to find a tariff at which the total cost of these calls would be minimal.
Input Format
The first line contains two integers n and m - respectively, the number of tariffs and outgoing calls of the subscriber (1 ≤ n, m ≤ 100). Each of the next n lines describes one tariff and contains three integers: c i (0 ≤ c i ≤ 100), t i (1 ≤ t i ≤ 3600), p i (0 ≤ p i ≤ 1000).
The last line contains m integers d 1 , ..., d m (1 ≤ di ≤ 3600 for all i from 1 to m).
Output format
Output one number - the tariff number, using which the total cost of the subscriber’s outgoing calls for the month in question is minimal. Tariffs are numbered with integers from 1 to n in the order in which they are specified in the input file. If there are several such tariffs, print the number of any of them.
Decision
This task checked participants for attentiveness while reading the conditions. There are two main “thin points” in this task: the subscription fee is set in rubles, and the cost of a call in kopecks, as well as the features of rounding off the talk time: the conversation is less than one payable unit is rounded to zero, and the call above one chargeable unit is rounded up.
If you notice these two points, the solution is to directly implement the calculation of the cost of calls at each of the specified tariffs and select the optimal one.
Problem C. K-sort
The task of sorting is to order a given array of numbers (or other objects) in ascending or descending order. This task has enough many options, for many of which there are very efficient algorithms. One of the important parameters of these algorithms is the number of exchanges of the array elements necessary for ordering.
Next we will consider the sorting option, which we will call k-sorting. In this variant it is allowed to swap the values of two array elements with numbers that differ by exactly k in one operation (called k-exchange). For example, if the initial array has the form [6, 10, 4, 1, 2], and k = 3, then this array can be ordered in ascending order in two operations (after the first exchange, the array will look like [1, 10, 4, 6 , 2], and after the second - [1, 2, 4, 6, 10]).
An array of integers a 1 , ..., a n is given . Your task is to determine the minimum number of k-exchanges needed to order this array in descending order.
Input Format
The first line contains an integer n (1 ≤ n ≤ 300). The second line contains n integers a1, ..., an (1 ≤ ai ≤ 109 for all i from 1 to n). The third line contains an integer k (1 ≤ k ≤ n - 1).
Output format
If the given array can be ordered in non-decreasing order using operations of the type described, then output the minimum number of k-exchanges necessary for sorting. Otherwise, print one number -1.
Decision
We divide the array into k parts, depending on the rest of the position modulo k. In each of these parts, the neighboring elements are at a distance k, so they can be exchanged between them. Elements from different parts of the array cannot be exchanged among themselves.
Note that in a sorted array, each of the parts will also be sorted. Consequently, our task was reduced to the following: sort each of the parts for the minimum number of actions and verify that the resulting array was sorted. If so, then the answer is the total number of actions required to sort the parts. If the array is unordered, then there is no solution.
It remains to understand what is the minimum number of actions necessary to sort an array if it is allowed to exchange only neighboring elements (namely, by such operations we must sort each of the parts). It turns out that the minimum number of actions is performed by regular bubble sorting. Let n be the length of the array a [0..n - 1] that you want to sort. Then the required number of exchanges performs the following algorithm:
for i from 0 to n – 1:
for j from 0 to n – 2:
if a[j] > a[j + 1]:
swap(a[j], a[j + 1])Let us prove it: for this we consider the following characteristic of the array, which is called the number of inversions: the number of pairs of positions (i, j) , where i < j and a [i]> a [j] . It is clear that in the sorted array the number of inversions is zero. On the other hand, the exchange of two neighboring elements can change the number of such pairs by no more than one. In this case, the sorting of the bubble during each exchange reduces the number of inversions by one.
Therefore, the number of exchanges in bubble sorting is equal to the number of inversions in the array, that is, the minimum number of exchanges that must be performed to sort the array.
Task D. Rails
An important parameter of the railway is the gauge - the distance between the two rails on which the train travels. It is this parameter that determines the types of trains and other cars that can travel by rail.
Recently, a space expedition to the planet RCC-0805 found out that there are railways on this planet too. It was even found the railway depot, but to determine the width of the track so far failed. The fact is that the railways on this planet fit without sleepers, therefore, it is not always easy to determine which rails correspond to each other.
The plan for the location of the rails in the railway depot is set. For simplicity, we assume that the territory is an infinite plane, and each rail is represented as a straight line. It is necessary to find the minimum width of the track d, at which the rails can be divided into pairs so that in each pair they are parallel and the distance between them is d.
Input Format
The first line contains an integer n (1 ≤ n ≤ 2000). Each of the next 2n lines contains four integers x i, 1, y i, 1, x i, 2, y i, 2 - the coordinates of two different points through which the rail passes. All coordinates do not exceed 1000 in absolute value. The straight lines corresponding to different rails do not coincide.
Output format
Print a real number - the minimum possible track width. It must be determined with an accuracy of no worse than 10 -6 .
If it is impossible to divide the rails into pairs with the requirements of the task at any track width, output the number −1.
Decision.
First, we divide the rails into equivalence classes in the direction of a straight line - parallel straight lines will fall into one class. After that, in each class we find all possible acceptable values of the gauge width for this class. The answer is the minimum possible distance that is suitable for all classes.
Now let's take a closer look at each of the stages of the solution.
To distribute straight lines by equivalence classes, we construct an equation for each of the straight lines. Let a straight line pass through points (x 1 , y 1 ), (x 2 , y 2 ). Then its equation of the form ax + by + c = 0 can be found as follows: a = y 1 - y 2 , b = x 2 - x 1 , c = - (ax 1 + by 1 ). It is now useful to normalize the coefficients of a straight line, dividing a, b and c by
 . Now, each line has two representations: up to multiplication of coefficients by –1. In order for each straight line to have a unique equation, it is convenient to additionally require the conditions “a> 0 or (a = 0 and b> 0)”. When this requirement is fulfilled, parallel lines have the same pair (a, b). In this representation, it is also convenient to calculate the distance between the straight lines: for two parallel straight lines ax + by + c 1 = 0 and ax + by + c 2 = 0, the distance is | c 1 - c 2 |.
. Now, each line has two representations: up to multiplication of coefficients by –1. In order for each straight line to have a unique equation, it is convenient to additionally require the conditions “a> 0 or (a = 0 and b> 0)”. When this requirement is fulfilled, parallel lines have the same pair (a, b). In this representation, it is also convenient to calculate the distance between the straight lines: for two parallel straight lines ax + by + c 1 = 0 and ax + by + c 2 = 0, the distance is | c 1 - c 2 |.Consider the class of parallel lines. We sort them by coefficient c. Consider the first straight line - it is paired with one of the other straight lines of this class. Let's go through this line. Let the distance between them be d. Now we greedily build a partition of straight lines into pairs at a distance d. If this can be done, then d can be the gauge for this class. We will consider straight lines in ascending order c. If the next straight line c = c i and has no pair yet, then it should be parallel to it at distance d with c = c i + d. If there is such a line, we pair it with the line in question. The pairing can be implemented in linear time using the two-pointer method: it suffices to note that c + d also increases with increasing c.
Finally, consider looking for an answer: let there be lists of possible answers for each of the classes. Naturally, they are sorted in ascending order. Two such lists can be easily crossed in one pass. After completing the intersection of all the lists, in a time proportional to the sum of their lengths, we obtain an intersection list, the minimum element of which is the answer to the problem.
Let's analyze the running time of the algorithm. Class distribution is done in O (n). For a given class of size k, the construction of a list of admissible distances is performed in O (k 2 ) and its length does not exceed k. Therefore, the last step is performed in O (n), and the entire algorithm in O (n 2 ).
Problem E. Guess the number
Recently, in one popular social network appeared the application "Guess the number!". Its users are offered a game, at each of the levels of which it is necessary to determine the hidden number from some information about it.
In particular, at one of the most difficult levels, it is necessary to guess a rational number x (0 <x <1), which is known that as a result of multiplying by a natural number k, exactly one change occurred in its decimal notation - the i-th one changed places in it and the j-th digit after the decimal point (the digits are numbered from one in the direction from left to right). At the same time, the digit to the decimal point has not changed, that is, the inequality 0 <k x <1 is fulfilled. Note that there can be infinitely many digits after the decimal point in the decimal notation x.
Your task is to write a program that will determine the value of x by the numbers i, j, k.
Input Format
The first line contains three integers i, j, k (1 ≤ i <j ≤ 1000; 2 ≤ k ≤ 109).
Output format
If the desired number exists, then print two integers - the numerator a and the denominator b of an irreducible fraction specifying the desired number (a, b> 0). Otherwise, print the phrase NO SOLUTION.
Decision
Suppose that initially at the i-th position is the digit s, and at the j-th position - the digit t. Then, after multiplying by k, the number is equal to x - 10 –i s + 10 –i t – 10 –i t + 10 –i s. Therefore, the required number is a solution to the equation kx = x - 10 –i s + 10 –i t - 10 –i t + 10 –i s.
Note that in fact the solution does not depend on the specific values of s and t, but only on their difference: (k - 1) x = (10 –i - 10 –i ) (t - s). In addition, s <t. Therefore, it is enough to go through the difference (t - s) in the range from 1 to 9. For each value of the difference, we find the solution to the equation and check it: make sure that when the number is multiplied by k, the numbers on the i-th and j-th positions in the decimal record change in some places, and the integer part remains zero.
Validation is necessary because, due to transferences, the solution of the reduced equation may not correspond to the solution of the problem.
Answers to frequently asked questions
During the competition, participants could send questions to the jury. Some questions were met especially often, and we decided to answer them in this article.
Question: Should I send the source code or the compiled file for review?
Answer: send the source code for review. The checking system itself compiles the decision of the participant, the command lines are specified in the rules of the Russian Code Cup
Question: where should I enter the data?
Answer: data should be entered from the so-called standard input stream. This corresponds to keyboard input, if you run a program that reads data from the standard input stream without additional parameters, the input will be from the keyboard.
In this case, low-level keyboard input, like analyzing keystrokes or receiving operating system messages about keystrokes, is the wrong approach. Read should be "from the console."
Question: where should I enter the answer?
The answer must be output to the standard output stream (by default, it is sent to the screen). Again, do not try to do this with low-level tools.
Let us give examples of reading the standard input stream and writing to the standard output stream in all programming languages that are supported in the Russian Code Cup.
Java
For input, use the System.in stream. The most convenient tools for parsing Java input are the BufferedReader and Scanner classes. BufferedReader is faster in reading and allows you to quickly read a large amount of data in rows. The scanner is slower due to the use of regular expressions, but it makes it very flexible to parse the input string, for example, read one number from the input.
To read from the standard input stream using BufferedReader, you should write a line in the program:
BufferedReader in = new BufferedReader (new InputStreamReader (System.in));
To read from the standard input stream using Scanner, write the following line in the program:
Scanner in = new Scanner (System.in);
For output, use System.out. In this case, System.out is non-caching (immediately flushes its buffer), if you need to output a large amount of information, it is better to wrap it in a PrintWriter.
C ++
You can use scanf for typing in the classic C style. This function reads data just from the standard input stream.
Input through streams is done using the cin stream. By default, it is set to standard input. Note that input using streams is significantly slower than input using scanf, so the program may not be able to read large amounts of data.
Again, you can use classic printf or stream cout for output. All performance notes remain valid for them - printf is faster.
C #
Use the Console for input. Console.ReadLine () reads the next line of input. To parse it, use the split () method. Converting data into numbers is done by the class Convert.
Console should also be used for output. For example, to display the number x, you can write Console.WriteLine (x).
Python
You can use input or raw_input functions for input. You can also use the sys.stdin file descriptor, which is configured on the standard input stream.
For output, we recommend using print.
Perl
Input from standard input in Perl is done with the <> command. This command reads a string from a file and returns it.
For output, we recommend using print.
Php
Input from standard input in PHP is done from the STDIN descriptor. The next line can be considered, for example, the fgets command.
You can use print or echo for output.
When using various functions of reading a string, we also recommend that you carefully read the documentation and pay attention to whether the function returns a newline along with the string. In the jury's tests, all lines, including the last, end with a line break, testing is conducted under Windows 7, the combination adopted in Windows is used to translate a line consisting of characters with codes 13 and 10.
In addition, you should note that testing is done automatically. Therefore, you should not try to display various “invitations to input” or try to “decorate” the output. You must enter the data, solve the problem and output the data, clearly following the output format.
Question: Is the test correct in the example?
Answer: the test in the example is usually correct - it is checked by several people, including several people who solve problems without knowing them in advance. If it seems to you that the test example is incorrect, then read more carefully the condition, probably you understand something wrong.
If it still seems to you that the example is incorrect, include in the request a detailed description of why you consider the example incorrect, which answer is correct, what do you think is inaccurate or ambiguous.
Question: Is the 239th test correct in problem X?
Answer: most likely the test is correct. If you think the test is wrong, write why you think so. Just the question "is this a test right" is pointless to ask. - «» - , .
: , ?
: , .
!
Russian Code Cup
Source: https://habr.com/ru/post/119187/
All Articles