On the verge of augmented reality: what to prepare for developers (part 2 of 3)

This is a continuation (see Part 1 ) of the transcript of the report of the same name from the ADD-2010 conference.

In this part, we will discuss how to process data from sensors, namely: accelerometers, gyroscopes and magnetic compasses. And why in modern devices put all three types of sensors.

Gyroscope

So, the first sensor is a gyroscope.
')
You know that the phone has a gyroscope, and you need to write a program that processes data from it. Immediately remember what gyros? - well, some such:


A strongly unwound heavy body, on soft hinged suspensions, it preserves, no matter how you twist the object to which it is suspended, it retains its direction, and you can measure two angles of deflection relative to the local coordinate system, and understand how your device is oriented . So, it’s kind of like, corners should come to you:


If you put two such gyros in perpendicular planes, then you can get all three angles:

• roll (or pitch);
• yaw;
• and that's the angle of attack.

I do not know what you are used to, I personally expected this from a gyroscope, and I naively thought so - now, now I will quickly write a program that does all this.

Understanding the laughter in the hall

The thing is, this is what a gyroscope looks like that stands inside all mobile and similar devices:


Now I have here [shows WiiMote + WiiMotionPlus, used as a device for the presentation] works, and what I show is the data from the gyroscope so that the pointer runs.

Nothing rotating there, of course, not, especially fast and heavy. There is such a thing as some kind of garbage, sorry, which telebunka in a magnetic field here and there, like a pendulum.


Accordingly, when you have a rotation around the axis, which passes perpendicularly through this plane, the Coriolis force arises, it rejects this tele-bunking thing and you can, measuring how the capacity of this structure has changed, you can guess what the force is. If schematically - then it is. Here you have a small mass, which fluctuates so (vertically), you excite it:



If there is such a rotation (counterclockwise), then the Coriolis force arises, it begins to deviate there and, strictly speaking, such transverse oscillations arise, and you can measure it as a capacitor capacitance.

Who remembers this Coriolis force, it depends on the angular velocity of rotation, respectively, what happens is that your output from this device is not really angles, but angular velocities, despite the fact that this is called a gyroscope.


In order to get an angle in the one-dimensional case, we need to integrate - though the signal comes to us discrete, so this is such a simple summation. In the three-dimensional case, all this translates into quaternions, if you want to do all this at all, then quaternions do not need to be intimidated.


This is a projection of this angular velocity on different axes, and now, roughly for WiiMote, a picture from the Internet, so as not to get confused how to handle it all.


This is all well and good, but integrating, we accumulate a mistake. There is a shift, i.e. constantly something floats away from us. Here's how here, despite the fact that our device was in place, gradually the angle floats, and it seems that gradually, gradually the device turns. What is not good for our purposes, and in general somehow sucks.


Here is a picture from the Internet, there is an error, here - degrees per hour, how much is accumulated, and here there are different types of gyros. And it is clear that micromechanical, which put in our expensive devices, they are the most terrible in this regard.

Accelerometer

It is necessary to do something with this, in principle, the angles can be measured with an accelerometer. Moreover, in the beginning it was only with the help of him that they tried to measure these angles.

What is an accelerometer? This is some kind of small weight, roughly speaking, fixed on springs, and by the deviation of this small weight, by its equilibrium position, we understand what kind of force acts, and we measure this acceleration.


Here’s what this accelerometer looks like:


In fact, what does the accelerometer measure? You have an acceleration of free fall, there is some kind of own acceleration, the device can be moved with acceleration.
Accordingly, the accelerometer measures this vector here, and in projection on the local coordinate system of the device:


This is what the accelerometer gives you at the output. In the one-dimensional case, everything looks quite simple:

• you have a rotated local coordinate system;
• you have a free fall acceleration projection;
• accordingly, you can get the angle of rotation relative to the vertical, using such a simple function as arctg2.

You can of course use all sorts of arcsines and arcosines, just acrthangent-2 gives you all 360 degrees, without hemorrhoids.


Look, we have an angle from the accelerometer, if the device’s own acceleration is close to zero, and we are in a one-dimensional, uncomplicated case.

It turns out as - we have an accelerometer, and there is a gyroscope. And we need something that will give us a fairly accurate angle at the exit.

What is the problem of the accelerometer? The fact that he makes a wild noise. And it makes a noise at high frequencies.

I tried to visualize here, and if you visualize this vector, it oscillates so wildly there, although the device itself is absolutely at rest. Those. high-frequency, strong, and with a good amplitude. Just so it is impossible to use it too, it is necessary somehow cunning.

There are two standard approaches for doing this:

• The first is some kind of magic called Kalman filter.
• The second is the so-called complimentary filter, the exact equivalent in Russian, this is the “alpha-beta filter”.

The magic of Kalman. This is a very complex filter, to be honest, I do not understand it myself. Not one book was written about him, not one dissertation was defended. Its main feature is that it uses within itself, i.e. for filtering, both a measurement model of oneself and a device model. Accordingly, these models are multiparametric. And in order for your filter to work well, you need to find this bunch of parameters in some way.


It is used, for example, in airplanes, but there, all the physical characteristics of the aircraft have long been well studied, due to its aerodynamic and other characteristics. What are the characteristics of the phone, besides caught in someone's hand? It will be cool to twist there, it’s completely weird stuff ...

In principle, this filter works, nothing is clear here, but there is a ready implementation in C ++ using this link . Therefore, you can not even understand, put, and then all the magic is to choose these parameters.


If you think that this is not necessary, then you can dial the "Kalman filter for android" and see a lot of results, i.e. the device itself sends you raw data, it does nothing for you with it - fuck, torment the developer, you.


There is a much simpler filter, which is called just “alpha-beta”, which is that, let's say, well, let's continue to integrate, just with a small correction, let's add the angle that we get from the accelerometer.


Well, there is a small number of delta, the only parameter of this filter that must be selected. Why is it such an alpha-beta, sometimes it is also called some kind of "composite filter". Because this coefficient is large enough, it kills low frequencies, and this coefficient is small, it kills high-frequency noise. It turns out that you are killing the low frequency of the noise from the integration, and here you are killing the high frequency, the same noise that comes from the sensor itself.

How to choose this parameter, here, too, there is a rather simple formula: a la relaxation, if you now incorrectly measured the angle, then how much you have it will converge to the correct value. This time of tau is calculated approximately like this, and here the frequency with which you receive the signal from the sensors is usually a hundred times per second, as all modern devices now give.


Well, for example, if you have a coefficient, for example, in hundredths, you get every hundred seconds that in about half a second the device will approach the position in which it should be.

Here comes the video, in general, people are lazy, see how to compare these filters. See how people do - nothing is needed at all, enough camera. The people are trying to compare these filters, and understand which one is better. Muzychka is good, dudes are not so tense, so why mathematics, to see the difference between functions, etc. This is how it is. On the left - the “alpha-beta” filter, in the center - “pure calman”, and on the right - they invented some more of their own.



But in fact, this is not very visualization, because it is not very clear what the parameters are here, everything is very much dependent on the parameters. It can be seen that this “alpha-beta”, for example, is smoother, maybe due to the fact that the coefficient was not chosen very well, “Kalman” seems to be clearer ...

So, this filter, Kalmanovsky, originated in radar, in processing radar signals, because there, you send a wave, it comes back to you and you measure the distance by the delay time, and by the Doppler effect, which and-and-y ", measure the speed. Almost like ours, only we have angles, but the same, i.e. there is a quantity and a derivative of a quantity measured at one time. And then there it is necessary to filter out the noise as efficiently as possible, “Kalman” was invented for this. My mother has been engaged all her life in the secondary processing of radar signals. I, when I figured it out all this, implemented this complimentary filter, asked her:
- How did you filter? Do you understand Kalman filter? Can you explain it to me?
- Oh, yes, we have a separate institute there in Zhukovsky or somewhere else worked on these Kalman filters, all defended a bunch of theses ...
- How did you select the parameters?
- Well, purely experimentally, by eye, somehow ...
- HM interesting. And other filters, simpler, did not try to apply?
And then she gave me:
- Well, yes, we finally used the simplest "alpha-beta" filter, it works about the same, and computationally much easier.
There still Soviet computers stood, and this Kalman filter was very computationally expensive.

Well, in fact, this is an example, if you have to deal with this, do not rush to immediately nibble this Kalman granite, nibble something simpler first.

---

Moreover, there is one more setup here, how to move from the one-dimensional case to the three-dimensional one. Well, in fact, it is necessary to move on to quaternions, and about here everything is the same, they are integrated in quaternions, but such an adjustment is added ...


In essence, these are the angles of deviation of the vector, which you have now measured, the turn, to which we can calculate through the current rotation quaternion.

To calculate this, we have only two vectors ... it actually breaks into three cases:


If we have a device vertically, then you can adjust (shows two perpendicular deflection angles) in such angles. But we cannot get such an angle (rotation around the axis) from the acceleration of free fall. Well, and similarly considering the position of this device (shows two perpendicular horizontal orientations), we get that we can adjust each time only two angles of three. And each time, two different angles from three.


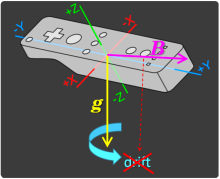
It turns out that all this works great, but there remains such a drift around the vertical axis. I can show you how the device I rotate now looks like this, we can put it in some orientation, at least something like this, although the table is moving ... now we will make a top view ... from what angle it is, now I I quickly rotate, an error accumulates, everything is bad, I put it, and here it is so hop, slightly corrected along those corners, and so it turned upside down, almost completely.

Those. Well, anyway, this is how an ambush turns out.

Magnetic compass

And here comes to the aid of a magnetic compass. If you noticed, many devices were not completed before, but now they have begun to shove him violently, it would seem - why?

Everyone remembers that we have a magnetic field around the Earth, respectively, we can measure the magnetic field strength, and we have a vector, additional and orthogonal to the acceleration of free fall!

We measure its projection on the device’s coordinate system, and here the acceleration of this very device no longer soars us, which is also a buzz. It turns out that we kill the drift around the vertical axis, i.e. using the projections of these two vectors, we can fully establish the position of the device in space (probably, we mean the orientation in space ).


That would seem such a simple task, but so many hemorrhoids.

You can look at an example of how different augmented reality programs are working now, they are now working quite crap, to put it mildly, and here's why.

Therefore, the magnetic compass is very important, and buying a device, if you want to use it so, pay attention to its presence.

Cameras

Let's go to the cameras ...

And why they do not use the level, the usual?

Just how to stuff it into a mobile phone? Why not use a conventional gyro - unwind it and that's it ( sarcasm detected ).

And you can make a small level ...

Well, it will be one angle relative to the horizon. And also it will be very fonit, in principle, the accelerometer will give you the same thing, the same as the level, if you think about it. Accelerometer is essentially the level.

... drift ... can also give, rotation around the axis ...

No, not very clear. Level does not track it.

Let's move on ... a lot more I just want to tell ... in fact, sensors, sooner or later they will figure it out, there are all sorts of SDKs in which these problems are solved, and I think one way or another, in a year or two it will also be easy working as with a mouse will be a ready class from which it will be possible to inherit or use it and not know about all these pitfalls.

Much more interesting and innovative is the processing of video images that we receive from cameras.

To be continued

• part 3

Acknowledgments

Once again I want to thank Stas Fomin ( belonesox ) for the transcript. Stas, among other things, is the permanent chairman of the Program Committee of Conferences of the Application Developer Days series and, in my opinion, did much more for this conference than its direct organizers, although he does not receive a penny for it. For example, for the next conference in Peter, Stas was going to take a bunch of additional equipment (additional projectors, monitors, video cameras, all kinds of adapters to connect any laptop to any projector or plasma, etc.) on his hump from Moscow - and all this so that he himself would not be ashamed of the conference, the creation of which he has the most direct relation to.

If you like this material, thank belonesox karma or / and visit one of the events in the organization of which Stas takes part.