Challenger for the theory of everything - E8 geometry

Unified Geometric Theory - Part 1

Theories of unification of interactions

In fact, the question of the theory of everything or the theory of combining all fundamental interactions (electromagnetic, weak, strong, gravitational, by the way the first three lend themselves to the current theories of unification) into a unified theory is probably one of the main issues of modern theoretical physics. This article will discuss the candidate for a solution to this issue, namely, the unified geometric theory of E8. What is it?

But first, let's follow the path to the great union. The first theory of interaction was the theory of electromagnetism, created by Maxwell. Then Einstein formulated the general theory of relativity, describing the gravitational field. An idea emerged to build a unified theory of fundamental interactions (of which only two were known at the time), just as Maxwell managed to create a general description of electrical and magnetic phenomena. Such a unified theory would unite gravity and electromagnetism as particular manifestations of a certain unified interaction.
With the advent of quantum mechanics, the task became more complicated, because the common effects of these two theories could not be combined within the framework of one theory.
Later, the nature of both weak and strong interaction was clarified. In 1967, Salam and Weinberg created the theory of electroweak interaction, combining electromagnetism and weak interactions. Later in 1973, the theory of strong interaction was proposed (quantum chromodynamics). On their basis, the Standard Model of Elementary Particles was constructed, describing electromagnetic, weak and strong interactions. At the moment, the Standard Model is a generally accepted theory for describing interactions.

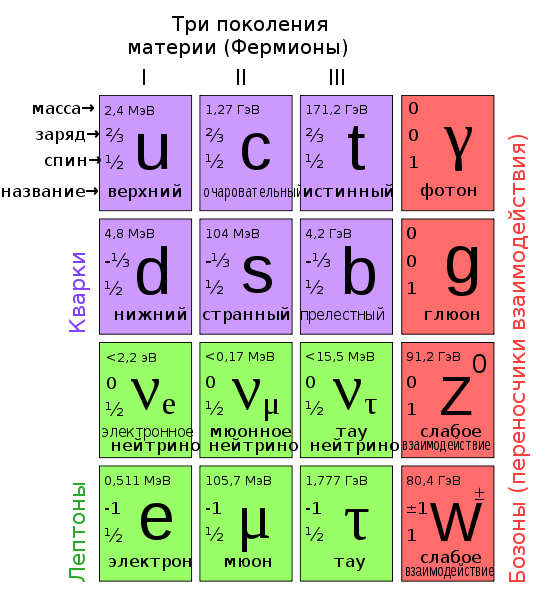
The question arose: how to combine the theory of gravity and the Standard Model. This question remains open. There are many assumptions about how to solve this problem. String theory, M-theory, loop quantum gravity, superstring theory, as well as considering today the theory of E8.

Single geometric object

It can be assumed that at the micro level all interactions and their carriers are a kind of complex universal geometric object.
To continue the conversation we will try to make out the concepts of the geometry of fundamental interactions that we need.
')

Groups

Consider a fairly simple example that illustrates the concept of a group and then a Lie group. Lie groups were created in the theory of Lie algebra by the Norwegian mathematician Sophius Lee. It is worth saying that the Norwegian mathematicians made a huge contribution to the development of group theory. Let's go back to the example. Under our analysis will get the simplest geometric shape - a square. Consider a 90 degree rotation of the square in the plane of the figure itself. We will turn the n-th number of times, we note here the fact of symmetry of our transformations.

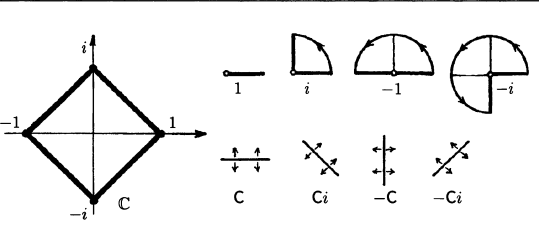
Turns will be described using complex numbers as in the figure. And accordingly, let us associate the vertices with the complex numbers 1, i, -1, -i, then to the rotation by 90 degrees we will compare the multiplication by i. The degrees of the number i will be our turns. All we can get four different points of the plane, we have four elements. Multiplying any two of them will produce a result, which is also one of these four elements. It is these four degrees of the number i that can serve as an example of a finite group. The group is also determined by the rule of multiplication of elements a a (bc) = (ab) c. The existence of a single element and an inverse element is required. If we add here the commutative property of multiplication ab = ba, then such a group is called an abelian group (by the way Abel is also a Norwegian mathematician). Our group is obviously abelian, since complex numbers have the commutative property of multiplication.
Now we introduce a reflection operation that changes the orientation of our square, namely, a rotation around an axis to which the complex conjugation — C — corresponds algebraically. The following relations will obviously be true:
Ci = -iC, C (-1) = (- 1) C, C (-i) = iC, CC = 1 => i ^ 4 = 1, C ^ 2 = 1 Ci = i ^ 3C
From the latter, it can be noted that with respect to the operation of complex conjugation, this group is not abelian.
If we consider the sphere and its rotation, then we get an infinite number of different configurations, since we can rotate it at any angle, getting all the same object symmetric to the original. Such a group is called a continuous or Lie group.
A Lie group is very important for understanding the geometry of fundamental interactions.

General considerations and introductory word

In 2007, the physicist Anthony Garrett Lisi wrote an article that became the subject of wide discussion among theoretical physicists.
Many modern scientists believe that an attempt to combine Einstein's theory of relativity and quantum theory should radically change our understanding of reality. However, in contrast to them, Lisi believes that the geometric description of modern quantum physics can be extended to include a gravitational theory, leading to the creation of a long-awaited unified theory of all interactions.
Why geometry? The question is the place to be. We will try to answer it. In order to explain the essence of the E8 theory, we need knowledge of some widely used geometrical principles that govern all known particles and interactions. Geometry studies forms. However, as applied to the problems of fundamental physics, each of us may ask what forms it is. Plato presented the main elements - earth and air - as small cubes and octahedra (octahedra). Similarly, in modern physics, geometric objects associated with elementary particles are regular shapes that exist, as it were, in some abstract imaginary space. Of course, we cannot see these figures — they belong to the mathematical space — but we have been given to reveal the effects caused by them already in our real world. A direct analogy with the geometric conceptual apparatus allows you to operate on time-consuming things easier and faster.

Geometry of the Standard Model

The basic geometric idea underlying the Standard Model is that each point in our space-time is associated with certain forms, called fibers. Each layer corresponds to its type of particles. For clarity, our universe can be represented as a terracotta figurine, completely covered with sprouts. Its entire surface is an analogue of our four-dimensional space-time, and the processes are layers. The entire figure as a whole - our real space – time and layers – processes — is called the multidimensional fiber bundle space. The layers obviously lie outside our space; mathematically they are external spaces “attached” to each point of our ordinary space, and have different forms depending on the properties of the particles.

This graphic geometric concept, first proposed in 1918 by the mathematician Hermann Weyl , has now become a well-established physical principle. The layers of outer space differ from the assumed spatial dimensions of the string theory, having a fixed shape. Their dynamics are determined by the method of attachment to our four-dimensional world.

Electromagnetic interference

Consider, from the point of view of geometry, electromagnetic interaction. The electromagnetic field is present everywhere, this fact is due to the fact that the shape of the layers is a circle.

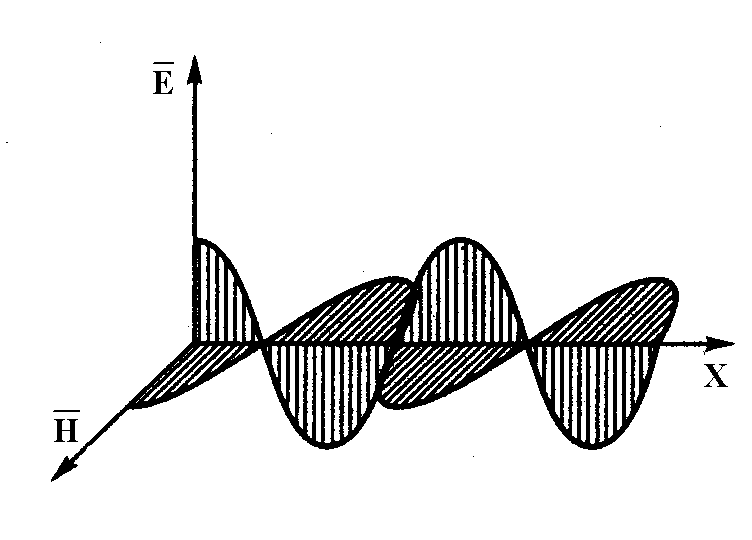
Projecting on one axis, we really get a semicircle. In the framework of this approach, we get some circles that twist around the beam.

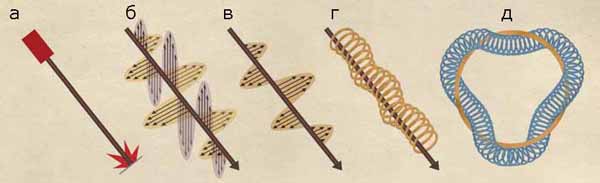
They have a symmetry called U (1), and is the simplest example of a Lie group. A circle has a single family of symmetries: when it turns around its center, it passes into itself, without changing. The rotation of a circle around its center at a small angle is called a Lie group generator. By following the generator as indicated by the compass needle, arbitrary rotations around the center can be made.
The space of the bundle for electromagnetic interactions is a circle, "attached" to each point of our real space-time. It is important to note that each circle can rotate at small angles relative to its space – time “neighbors”. The so-called connectivity field for a bundle space describes how adjacent layers are connected through their symmetrical turns. The fields of electrical and magnetic interactions fill space – time according to the curvature of their layers; in other words, the electric and magnetic fields follow the rotation of circular layers in space – time. An electromagnetic wave is a wave-like oscillations of the indicated circles in space – time. One quantum of an electromagnetic wave (photon) is a propagating particle of light.
Each type of elementary particles corresponds to a different layer in space – time. The figures mentioned by us have many different types of processes. So, everything in the world electrons come from the rotation of a layer of the same type - which, in particular, explains why all electrons are the same. The layers of electrically charged particles, such as an electron, turn around circular layers of electromagnetic interactions like filaments around a screw. The speed of rotation of a layer corresponding to a particle around a circle is equivalent to the electric charge of this particle, i.e. characterizes the degree of its interaction with the electromagnetic field.
Since the revolutions around the circle have a periodicity, the charges of the corresponding particle are integers multiplied by a certain standard unit of electric charge. Among elementary particles of matter, called fermions, electrons have an electric charge of –1 (three full turns), upper quarks have an electric charge +2/3 (two opposite turns), lower quarks have an electric charge –1/3 (one turn) and neutrino - 0. Antimatter particles, such as positrons and antiquarks, rotate around the electromagnetic circle in the opposite direction, which gives these particles an opposite electrical charge.
In a collision, particles can be transformed into particles of other types, but their total electromagnetic charge does not change before and after the interaction. This important property can be interpreted as a consequence of the geometry of the layers: when any two particles meet, their turns are added. Thus, the picture of the space of the bundle well explains what we know about electromagnetism. Electric charges describe the geometric structure of the total electromagnetic field and the separation space for a substance, determining which interactions are possible between electrically charged particles.

That's all for today. Finally a few videos.



PS In the second part, we consider gravity as a geometric object. And also we will see a refutation of this theory in a popular science context.

Based on:
1. "In the World of Science" №3 2011
2. Penrose R. “The Path to Reality or the Laws Governing the Universe”