Calculate editorial distance

The distance, or Levenshtein distance, is a metric that allows determining the “similarity” of two lines — the minimum number of operations to insert one character, delete one character, and replace one character with another, necessary to turn one line into another. The article presents a method for calculating the editorial distance when using a small amount of memory, without significant loss of speed. This approach can be applied for large lines (of the order of 10 ⁵ characters, i.e., actually for texts) when receiving not only the “similarity” estimate, but also the sequence of changes for translating one line to another.

Slight formalization

Suppose there are two lines S ₁ and S ₂ . We want to translate one into another (even if the first to the second, it is easy to show that the operations are symmetrical), using the following operations:

• I: Insert a character in an arbitrary location;
• D: Delete a character from an arbitrary position;
• R: Replacing a character with another.

Then d (S ₁ , S ₂ ) is the minimum number of I / D / R operations for translating S ₁ into S ₂ , and the editorial prescription is listing the operations for translating with their parameters.

The task is easily solved by the Wagner – Fisher algorithm, but to restore the editorial prescription, O (| S ₁ | * | S ₂ |) memory cells will be required. In brief, I present the algorithm itself, since the “optimization” is based on it.

Wagner-Fisher Algorithm

The desired distance is formed through the auxiliary function D (M, N), which finds the editorial distance for the substrings S ₁ [0..M] and S ₂ [0..N]. Then the full editorial distance will be equal to the distance for full-length substrings: d (S ₁ , S ₂ ) = D _{S 1 , S 2} (M, N).
')
The self-evident fact is that:

D (0,0) = 0.

Indeed, the blank lines match.

Also, the implications for:

D (i, 0) = i;
D (0, j) = j.

Indeed, any line can turn out to be empty, adding the necessary number of necessary characters, any other operations will only increase the estimate.

In general, a little more complicated:

D (i, j) = D (i-1, j-1), if S ₁ [i] = S ₂ [j],
otherwise, D (i, j) = min (D (i-1, j), D (i, j-1), D (i-1, j-1)) + 1.

In this case, we choose which is more profitable: delete the character (D (i-1, j)), add (D (i, j-1)), or replace (D (i-1, j-1)).

It is easy to understand that the algorithm for obtaining the estimate does not require memory of more than two columns, the current (D (i, *)) and the previous one (D (i-1, *)). However, the full matrix is ​​needed to restore the editorial prescription. Starting from the lower right corner of the matrix (M, N) we go to the upper left, at each step looking for the minimum of three values:

• if the minimum is (D (i-1, j) + 1), add the deletion of the symbol S ₁ [i] and go to (i-1, j);
• if the minimum is (D (i, j-1) + 1), add the insertion of the character S ₁ [i] and go to (i, j-1);
• if it is minimal (D (i-1, j-1) + m), where m = 1, if S ₁ [i]! = S ₂ [j], otherwise m = 0; then go to (i-1, j-1) and add a replacement if m = 1.

Here (i, j) is the cell of the matrix in which we are at this step. If two of the three values ​​are minimal (or all three are equal), this means that there are 2 or 3 equivalent editorial guidelines.

As a result, you need O (| S ₁ | * | S ₂ |) time and O (| S ₁ | * | S ₂ |) memory.

General arguments

A prerequisite for the creation of this method is a simple fact: in real-world conditions, memory is more expensive than time. Indeed, for lines with a length of 2 ¹⁶ characters, you need about 2 ³² computational operations (which at current capacities will fall within ten seconds of calculations) and 2 ^{32 of the} same memory, which in most cases is already larger than the physical memory of the machine.

The idea of ​​how to use linear memory (2 * | S ₁ |) to estimate the distance lies on the surface, it remains to transfer it correctly to the calculation of the editorial prescription.

Counter calculation method (Hirschberg algorithm)

We will use recursion to split the task into subtasks, each of which does not require a lot of memory. For further sketches take some initial values ​​of the lines.

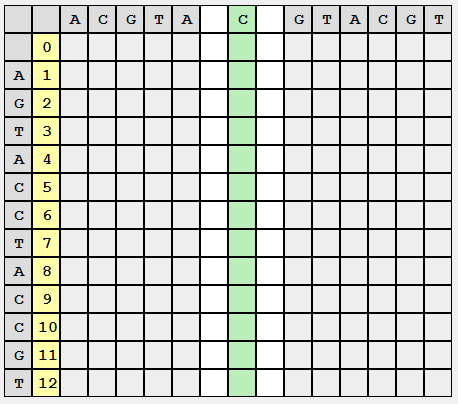
S ₁ = ACGTACGTACGT,
S ₂ = AGTACCTACCGT.

Looks like, isn't it? But rewriting one into the other "by eye" is not so obvious. The letters, by the way, were not chosen by chance - they are nitrogen bases (A, T, G, C), DNA components: the editorial distance estimation method is actively used in biology to evaluate mutations.

Then the initial blank matrix will look (exactly look, we will store only the necessary data) as follows:



In each cell should be the value of the editorial distance.

We divide the original task into a subtask, divide the second line into two equal (or almost equal) parts, remember the place of splitting, and begin to fill in the matrix exactly the same way as did Wagner-Fisher:



When filling, we will not store the previous columns, moving from left to right, top to bottom, as the values ​​of D (i, j) are calculated, the values ​​of D (i-1, j) can be deleted:



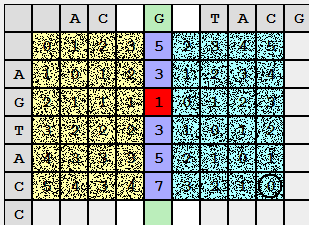
Similarly, fill in the right side of the partition. Here we will move from right to left, from top to bottom:



So we met. Now you can get a part of the solution to the general problem by combining the private ones Sum up the values ​​in the left and right columns and select the minimum.



What does this combination mean? We tried to combine the first row with the first half of the second row, then the first row with the second half of the row. The sum allows you to get the number of operations to change the first line to bring it to the concatenation of the first and second half of the second line (that is, the second line) ... this means that we got the value of the editorial distance! But it’s too early to rejoice, because this result could have been achieved even easier (the method described above).

However, looking at the picture from a different angle (literally), we got another significant fact: now we know how to cut the first line into two halves so that the corresponding pairs give us the editorial distance: d (S _{1 1} , S _{2 1} ) + d (S _{1 2} , S _{2 2} ) = d (S ₁ , S ₂ ). A row (in the matrix) in which the minimum is located and there is the required partition S ₁ , and this partition is sent to issue an editorial instruction.

Similarly, we will divide the task already for the resulting substrings S _{1 1} and S _{2 1} (and we will not forget the second pair either):



We finish the division when there is no single substring S _{1 of} length greater than 1.



We obtain a list of partitions, where each substring S ₁ (look vertically) gives a minimal estimate of changes relative to the corresponding substring S ₂ (horizontally).



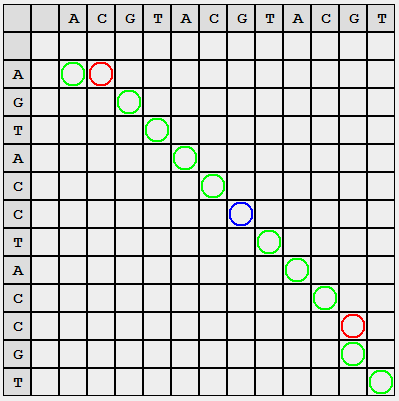
For convenience, I colored the marks with colors: green means symbol-by-word matching of lines in selected positions, blue needs replacing, and red means deleting or adding. It is easy to see that the “red” circles are in the same row / column (a little attentive task: explain what this means).

In a more convenient form, the result can be written as follows (the red dashes are the correspondence of symbols, the shifts are indicated by black horizontal ones):

Algorithm analysis

Memory: for each step, you will need to memorize no more than one column d (i, *) and a set of partitions S ₁ . Total O (| S ₁ | + | S ₂ |). That is, instead of a quadratic volume, we get a linear one.

Time: each partitioning of S [0..N] by column t generates the processing of substrings S [0..t] and S [t..N]. The total number of partitions is N. When processing each partition (S ₁ [i..j], S ₁ [k..n]), (j - i) x (n - k) operations are required. Summing up the worst-case estimate for substrings, we end up with 2 * | S ₁ | * | S ₂ | operations. The running time of the algorithm remains quadratic, although the multiplicative constant has changed.

So, we solved the problem using a linear amount of memory and slightly lost in speed, which in this case can be considered a success.

[*] Wikipedia: Hirschberg algorithm .