Introduction to F #, the blue pill
[ Previous post ]

That's the expected, or not, continuation. Today we will swallow the blue pill, which proudly personifies FP (functional programming), and dive into the functional part of F # even deeper. Let's talk about functions, recursion, pattern matching, and a few more interesting things. Interesting? Then swallow the pill and begin to dive.

First I would like to talk about the origins of FP, about the λ-calculus. After all, this mathematical theory created by Alonzo Church formed the basis of functional programming. I will not give a long and tedious lecture on mathematics, I will just tell you briefly. In the end, then you can surprise someone with your knowledge not only in F #, but also in its mathematical background. What, in fact, is this terrible name λ-calculus? In that Church wanted to generalize mathematics so that absolutely everything can be represented as one of the fundamental concepts - functions. Moreover, his theory suggests that everything is a function. "What's the problem? Why not use the existing notion of a function? ”The reader will ask. The fact is that the mathematician wanted to use functions everywhere and everywhere, and, often, it is inconvenient for them to give a name, as we were all taught in schools / institutes:
Then Alonzo came up with a notation that allows you to write a function without assigning a name to it:
In this case, the function is absolutely identical to the previous example, except that it does not have a name. It can also pass the value of the argument to it:
It is also possible to pass another λ-function to the parameters of the λ-function. I think a direct analogy with the lambda functions, which we met in the previous article, is clearly visible.
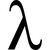
And I’m almost done with math. Nearly. After all, everyone knows what is recursion? Well, fine. Now we will write a recursive function (calling itself) to calculate the Fibonacci numbers. Fibonacci numbers - a sequence of numbers, where each subsequent number is equal to the sum of the previous ones:
If we write it in the language of functions, then the function that returns the Fibonacci number by its number in the sequence will look like this:
And on F # like this:
There are two new keywords that you should pay attention to:
What happens inside the function? In fact, everything is very simple: if the argument n is 1 or 2, then we return 1, otherwise we return the sum of the two previous numbers in the sequence. In fact, match provides much more possibilities, but we will return to it a little later, and for a start we will consider the main types in F #.
')

In order to declare your type you must, oddly enough, use the type keyword. So far, we cannot declare anything sensible, so we simply redefine the int:

A tuple, or tuple, is a kind of composite type in F #. In order to quickly understand what and how we consider examples:
As you can see from the example, a tuple is a combination of two or more types (not named but ordered). point2d and point3d represent points on 2-dimensional and 3-dimensional planes, personAndId is the name and id. For the convenience of working with tuples in the standard F # library, there are two functions: fst and snd, which return the first and second elements of the tuple, respectively. How to get the third item?
Here is an example of a type-tuple declaration:

Of course, this is not about records. Records are another structural unit of F #. They differ from tuples in that each field of the record has a name; the content can still be anything. Consider the syntax:
I think no explanation needed.

The next structural unit is associations. They allow you to combine data in different ways. Here is an example of a simple merge:

Now that the reader already knows a lot about the basic structural units of F #, we can talk more in detail about pattern matching. Match is somewhat similar to a switch from imperative and OO languages, only it provides much wider opportunities. The only limitation is that templates should cover the whole range of possible values. I want to note that it seems inconvenient and absurd only at first.
A more complete description can be found here .

Suppose we need an implementation of a binary tree that has a type, that is, a tree of strings, a tree of ints, etc. Types in F # can be generalized, it is done this way:
Yes, a generic binary tree on F # looks just like that.

Well what can I say, I hope, I tried not in vain, and this post will also appeal to many. Next time we’ll continue to swallow the blue pills, talk about lists and sequences, currying functions and much more. Thank you for reading.
First of all, msdn , there you can find a more detailed description of much of what was discussed today.
Secondly, Functional Programming for the Real World (Tomas Petricek, Jon Skeet) is a book for those who are used to an imperative approach to solving problems. Some examples from this post have been partially taken from there.
In fact, the code that was provided in the post above is terrible. But, but it is simple to understand. And for those who want to see a more functional approach, I will give a more competent example (thanks, onikiychuka ):
As mentioned above, we will analyze such functions in more detail next time.
Type expressions
also represent a pattern matching mechanism. Thank you, jack128 and onikiychuka .
Introduction

That's the expected, or not, continuation. Today we will swallow the blue pill, which proudly personifies FP (functional programming), and dive into the functional part of F # even deeper. Let's talk about functions, recursion, pattern matching, and a few more interesting things. Interesting? Then swallow the pill and begin to dive.
Immersion

First I would like to talk about the origins of FP, about the λ-calculus. After all, this mathematical theory created by Alonzo Church formed the basis of functional programming. I will not give a long and tedious lecture on mathematics, I will just tell you briefly. In the end, then you can surprise someone with your knowledge not only in F #, but also in its mathematical background. What, in fact, is this terrible name λ-calculus? In that Church wanted to generalize mathematics so that absolutely everything can be represented as one of the fundamental concepts - functions. Moreover, his theory suggests that everything is a function. "What's the problem? Why not use the existing notion of a function? ”The reader will ask. The fact is that the mathematician wanted to use functions everywhere and everywhere, and, often, it is inconvenient for them to give a name, as we were all taught in schools / institutes:
f(x) = x - 5
f(6) = 6 - 5 = 1
Then Alonzo came up with a notation that allows you to write a function without assigning a name to it:
λx.x-5
In this case, the function is absolutely identical to the previous example, except that it does not have a name. It can also pass the value of the argument to it:
(λx.x - 5) 6 = 6 - 5 = 1
It is also possible to pass another λ-function to the parameters of the λ-function. I think a direct analogy with the lambda functions, which we met in the previous article, is clearly visible.
“Stop carrying nonsense! More code. ”
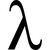
And I’m almost done with math. Nearly. After all, everyone knows what is recursion? Well, fine. Now we will write a recursive function (calling itself) to calculate the Fibonacci numbers. Fibonacci numbers - a sequence of numbers, where each subsequent number is equal to the sum of the previous ones:
Fib = {0, 1, 1, 2, 3, 5, 8, ...}
If we write it in the language of functions, then the function that returns the Fibonacci number by its number in the sequence will look like this:
f(n) = f(n - 1) + f(n - 2)
f(1) = 1
f(2) = 1
And on F # like this:
let rec fib n = match n with | 1 | 2 -> 1 | n -> fib(n-1) + fib(n-2) There are two new keywords that you should pay attention to:
- rec indicates that the function is recursive
- match, with is a pattern matching mechanism, for familiar c C # or C / C ++ pattern matching can be thought of as a kind of switch on steroids
What happens inside the function? In fact, everything is very simple: if the argument n is 1 or 2, then we return 1, otherwise we return the sum of the two previous numbers in the sequence. In fact, match provides much more possibilities, but we will return to it a little later, and for a start we will consider the main types in F #.
')
Type declaration

In order to declare your type you must, oddly enough, use the type keyword. So far, we cannot declare anything sensible, so we simply redefine the int:
type myInt = int Tuples

A tuple, or tuple, is a kind of composite type in F #. In order to quickly understand what and how we consider examples:
// int*int; * - let point2d = (10, 5) // int*int*int let point3d = (1, 1, 2) // string*int let personAndId = ("Some Name", 3) let x2d = fst point2d let y2d = snd point2d As you can see from the example, a tuple is a combination of two or more types (not named but ordered). point2d and point3d represent points on 2-dimensional and 3-dimensional planes, personAndId is the name and id. For the convenience of working with tuples in the standard F # library, there are two functions: fst and snd, which return the first and second elements of the tuple, respectively. How to get the third item?
// ; _ , / let third (_, _, t) = t Here is an example of a type-tuple declaration:
// -; string, int type personAndId = string*int // personAndId; : , let person:personAndId = ("Habr", 1) Records aka records

Of course, this is not about records. Records are another structural unit of F #. They differ from tuples in that each field of the record has a name; the content can still be anything. Consider the syntax:
type person = {name : string; surname : string; id : int} let sampleUser = {name = "Habra"; surname = "Habr"; id = 1} let sampleUserName = sampleUser.name I think no explanation needed.
Discriminated unions, or tagged unions

The next structural unit is associations. They allow you to combine data in different ways. Here is an example of a simple merge:
type Currency = | Liter of float | Pint of float let liter = Liter 5.0 let pint = Pint 10.0 Pattern matching, or pattern matching

Now that the reader already knows a lot about the basic structural units of F #, we can talk more in detail about pattern matching. Match is somewhat similar to a switch from imperative and OO languages, only it provides much wider opportunities. The only limitation is that templates should cover the whole range of possible values. I want to note that it seems inconvenient and absurd only at first.
// , let isOdd n = (n % 2 = 1) // , 1 3 let oneToThree n = match n with | 1 -> printfn "One" | 2 -> printfn "Two" | 3 -> printfn "Three" // ; _ n | n -> printfn "Geather than three" // type Point = int * int // matching' let findZero point = match point with | (0, 0) -> printfn "x = 0 and y = 0" | (0, y) -> printfn "(0, %d)" y | (x, 0) -> printfn "(%d, 0)" x | _ -> printfn "x <> 0 and y <> 0" type Person = | NameOnly of string | IdOnly of int // - | IdAndName of string * int // matching' let personInfo person = match person with | NameOnly(name) -> printf "Name is %s" name | IdOnly(id) -> printf "Id is %d" id | IdAndName(name, id) -> printf "Name is %s and Id is %d?" name id // matching'a let matchWithCondition x = match x with | x when x >= 5. && x <= 10. -> printfn "x is between 5.0 and 10.0" | _ -> () A more complete description can be found here .
Generic types

Suppose we need an implementation of a binary tree that has a type, that is, a tree of strings, a tree of ints, etc. Types in F # can be generalized, it is done this way:
// ' type 'a BinaryTree = // , - | Node of 'a BinaryTree * 'a BinaryTree | Value of 'a (* : type BinaryTree<'a> = | Node of BinaryTree<'a> * BinaryTree<'a> | Value of 'a *) // , , let tree1 = Node( Node (Value 1, Value 2), Node (Value 5, Value 100) ) let tree2 = Node( Node (Value "Binary tree", Value "in F#"), Node (Value "is so", Value "Simple") ) Yes, a generic binary tree on F # looks just like that.
Conclusion

Well what can I say, I hope, I tried not in vain, and this post will also appeal to many. Next time we’ll continue to swallow the blue pills, talk about lists and sequences, currying functions and much more. Thank you for reading.
What to read
First of all, msdn , there you can find a more detailed description of much of what was discussed today.
Secondly, Functional Programming for the Real World (Tomas Petricek, Jon Skeet) is a book for those who are used to an imperative approach to solving problems. Some examples from this post have been partially taken from there.
For those who were few
Fibonacci
In fact, the code that was provided in the post above is terrible. But, but it is simple to understand. And for those who want to see a more functional approach, I will give a more competent example (thanks, onikiychuka ):
let fib = Seq.unfold (fun state ->Some(fst state + snd state, (snd state, fst state + snd state))) (1,1) fib |> Seq.take 20 As mentioned above, we will analyze such functions in more detail next time.
Pattern matching
Type expressions
let second (x, y) = y let getValueFromOption (Some value) = value also represent a pattern matching mechanism. Thank you, jack128 and onikiychuka .
Source: https://habr.com/ru/post/116904/
All Articles