Polygon Fill Algorithms
Today I read an interesting article on pouring algorithms and decided to add it a little. If the original article talked about filling in arbitrary areas, then we'll talk about the private, but more common, case of filling polygons.
In this topic, we will look at three groups of algorithms:
Using this algorithm, you can paint over any closed areas. The source data for this algorithm is the color of the area border and the point belonging to this area (the so-called bare pixel). The essence of the method is as follows: we take a bare point and paint it. For each unpainted neighbor, we perform a similar procedure. So we get a recursive algorithm, which is described below in pseudocode:
Of course, you can use both four- and eight-connected neighborhoods.
This algorithm has more disadvantages than advantages: it is slow and consumes a lot of memory for the stack, so it would be much more correct to proceed to the next group of algorithms.
This algorithm is suitable only for those cases when the region to be painted can be specified as a polygon. We assume that we work with a polygon with vertices P1, P2, ..., PN, P1 and want to display it on the screen along with all internal points. For convenience, we assume that each edge of a polygon is defined by the coordinates of its ends x1, y1 and x2, y2 (with y2≥y1). We also agree that the x coordinate increases when moving from left to right, and the y coordinate when moving from top to bottom.
The overwhelming majority of algorithms for rasterizing polygons are based on the following assumption: any cutting straight line intersects the polygon boundary even number of times. This statement is false only in two cases:
These two cases are fairly easy to detect, so when considering the algorithms for rasterizing polygons, we assume that the above assumption is always true.
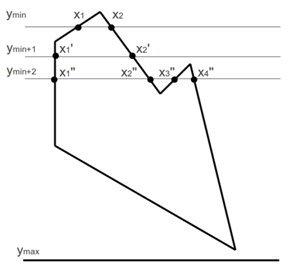
The algorithm based on the list of edge points consists of three main steps:
At the first stage, all non-horizontal edges of the polygon are rasterized. For each value of y, a list of x-coordinates shaded during rasterization is compiled. For example, for the polygon under consideration, we obtain the following values (when moving clockwise):
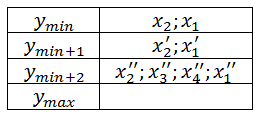
At the second stage, for each value of y, the lists are ordered in ascending order. After that, the lists will look like this:

At the third stage, for each y, all the obtained segments are filled.
The advantage of this algorithm is that each pixel is processed strictly once. So It can be argued that this algorithm is suitable for devices where access to video memory takes a relatively long time.
There is a modification of this algorithm, optimized for memory consumption. In it, at each step, only those edges are processed that intersect with the current scan line.
This method of rasterization of polygons is based on the properties of the logical exclusive-OR (XOR) operation.

This algorithm, like the algorithm with a list of edge points, begins with rasterization of the boundaries. After the borders are drawn, the fill is reduced to filling in each line the gaps between the two filled dots.
Imagine the image as a binary array I. We agree that I [x; y] = 1 when the pixel is shaded, and I [x; y] = 0 when the pixel is not shaded. It is easy to see that applying the operation I [x + 1, y] = I [x; y] XOR I [x + 1; y] to all pixels in a row will lead to an almost perfect result. As a result of this operation, all gaps will be painted over, but the last pixel in each gap will not be painted over. In most cases, this error is insignificant and inconspicuous, but if you want to get an accurate result, you can re-display the border after the completion of the algorithm, or use a small modification of this algorithm.
The advantage of this algorithm is its extreme simplicity and high speed. The disadvantage is that the algorithm cannot work if there are extraneous images.
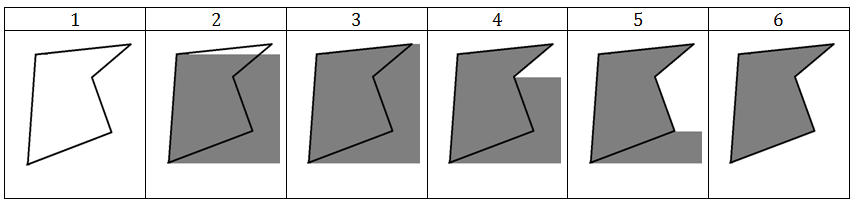
The XOR method for faces is described by the following simple algorithm: For each edge in the polygon, the colors of all the pixels located to the right of this edge are inverted. In this case, the order of traversing the edges does not matter. The table shows the steps of this algorithm (clockwise):
The disadvantage of this algorithm is high time costs, since some pixels are processed more than once. In addition, the greater the distance from the image to the right border of the screen, the more unnecessary operations will be performed.
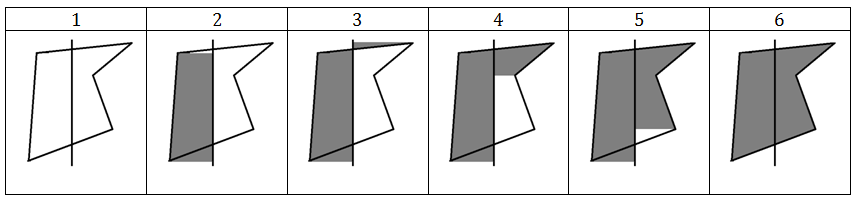
A modified version of the XOR algorithm for faces is free from some of the drawbacks. It is called the XOR algorithm for partitions with a partition. His idea is to invert the area not between the edge and the border of the screen, but between the edge and the special vertical lines (the so-called partition). Most often the partition is carried out so that it intersects the polygon. The steps of the algorithm are given in the table.
In this topic, we will look at three groups of algorithms:
- Fill algorithm with priming
- Edge Point List Algorithms
- XOR Algorithms
Fill algorithm with priming
Using this algorithm, you can paint over any closed areas. The source data for this algorithm is the color of the area border and the point belonging to this area (the so-called bare pixel). The essence of the method is as follows: we take a bare point and paint it. For each unpainted neighbor, we perform a similar procedure. So we get a recursive algorithm, which is described below in pseudocode:
1. Put a seed pixel onto the stack ;
2. Extract pixel from stack ;
3. Assign the required value to the pixel ( color of the inner area ) ;
4. Each neighboring pixel is added to the stack, if it is
4.1. It is not a boundary ;
4.2. Not previously processed ( i.e. its color is different from the color of the border or the color of the inner region ) ;
5. If the stack is not empty, go to step 2.6.
Of course, you can use both four- and eight-connected neighborhoods.
This algorithm has more disadvantages than advantages: it is slow and consumes a lot of memory for the stack, so it would be much more correct to proceed to the next group of algorithms.
Edge Point List Algorithms
This algorithm is suitable only for those cases when the region to be painted can be specified as a polygon. We assume that we work with a polygon with vertices P1, P2, ..., PN, P1 and want to display it on the screen along with all internal points. For convenience, we assume that each edge of a polygon is defined by the coordinates of its ends x1, y1 and x2, y2 (with y2≥y1). We also agree that the x coordinate increases when moving from left to right, and the y coordinate when moving from top to bottom.
The overwhelming majority of algorithms for rasterizing polygons are based on the following assumption: any cutting straight line intersects the polygon boundary even number of times. This statement is false only in two cases:
- When the secant straight line contains an edge;
- When the secant line contains a vertex, and adjacent edges lie on one side of the secant line.
These two cases are fairly easy to detect, so when considering the algorithms for rasterizing polygons, we assume that the above assumption is always true.

The algorithm based on the list of edge points consists of three main steps:
At the first stage, all non-horizontal edges of the polygon are rasterized. For each value of y, a list of x-coordinates shaded during rasterization is compiled. For example, for the polygon under consideration, we obtain the following values (when moving clockwise):
At the second stage, for each value of y, the lists are ordered in ascending order. After that, the lists will look like this:
At the third stage, for each y, all the obtained segments are filled.
The advantage of this algorithm is that each pixel is processed strictly once. So It can be argued that this algorithm is suitable for devices where access to video memory takes a relatively long time.
There is a modification of this algorithm, optimized for memory consumption. In it, at each step, only those edges are processed that intersect with the current scan line.
XOR Algorithms
Line by line XOR processing
This method of rasterization of polygons is based on the properties of the logical exclusive-OR (XOR) operation.
This algorithm, like the algorithm with a list of edge points, begins with rasterization of the boundaries. After the borders are drawn, the fill is reduced to filling in each line the gaps between the two filled dots.
Imagine the image as a binary array I. We agree that I [x; y] = 1 when the pixel is shaded, and I [x; y] = 0 when the pixel is not shaded. It is easy to see that applying the operation I [x + 1, y] = I [x; y] XOR I [x + 1; y] to all pixels in a row will lead to an almost perfect result. As a result of this operation, all gaps will be painted over, but the last pixel in each gap will not be painted over. In most cases, this error is insignificant and inconspicuous, but if you want to get an accurate result, you can re-display the border after the completion of the algorithm, or use a small modification of this algorithm.
for y : = 1 to YMax do
begin
fl : = false ;
for x : = 1 to XMax do
begin
if I [ x , y ] = 1 then
fl : = not fl;
if fl then
I [ x , y ] : = 1 ;
end ;
end ;
The advantage of this algorithm is its extreme simplicity and high speed. The disadvantage is that the algorithm cannot work if there are extraneous images.
XOR Algorithm for Faces
The XOR method for faces is described by the following simple algorithm: For each edge in the polygon, the colors of all the pixels located to the right of this edge are inverted. In this case, the order of traversing the edges does not matter. The table shows the steps of this algorithm (clockwise):
The disadvantage of this algorithm is high time costs, since some pixels are processed more than once. In addition, the greater the distance from the image to the right border of the screen, the more unnecessary operations will be performed.
Algorithm XOR for edges with a partition
A modified version of the XOR algorithm for faces is free from some of the drawbacks. It is called the XOR algorithm for partitions with a partition. His idea is to invert the area not between the edge and the border of the screen, but between the edge and the special vertical lines (the so-called partition). Most often the partition is carried out so that it intersects the polygon. The steps of the algorithm are given in the table.
')
Source: https://habr.com/ru/post/116398/
All Articles