The task of finding the maximum on segments of fixed length

Formulation of the problem

Let an array A of length N be given, and a number K ≤ N be given. It is required to find a maximum (minimum, sum ...) in sub-spans of length K of this array. This is a special case of the RMQ (Range Minimum Query - Minimum on the Segment) problem, but with additional restrictions - the constant length of the search segment. In this solution, the task does not imply the possibility of changing the elements of the array. For definiteness, we will consider finding the maximum.

Advantages and disadvantages

This algorithm makes it possible to find the maximum on subframes of a fixed length beyond O (1), with preprocessing beyond O (N). In this case, the auxiliary memory requires 2 * N. But the main advantage can be considered a very simple implementation and clarity. The disadvantage is that the algorithm is not adapted to change the elements of the original array. Those. the change is possible, but this will require performing an order of O (K) actions.

Decision

Preprocessing

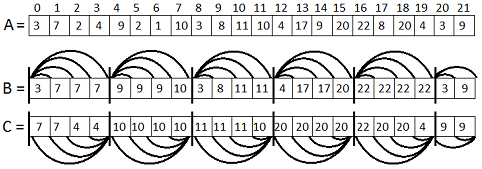
We divide the initial array A into blocks of length K-1 (why exactly K-1, you will understand just below). Then we calculate two additional arrays B and C as follows:
')
in B [i] we will store a maximum in the interval from the beginning of the current block to the i-th element;
in C [i], we will store a maximum between the i-th element and the end of the current block.

For example, in B [2] we will store a maximum from A [0] to A [2], and in C [2] - a maximum from A [2] to A [3]. It is clear that this operation can be performed in O (n). The following figure shows an example for N = 22, K = 5:

Processing request

Now, using this simple structure, you can easily find a maximum on a segment of length K. We specially made blocks of length K-1, so that the edges of any query always fall into two adjacent blocks. And, therefore, with any query, the segment will include the boundary of 2 blocks. We call it T. The left edge of the segment is l, the right edge is r. Now, in order to get the maximum, we only need to take max (C [l], B [r]). Indeed, C [l] is the maximum in the interval from l to T, and B [r] is the maximum from T to r, and, therefore, the maximum from C [l] and B [r] will be the maximum in the segment from l to r.

Implementation

Below is the simplest implementation in C ++;

vector< int > B, C; void build(const vector< int > A, int k) { int n = A.size(); B.resize(n); C.resize(n); k--; //  B for(int i = 0; i < n; i++) { if(i % k) B[i] = max(A[i], B[i - 1]); else B[i] = A[i]; } //  C C.back() = A.back(); for(int i = n - 2; i >= 0; i--) { if((i + 1) % k) C[i] = max(A[i], C[i + 1]); else C[i] = A[i]; } } int GetMax(int l, int k) { return max(C[l], B[l + k - 1]); } 

For proper operation, it is also necessary that K, supplied to the input of the build and GetMax functions, be the same.

Obviously, this implementation of the build function is not optimal, but it is the most simple and straightforward. At each next step, a new value is calculated based on the previous one. Below is a faster implementation.

 void build(const vector< int > A, int k) { int n = A.size(); B.resize(n); C.resize(n); B.front() = A.front(); C.back() = A.back(); k--; for(int i1(1), i2(n - 2); i1 < n; i1++, i2--) { B[i1] = (i1 % k) ? max(A[i1], B[i1 - 1]) : A[i1]; C[i2] = ((i2 + 1) % k) ? max(A[i2], C[i2 + 1]) : A[i2]; } } 

Total

As you can see, the algorithm is very simple both in terms of implementation and in terms of understanding. It gives the asymptotically best estimate O (1) for finding the maximum on a subsegment of a given length. This structure is easy to change to find a minimum or amount. In addition, the maximum number of possible options will be equal to NK, and therefore, using this structure, you can count all possible combinations for O (n). At each time point, only two adjacent blocks of length K need to be stored in memory, which will reduce the size of the memory in more advanced implementations.

The authorship of the algorithm belongs to Van Hercu.

Links

RMQ Task - 1. Static RMQ
RMQ Task - 2. Segment Tree
Solving the same problem by modifying the stack (e-maxx)
More about RMQ (e-maxx)
A large amount of information (in English)