MinHash - we identify similar sets
Strongly welcome! Last time I wrote about a probabilistic algorithm for determining whether an element belongs to a set, this time it will be about a probabilistic assessment of similarity. You do not need a great mind to think of the following indicator of similarity of two sets A and B:
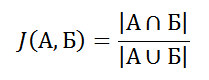
That is, the number of elements in the intersection divided by the number of elements in the union. This estimate is called the Jacquard coefficient (Jaccard, therefore “J”), the coefficient is zero when the sets have no common elements, and one when the sets are equal, otherwise the value is somewhere in the middle.
')
Let's figure out how to calculate this coefficient for a pair of string sets, let's say we have decided to find out how one piece of text is similar to another. To begin with, we need to break the text into separate words - these will be the elements of our sets, then we need to somehow calculate the dimensions of the intersection and the union.
Usually, to efficiently perform the last two operations, sets are represented as hash tables without values associated with keys, such a structure works very quickly. The construction of the table is O (n), they need two, the calculation of the intersection is O (n) and the calculation of the union is also O (n), where n is the number of words in the text. Everything seems to be fine, but let's complicate the task.
Suppose that we have a set of text data (posts, comments, etc.) stored in the database, and when adding new entries, we need to weed out too similar to existing ones. In this case, you have to load all the documents and build hash tables for them. Although this is done fairly quickly, the number of operations directly depends on the size of the documents and their number.
The latter problem can be solved by indexing, say, the same Sphinx, then for comparison, you can only download documents that have a certain subset of common words. It works well, but only for small documents, for large ones, the tested subsets become too large. We will deal with the solution of the first and this derivative problem.
Suppose we have: two sets A, B and a hash function h, which can count hashes for the elements of these sets. Next, we define the function h min (S), which computes the function h for all the members of some set S and returns its smallest value. Now, let's start to calculate h min (A) and h min (B) for different pairs of sets, the question is: what is the probability that h min (A) = h min (B)?
If you think about it, this probability should be proportional to the size of the intersection of sets - in the absence of common members, it tends to zero and to unity when the sets are equal, in intermediate cases it is somewhere in the middle. Nothing like? Yeah, that's right, this is J (A, B) - the Jacquard coefficient!
The trouble is that if we just calculate h min (A) and h min (B) for our two text fragments, and then compare the values, it will not give us anything, because There are only two options - equal or not equal. We need to somehow get a sufficient amount of statistics on our sets to calculate the closest to truth J (A, B). This is done simply, instead of one function h, we introduce several independent hash functions, or rather k functions:

, where ε is the desired largest error value. So, to calculate J (A, B) with an error of no more than 0.1, 100 hash functions are necessary — not small. What are the advantages?
First, we can calculate the so-called signature H min (S), i.e. the minima of all hash functions for the set S. The complexity of its calculations is more than when building a hash table, but, nevertheless, it is linear, and you need to do this for each document only once, for example when adding to the database, then it’s enough to operate signature only.
Secondly, as you may have noticed, the signature has a fixed size for a given maximum error value. In order to compare any two sets of any size, you must perform a fixed number of operations. In addition, in theory, signatures are much more convenient to index. “In theory,” because their indexing does not fit well with relational databases, full-text engines are also not much. At least I couldn’t figure out how to make it beautiful.
As usual, we need a family of hash functions:
MinHash itself:
Example of use:
In reality, the accuracy will be slightly lower, since real hash functions are not perfect. You can put up with it or introduce a couple of additional functions, although a couple or the other will not help much.
For some reason it is not mentioned anywhere, what should be the number of bits produced by functions. In theory, this number should be such that all possible input values are presented. For example, in English about 250,000 words, therefore, about 18 bits is enough. But it is better, again, to err and add a couple of extra bits.
Indexing signatures is beneficial not for all their component values, but for a small subset. This reduces the size of the indices and speeds up the sample, but is fraught with danger — a hash function that may have at least some frequently used word (prepositions, articles, etc.) may be caught, and the index selectivity will not be the best. In addition, it increases the likelihood of error. Still, this is a bad idea.
You can align the texts here . Thank you for your attention, see you soon.
PS HabraStoraj all give an error when loading pictures or just me?
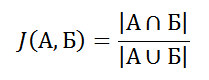
That is, the number of elements in the intersection divided by the number of elements in the union. This estimate is called the Jacquard coefficient (Jaccard, therefore “J”), the coefficient is zero when the sets have no common elements, and one when the sets are equal, otherwise the value is somewhere in the middle.
')
How to count it?
Let's figure out how to calculate this coefficient for a pair of string sets, let's say we have decided to find out how one piece of text is similar to another. To begin with, we need to break the text into separate words - these will be the elements of our sets, then we need to somehow calculate the dimensions of the intersection and the union.
Usually, to efficiently perform the last two operations, sets are represented as hash tables without values associated with keys, such a structure works very quickly. The construction of the table is O (n), they need two, the calculation of the intersection is O (n) and the calculation of the union is also O (n), where n is the number of words in the text. Everything seems to be fine, but let's complicate the task.
Suppose that we have a set of text data (posts, comments, etc.) stored in the database, and when adding new entries, we need to weed out too similar to existing ones. In this case, you have to load all the documents and build hash tables for them. Although this is done fairly quickly, the number of operations directly depends on the size of the documents and their number.
The latter problem can be solved by indexing, say, the same Sphinx, then for comparison, you can only download documents that have a certain subset of common words. It works well, but only for small documents, for large ones, the tested subsets become too large. We will deal with the solution of the first and this derivative problem.
MinHash key idea
Suppose we have: two sets A, B and a hash function h, which can count hashes for the elements of these sets. Next, we define the function h min (S), which computes the function h for all the members of some set S and returns its smallest value. Now, let's start to calculate h min (A) and h min (B) for different pairs of sets, the question is: what is the probability that h min (A) = h min (B)?
If you think about it, this probability should be proportional to the size of the intersection of sets - in the absence of common members, it tends to zero and to unity when the sets are equal, in intermediate cases it is somewhere in the middle. Nothing like? Yeah, that's right, this is J (A, B) - the Jacquard coefficient!
The trouble is that if we just calculate h min (A) and h min (B) for our two text fragments, and then compare the values, it will not give us anything, because There are only two options - equal or not equal. We need to somehow get a sufficient amount of statistics on our sets to calculate the closest to truth J (A, B). This is done simply, instead of one function h, we introduce several independent hash functions, or rather k functions:

, where ε is the desired largest error value. So, to calculate J (A, B) with an error of no more than 0.1, 100 hash functions are necessary — not small. What are the advantages?
First, we can calculate the so-called signature H min (S), i.e. the minima of all hash functions for the set S. The complexity of its calculations is more than when building a hash table, but, nevertheless, it is linear, and you need to do this for each document only once, for example when adding to the database, then it’s enough to operate signature only.
Secondly, as you may have noticed, the signature has a fixed size for a given maximum error value. In order to compare any two sets of any size, you must perform a fixed number of operations. In addition, in theory, signatures are much more convenient to index. “In theory,” because their indexing does not fit well with relational databases, full-text engines are also not much. At least I couldn’t figure out how to make it beautiful.
Toy implementation
As usual, we need a family of hash functions:
function Hash(size) { var seed = Math.floor(Math.random() * size) + 32; return function (string) { var result = 1; for (var i = 0; i < string.length; ++i) result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF; return result; }; } MinHash itself:
function MinHash(max_error) { var function_count = Math.round(1 / (max_error * max_error)); var functions = []; for (var i = 0; i < function_count; ++i) functions[i] = Hash(function_count); function find_min(set, function_) { var min = 0xFFFFFFFF; for (var i = 0; i < set.length; ++i) { var hash = function_(set[i]); if (hash < min) min = hash; } return min; } function signature(set) { var result = []; for (var i = 0; i < function_count; ++i) result[i] = find_min(set, functions[i]); return result; } function similarity(sig_a, sig_b) { var equal_count = 0; for (var i = 0; i < function_count; ++i) if (sig_a[i] == sig_b[i]) ++equal_count; return equal_count / function_count; } return {signature: signature, similarity: similarity}; } Example of use:
var set_a = ['apple', 'orange']; var set_b = ['apple', 'peach']; var min_hash = MinHash(0.05); var sig_a = min_hash.signature(set_a); var sig_b = min_hash.signature(set_b); alert(min_hash.similarity(sig_a, sig_b)); Subtle moments
In reality, the accuracy will be slightly lower, since real hash functions are not perfect. You can put up with it or introduce a couple of additional functions, although a couple or the other will not help much.
For some reason it is not mentioned anywhere, what should be the number of bits produced by functions. In theory, this number should be such that all possible input values are presented. For example, in English about 250,000 words, therefore, about 18 bits is enough. But it is better, again, to err and add a couple of extra bits.
You can align the texts here . Thank you for your attention, see you soon.
PS HabraStoraj all give an error when loading pictures or just me?
Source: https://habr.com/ru/post/115147/
All Articles