How to make from 123456789 the number 100 or 0
At the end of the first chapter, I found an example of the following “Arithmetic curiosities” in “Entertaining arithmetic” of the famous popularizer of sciences Yakov Isidorovich Perelman:
100 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 * 9
100 = 12 + 3-4 + 5 + 67 + 8 + 9
100 = 12-3-4 + 5-6 + 7 + 89
100 = 123 + 4-5 + 67-89
100 = 123-45-67 + 89
The first of these solutions I found in elementary school at the Mathematics Olympiad, and now thinking that maybe this victory affected my future development, I decided to pay tribute to this task and find all possible solutions by writing the appropriate Python script.
Let the task be set as follows: there is a string of numbers 123456789 (even if I really am not very interested in zero), between which you can put 4 arithmetic operations (+, -, *, /) anywhere or not put anything (that is, put an empty string, then two- and more-digit numbers are formed) so that the total expression will result in 100, as in the examples in the book above. Nothing else is possible, no brackets, no permutations, no duplicates, no throwings.
')
I did not learn programming, and realized the task as I came up with. Therefore, I have a question: “How could this be done better?” .
And I came up with this: in order to sort through all the possible inserts of space characters (there are five of them: either an empty string or +, -, *, /), I presented them as options for the number in base 5, padded with zeros on the left. The length of such a number is eight characters, since there are nine digits, and then there are eight spaces between them. The zeros correspond to empty strings, all others to arithmetic operations. Here's what happened:
For 100 there were 101 such solutions, and some of them are quite funny, especially with fractions:
123 + 45-67 + 8-9 = 100
123 + 4-5 + 67-89 = 100
123 + 4 * 5-6 * 7 + 8-9 = 100
123-45-67 + 89 = 100
123-4-5-6-7 + 8-9 = 100
12 + 34 + 5 * 6 + 7 + 8 + 9 = 100
12 + 34-5 + 6 * 7 + 8 + 9 = 100
12 + 34-5-6 + 7 * 8 + 9 = 100
12 + 34-5-6-7 + 8 * 9 = 100
12 + 3 + 4 + 5-6-7 + 89 = 100
12 + 3 + 4-56 / 7 + 89 = 100
12 + 3-4 + 5 + 67 + 8 + 9 = 100
12 + 3 * 45 + 6 * 7-89 = 100
12 + 3 * 4 + 5 + 6 + 7 * 8 + 9 = 100
12 + 3 * 4 + 5 + 6-7 + 8 * 9 = 100
12 + 3 * 4-5-6 + 78 + 9 = 100
12-3 + 4 * 5 + 6 + 7 * 8 + 9 = 100
12-3 + 4 * 5 + 6-7 + 8 * 9 = 100
12-3-4 + 5-6 + 7 + 89 = 100
12-3-4 + 5 * 6 + 7 * 8 + 9 = 100
12-3-4 + 5 * 6-7 + 8 * 9 = 100
12 * 3-4 + 5-6 + 78-9 = 100
12 * 3-4-5-6 + 7 + 8 * 9 = 100
12 * 3-4 * 5 + 67 + 8 + 9 = 100
12/3 + 4 * 5-6-7 + 89 = 100
12/3 + 4 * 5 * 6-7-8-9 = 100
12/3 + 4 * 5 * 6 * 7 / 8-9 = 100
12/3/4 + 5 * 6 + 78-9 = 100
1 + 234-56-7-8 * 9 = 100
1 + 234 * 5 * 6/78 + 9 = 100
1 + 234 * 5 / 6-7-89 = 100
1 + 23-4 + 56 + 7 + 8 + 9 = 100
1 + 23-4 + 56/7 + 8 * 9 = 100
1 + 23-4 + 5 + 6 + 78-9 = 100
1 + 23-4-5 + 6 + 7 + 8 * 9 = 100
1 + 23 * 4 + 56/7 + 8-9 = 100
1 + 23 * 4 + 5-6 + 7-8 + 9 = 100
1 + 23 * 4-5 + 6 + 7 + 8-9 = 100
1 + 2 + 34-5 + 67-8 + 9 = 100
1 + 2 + 34 * 5 + 6-7-8 * 9 = 100
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 * 9 = 100
1 + 2 + 3-45 + 67 + 8 * 9 = 100
1 + 2 + 3-4 + 5 + 6 + 78 + 9 = 100
1 + 2 + 3-4 * 5 + 6 * 7 + 8 * 9 = 100
1 + 2 + 3 * 4-5-6 + 7 + 89 = 100
1 + 2 + 3 * 4 * 56 / 7-8 + 9 = 100
1 + 2 + 3 * 4 * 5/6 + 78 + 9 = 100
1 + 2-3 * 4 + 5 * 6 + 7 + 8 * 9 = 100
1 + 2-3 * 4-5 + 6 * 7 + 8 * 9 = 100
1 + 2 * 34-56 + 78 + 9 = 100
1 + 2 * 3 + 4 + 5 + 67 + 8 + 9 = 100
1 + 2 * 3 + 4 * 5-6 + 7 + 8 * 9 = 100
1 + 2 * 3-4 + 56/7 + 89 = 100
1 + 2 * 3-4-5 + 6 + 7 + 89 = 100
1 + 2 * 3 * 4 * 5/6 + 7 + 8 * 9 = 100
1-23 + 4 * 5 + 6 + 7 + 89 = 100
1-23-4 + 5 * 6 + 7 + 89 = 100
1-23-4-5 + 6 * 7 + 89 = 100
1-2 + 3 + 45 + 6 + 7 * 8-9 = 100
1-2 + 3 * 4 + 5 + 67 + 8 + 9 = 100
1-2 + 3 * 4 * 5 + 6 * 7 + 8-9 = 100
1-2 + 3 * 4 * 5-6 + 7 * 8-9 = 100
1-2-34 + 56 + 7 + 8 * 9 = 100
1-2-3 + 45 + 6 * 7 + 8 + 9 = 100
1-2-3 + 45-6 + 7 * 8 + 9 = 100
1-2-3 + 45-6-7 + 8 * 9 = 100
1-2-3 + 4 * 56/7 + 8 * 9 = 100
1-2-3 + 4 * 5 + 67 + 8 + 9 = 100
1-2 * 3 + 4 * 5 + 6 + 7 + 8 * 9 = 100
1-2 * 3-4 + 5 * 6 + 7 + 8 * 9 = 100
1-2 * 3-4-5 + 6 * 7 + 8 * 9 = 100
1 * 234 + 5-67-8 * 9 = 100
1 * 23 + 4 + 56/7 * 8 + 9 = 100
1 * 23 + 4 + 5 + 67-8 + 9 = 100
1 * 23-4 + 5-6-7 + 89 = 100
1 * 23-4-56 / 7 + 89 = 100
1 * 23 * 4-56 / 7/8 + 9 = 100
1 * 2 + 34 + 56 + 7-8 + 9 = 100
1 * 2 + 34 + 5 + 6 * 7 + 8 + 9 = 100
1 * 2 + 34 + 5-6 + 7 * 8 + 9 = 100
1 * 2 + 34 + 5-6-7 + 8 * 9 = 100
1 * 2 + 34-56 / 7 + 8 * 9 = 100
1 * 2 + 3 + 45 + 67-8-9 = 100
1 * 2 + 3 + 4 * 5 + 6 + 78-9 = 100
1 * 2 + 3-4 + 5 * 6 + 78-9 = 100
1 * 2 + 3 * 4 + 5-6 + 78 + 9 = 100
1 * 2-3 + 4 + 56/7 + 89 = 100
1 * 2-3 + 4-5 + 6 + 7 + 89 = 100
1 * 2-3 + 4 * 5-6 + 78 + 9 = 100
1 * 2 * 34 + 56-7-8-9 = 100
1 * 2 * 3 + 4 + 5 + 6 + 7 + 8 * 9 = 100
1 * 2 * 3-45 + 67 + 8 * 9 = 100
1 * 2 * 3-4 + 5 + 6 + 78 + 9 = 100
1 * 2 * 3-4 * 5 + 6 * 7 + 8 * 9 = 100
1 * 2 * 3 * 4 + 5 + 6 + 7 * 8 + 9 = 100
1 * 2 * 3 * 4 + 5 + 6-7 + 8 * 9 = 100
1 * 2 * 3 * 4-5-6 + 78 + 9 = 100
1 * 2/3 + 4 * 5/6 + 7 + 89 = 100
1/2 * 34-5 + 6-7 + 89 = 100
1/2 * 3/4 * 56 + 7 + 8 * 9 = 100
1/2/3 * 456 + 7 + 8 + 9 = 100
Then I decided to view the complete dependence of the number of possible solutions of such expansions on all possible sums, including non-integer ones. For this, the loop has become a function that works to fill the dictionary:
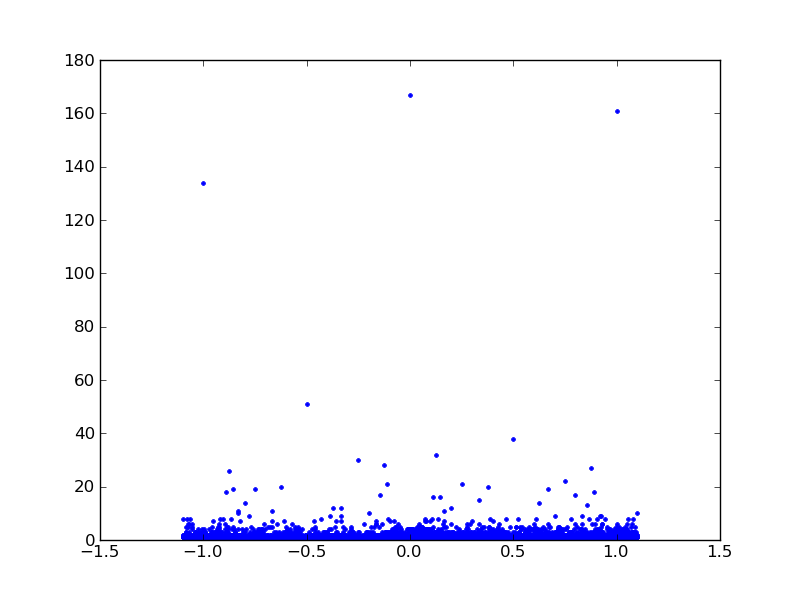
Dependency lists ylist = f (xlist) are drawn using matplotlib. Dependency has a peak at zero with 167 solutions:
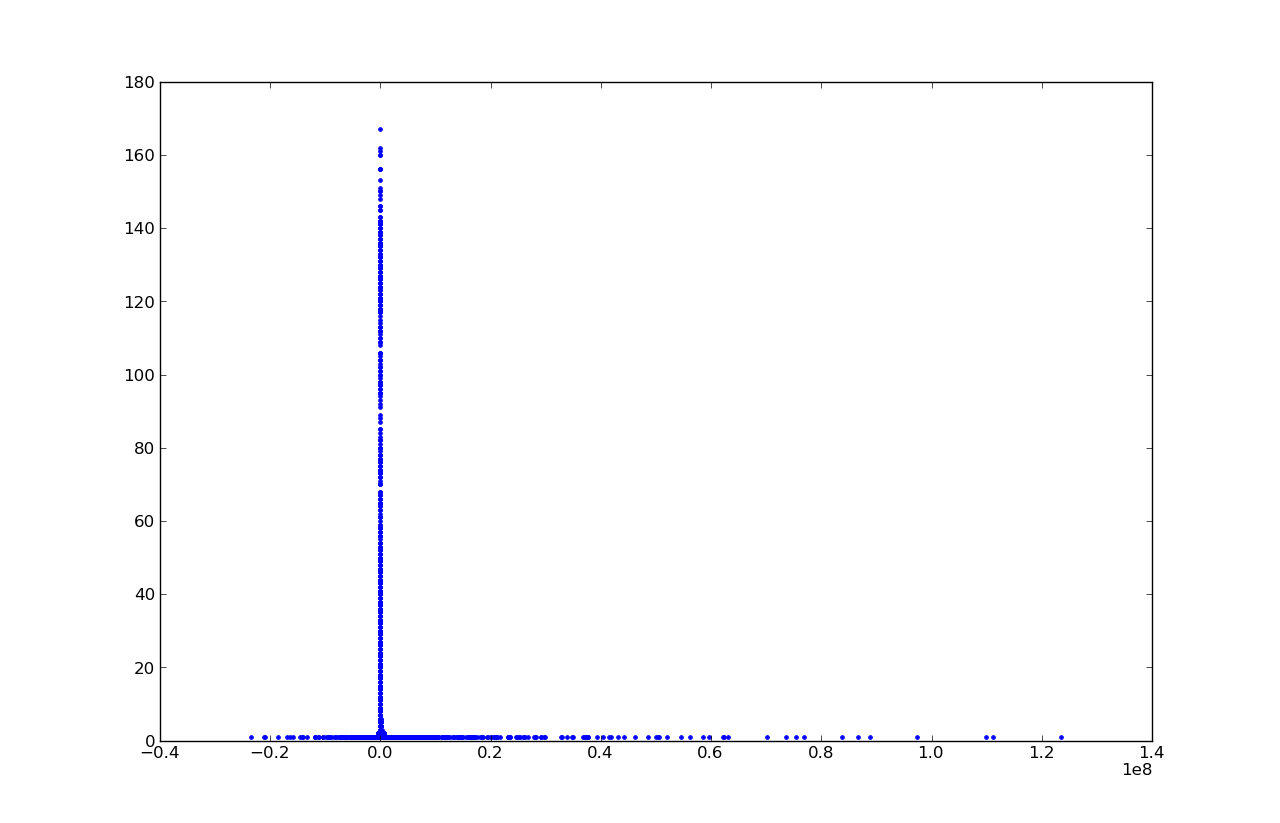
The left branch is not symmetrical to the right, because we can’t put a minus before the option 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9. The closer to zero, the more often there are real numbers that can be represented in several possible ways.
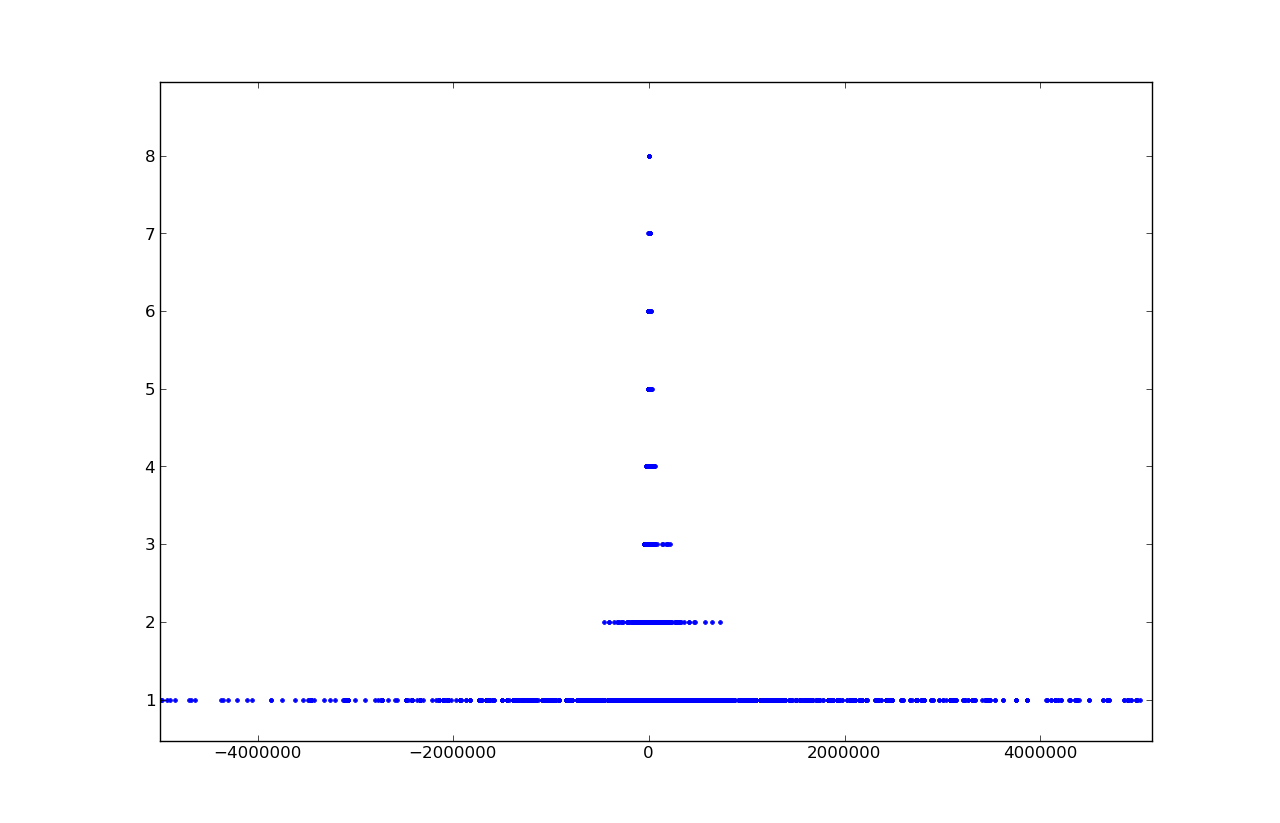
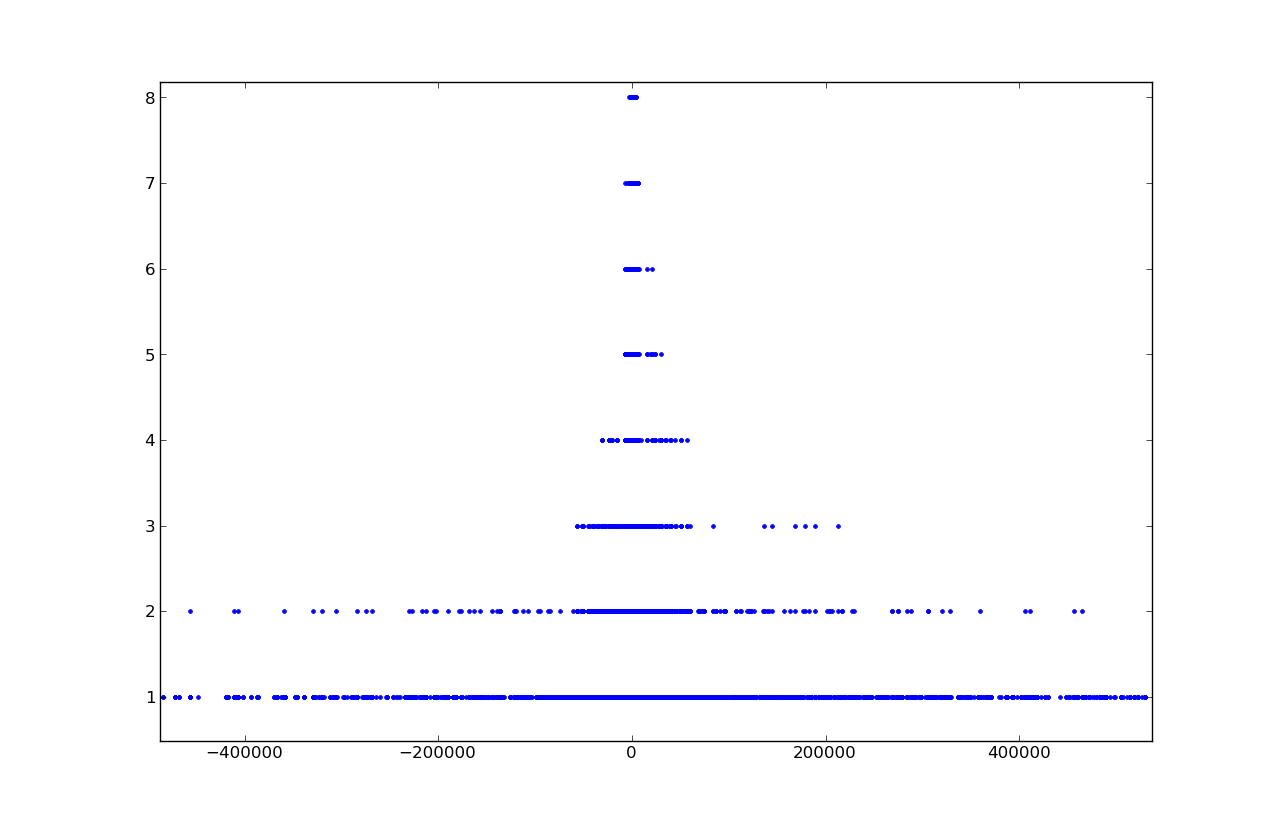
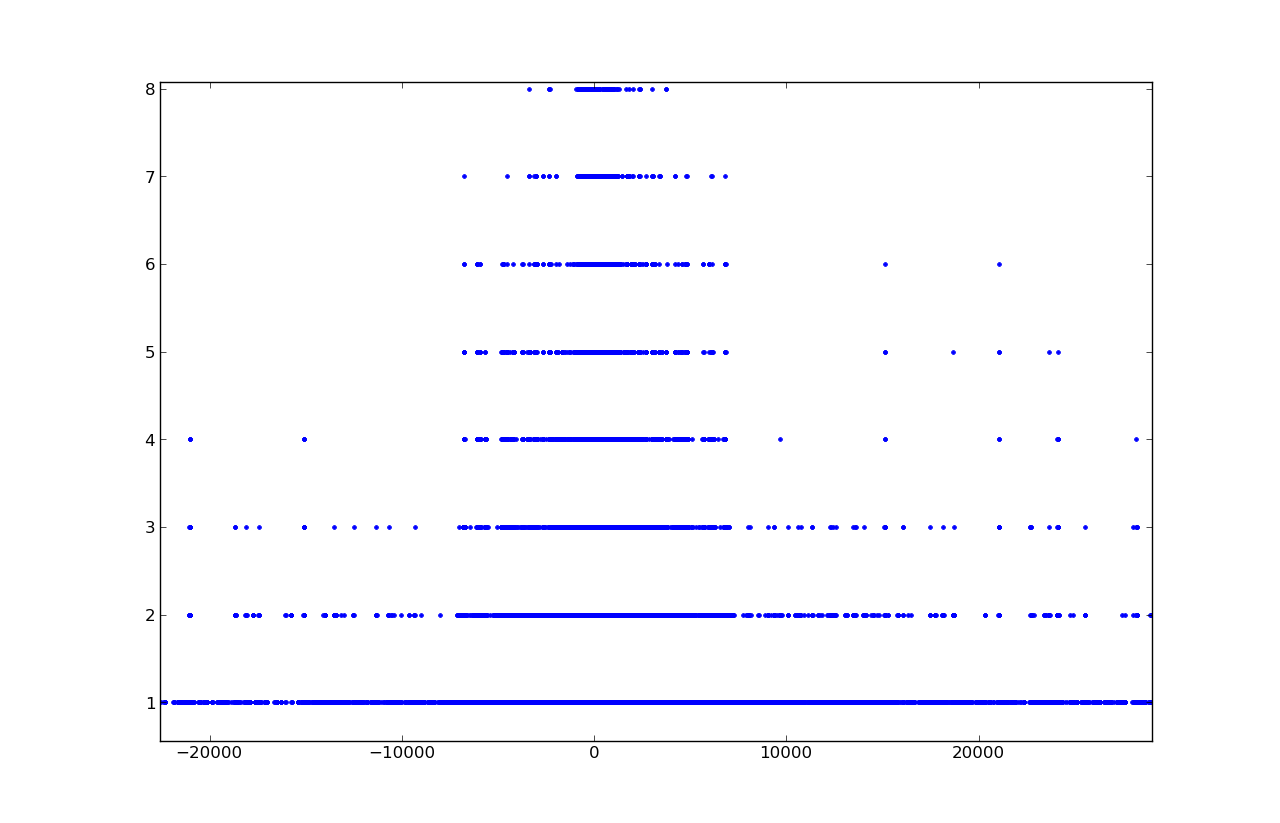
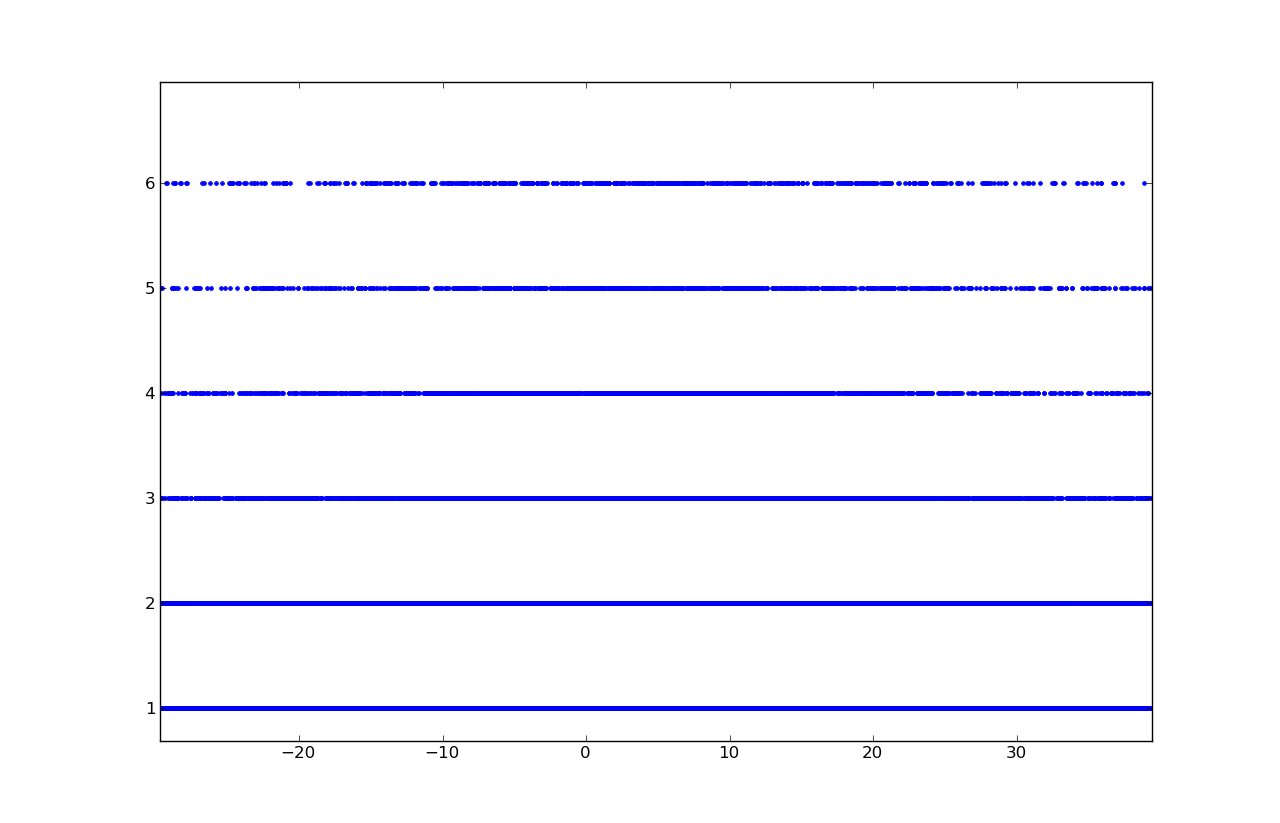
Separate consideration for solutions in the area [-1.1, 1.1]: the greatest number of solutions falls on zero, then on the integers -1, 1, then on half-integer -0.5, 0.5.
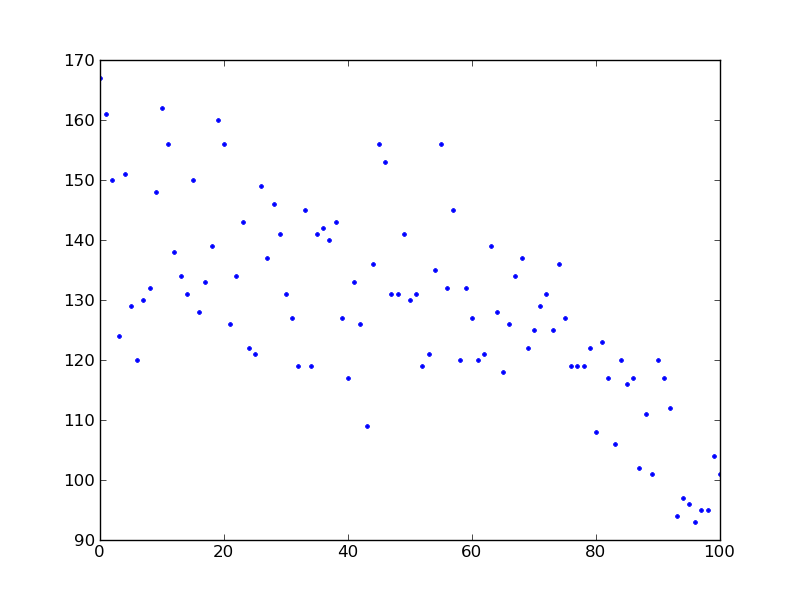
It is verified that any of the integers from 0 to 100 can be expressed in this way:
Maybe this task will be pleasant and just to ask someone, such as your own child or friend, for the counting speed and ability to handle numbers, as I once was in elementary school and I needed to find one solution, though as I see now, there were a lot more of them. And you can try yourself in your mind or on paper to find at least one of the 167 solutions for zero.
UPD: Do not think that all these charts are something serious. There is nothing serious here, except for the formulation of the problem, the code and the proposal for the pythonists to try to write something faster.
UPD2: A great option for improving the code was written in the comments hellman
100 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 * 9
100 = 12 + 3-4 + 5 + 67 + 8 + 9
100 = 12-3-4 + 5-6 + 7 + 89
100 = 123 + 4-5 + 67-89
100 = 123-45-67 + 89
The first of these solutions I found in elementary school at the Mathematics Olympiad, and now thinking that maybe this victory affected my future development, I decided to pay tribute to this task and find all possible solutions by writing the appropriate Python script.
Let the task be set as follows: there is a string of numbers 123456789 (even if I really am not very interested in zero), between which you can put 4 arithmetic operations (+, -, *, /) anywhere or not put anything (that is, put an empty string, then two- and more-digit numbers are formed) so that the total expression will result in 100, as in the examples in the book above. Nothing else is possible, no brackets, no permutations, no duplicates, no throwings.
')
I did not learn programming, and realized the task as I came up with. Therefore, I have a question: “How could this be done better?” .
And I came up with this: in order to sort through all the possible inserts of space characters (there are five of them: either an empty string or +, -, *, /), I presented them as options for the number in base 5, padded with zeros on the left. The length of such a number is eight characters, since there are nine digits, and then there are eight spaces between them. The zeros correspond to empty strings, all others to arithmetic operations. Here's what happened:
Copy Source | Copy HTML<br/> from __future__ import division # for 2.x version <br/> <br/>s = '123456789' <br/>d = { '0' : '' , '1' : '+' , '2' : '-' , '3' : '*' , '4' : '/' }<br/>sum_num = 100 <br/>count = 0 <br/> <br/> def to_new_base (n, new_base):<br/> s = []<br/> if n == 0 :<br/> s.append( '0' )<br/> while n:<br/> s.append( str (n % new_base))<br/> n = n // new_base<br/> num = '{0:0>8}' .format( '' .join(s[::- 1 ]))<br/> return num<br/> <br/> <br/> for n in xrange ( int ( '44444444' , 5 )):<br/> num = to_new_base (n, 5 )<br/> expr = '' <br/> for i, j in zip (s, num):<br/> expr += i + d[j]<br/> expr += '9' <br/> if eval (expr) == sum_num:<br/> print ( '{0} = {1}' .format(expr, sum_num))<br/> count += 1 <br/> <br/> <br/> print 'So, {0} expressions for {1}' .format(count, sum_num) <br/>For 100 there were 101 such solutions, and some of them are quite funny, especially with fractions:
123 + 45-67 + 8-9 = 100
123 + 4-5 + 67-89 = 100
123 + 4 * 5-6 * 7 + 8-9 = 100
123-45-67 + 89 = 100
123-4-5-6-7 + 8-9 = 100
12 + 34 + 5 * 6 + 7 + 8 + 9 = 100
12 + 34-5 + 6 * 7 + 8 + 9 = 100
12 + 34-5-6 + 7 * 8 + 9 = 100
12 + 34-5-6-7 + 8 * 9 = 100
12 + 3 + 4 + 5-6-7 + 89 = 100
12 + 3 + 4-56 / 7 + 89 = 100
12 + 3-4 + 5 + 67 + 8 + 9 = 100
12 + 3 * 45 + 6 * 7-89 = 100
12 + 3 * 4 + 5 + 6 + 7 * 8 + 9 = 100
12 + 3 * 4 + 5 + 6-7 + 8 * 9 = 100
12 + 3 * 4-5-6 + 78 + 9 = 100
12-3 + 4 * 5 + 6 + 7 * 8 + 9 = 100
12-3 + 4 * 5 + 6-7 + 8 * 9 = 100
12-3-4 + 5-6 + 7 + 89 = 100
12-3-4 + 5 * 6 + 7 * 8 + 9 = 100
12-3-4 + 5 * 6-7 + 8 * 9 = 100
12 * 3-4 + 5-6 + 78-9 = 100
12 * 3-4-5-6 + 7 + 8 * 9 = 100
12 * 3-4 * 5 + 67 + 8 + 9 = 100
12/3 + 4 * 5-6-7 + 89 = 100
12/3 + 4 * 5 * 6-7-8-9 = 100
12/3 + 4 * 5 * 6 * 7 / 8-9 = 100
12/3/4 + 5 * 6 + 78-9 = 100
1 + 234-56-7-8 * 9 = 100
1 + 234 * 5 * 6/78 + 9 = 100
1 + 234 * 5 / 6-7-89 = 100
1 + 23-4 + 56 + 7 + 8 + 9 = 100
1 + 23-4 + 56/7 + 8 * 9 = 100
1 + 23-4 + 5 + 6 + 78-9 = 100
1 + 23-4-5 + 6 + 7 + 8 * 9 = 100
1 + 23 * 4 + 56/7 + 8-9 = 100
1 + 23 * 4 + 5-6 + 7-8 + 9 = 100
1 + 23 * 4-5 + 6 + 7 + 8-9 = 100
1 + 2 + 34-5 + 67-8 + 9 = 100
1 + 2 + 34 * 5 + 6-7-8 * 9 = 100
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 * 9 = 100
1 + 2 + 3-45 + 67 + 8 * 9 = 100
1 + 2 + 3-4 + 5 + 6 + 78 + 9 = 100
1 + 2 + 3-4 * 5 + 6 * 7 + 8 * 9 = 100
1 + 2 + 3 * 4-5-6 + 7 + 89 = 100
1 + 2 + 3 * 4 * 56 / 7-8 + 9 = 100
1 + 2 + 3 * 4 * 5/6 + 78 + 9 = 100
1 + 2-3 * 4 + 5 * 6 + 7 + 8 * 9 = 100
1 + 2-3 * 4-5 + 6 * 7 + 8 * 9 = 100
1 + 2 * 34-56 + 78 + 9 = 100
1 + 2 * 3 + 4 + 5 + 67 + 8 + 9 = 100
1 + 2 * 3 + 4 * 5-6 + 7 + 8 * 9 = 100
1 + 2 * 3-4 + 56/7 + 89 = 100
1 + 2 * 3-4-5 + 6 + 7 + 89 = 100
1 + 2 * 3 * 4 * 5/6 + 7 + 8 * 9 = 100
1-23 + 4 * 5 + 6 + 7 + 89 = 100
1-23-4 + 5 * 6 + 7 + 89 = 100
1-23-4-5 + 6 * 7 + 89 = 100
1-2 + 3 + 45 + 6 + 7 * 8-9 = 100
1-2 + 3 * 4 + 5 + 67 + 8 + 9 = 100
1-2 + 3 * 4 * 5 + 6 * 7 + 8-9 = 100
1-2 + 3 * 4 * 5-6 + 7 * 8-9 = 100
1-2-34 + 56 + 7 + 8 * 9 = 100
1-2-3 + 45 + 6 * 7 + 8 + 9 = 100
1-2-3 + 45-6 + 7 * 8 + 9 = 100
1-2-3 + 45-6-7 + 8 * 9 = 100
1-2-3 + 4 * 56/7 + 8 * 9 = 100
1-2-3 + 4 * 5 + 67 + 8 + 9 = 100
1-2 * 3 + 4 * 5 + 6 + 7 + 8 * 9 = 100
1-2 * 3-4 + 5 * 6 + 7 + 8 * 9 = 100
1-2 * 3-4-5 + 6 * 7 + 8 * 9 = 100
1 * 234 + 5-67-8 * 9 = 100
1 * 23 + 4 + 56/7 * 8 + 9 = 100
1 * 23 + 4 + 5 + 67-8 + 9 = 100
1 * 23-4 + 5-6-7 + 89 = 100
1 * 23-4-56 / 7 + 89 = 100
1 * 23 * 4-56 / 7/8 + 9 = 100
1 * 2 + 34 + 56 + 7-8 + 9 = 100
1 * 2 + 34 + 5 + 6 * 7 + 8 + 9 = 100
1 * 2 + 34 + 5-6 + 7 * 8 + 9 = 100
1 * 2 + 34 + 5-6-7 + 8 * 9 = 100
1 * 2 + 34-56 / 7 + 8 * 9 = 100
1 * 2 + 3 + 45 + 67-8-9 = 100
1 * 2 + 3 + 4 * 5 + 6 + 78-9 = 100
1 * 2 + 3-4 + 5 * 6 + 78-9 = 100
1 * 2 + 3 * 4 + 5-6 + 78 + 9 = 100
1 * 2-3 + 4 + 56/7 + 89 = 100
1 * 2-3 + 4-5 + 6 + 7 + 89 = 100
1 * 2-3 + 4 * 5-6 + 78 + 9 = 100
1 * 2 * 34 + 56-7-8-9 = 100
1 * 2 * 3 + 4 + 5 + 6 + 7 + 8 * 9 = 100
1 * 2 * 3-45 + 67 + 8 * 9 = 100
1 * 2 * 3-4 + 5 + 6 + 78 + 9 = 100
1 * 2 * 3-4 * 5 + 6 * 7 + 8 * 9 = 100
1 * 2 * 3 * 4 + 5 + 6 + 7 * 8 + 9 = 100
1 * 2 * 3 * 4 + 5 + 6-7 + 8 * 9 = 100
1 * 2 * 3 * 4-5-6 + 78 + 9 = 100
1 * 2/3 + 4 * 5/6 + 7 + 89 = 100
1/2 * 34-5 + 6-7 + 89 = 100
1/2 * 3/4 * 56 + 7 + 8 * 9 = 100
1/2/3 * 456 + 7 + 8 + 9 = 100
Then I decided to view the complete dependence of the number of possible solutions of such expansions on all possible sums, including non-integer ones. For this, the loop has become a function that works to fill the dictionary:
Copy Source | Copy HTML<br/>figure = {}<br/>xlist = []<br/>ylist = []<br/> <br/> def func ():<br/> for n in range ( int ( '44444444' , 5 )):<br/> num = to_new_base(n, 5 )<br/> expr = '' <br/> for i, j in zip (line, num):<br/> expr += i + d[j]<br/> expr += '9' <br/> num_sum = eval (expr)<br/> if num_sum in figure:<br/> figure[num_sum] += 1 <br/> else :<br/> figure[num_sum] = 1 <br/> <br/> for key in sorted (figure):<br/> xlist.append(key)<br/> ylist.append(figure[key]) <br/>Dependency lists ylist = f (xlist) are drawn using matplotlib. Dependency has a peak at zero with 167 solutions:

The left branch is not symmetrical to the right, because we can’t put a minus before the option 1 * 2 * 3 * 4 * 5 * 6 * 7 * 8 * 9. The closer to zero, the more often there are real numbers that can be represented in several possible ways.




Separate consideration for solutions in the area [-1.1, 1.1]: the greatest number of solutions falls on zero, then on the integers -1, 1, then on half-integer -0.5, 0.5.

It is verified that any of the integers from 0 to 100 can be expressed in this way:

Maybe this task will be pleasant and just to ask someone, such as your own child or friend, for the counting speed and ability to handle numbers, as I once was in elementary school and I needed to find one solution, though as I see now, there were a lot more of them. And you can try yourself in your mind or on paper to find at least one of the 167 solutions for zero.
UPD: Do not think that all these charts are something serious. There is nothing serious here, except for the formulation of the problem, the code and the proposal for the pythonists to try to write something faster.
UPD2: A great option for improving the code was written in the comments hellman
Source: https://habr.com/ru/post/115066/
All Articles