Fuzzy search in text and dictionary

Introduction

Fuzzy search algorithms (also known as similarity or fuzzy string search ) are the basis of spell check systems and full-fledged search engines like Google or Yandex. For example, such algorithms are used for functions like “Perhaps you meant ...” in the same search engines.

In this review article I will consider the following concepts, methods and algorithms:

• Levenshtein distance
• Distance Damerau-Levenshteyn
• Bitap algorithm with modifications from Wu and Manber
• Sample extension algorithm
• N-gram method
• Signature hashing
• BK-trees

And also I will conduct a comparative testing of the quality and performance of the algorithms.

So...

Fuzzy search is an extremely useful feature of any search engine. At the same time, its effective implementation is much more complicated than the implementation of a simple search by exact coincidence.

The task of a fuzzy search can be formulated as follows:
"For a given word, find in the text or a dictionary of size n all words that match this word (or begin with this word), taking into account k possible differences."
')
For example, when requesting "Machine" with two possible errors, find the words "Machine", "Machina", "Malina", "Kalina" and so on.

Fuzzy search algorithms are characterized by a metric - a function of the distance between two words, which allows to evaluate the degree of their similarity in a given context. A rigorous mathematical definition of a metric includes the need to meet the triangle inequality condition (X is a set of words, p is a metric):



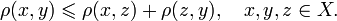
Meanwhile, in most cases, the metric implies a more general concept that does not require the fulfillment of such a condition; this concept can also be called distance .

Among the most well-known metrics are Hamming , Levenshtein and Damerau-Levenshtein distances . Moreover, the Hamming distance is a metric only on a set of words of the same length, which severely limits its scope.

However, in practice, the Hamming distance turns out to be practically useless, yielding to the more natural from the point of view of man metrics, which will be discussed below.

Levenshtein distance

The most commonly used metric is the Levenshtein distance, or the editing distance, whose calculation algorithms can be found at every step.
Nevertheless, it is worth making a few remarks regarding the most popular calculation algorithm - the Wagner-Fisher method .
The original version of this algorithm has the time complexity O (mn) and consumes O (mn) memory, where m and n are the lengths of the compared strings. The whole process can be represented by the following matrix:



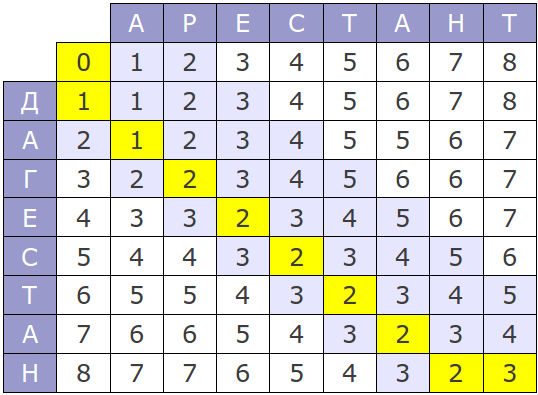
If you look at the process of the algorithm, it is easy to notice that at each step only the last two rows of the matrix are used, therefore, memory consumption can be reduced to O (min (m, n)) .



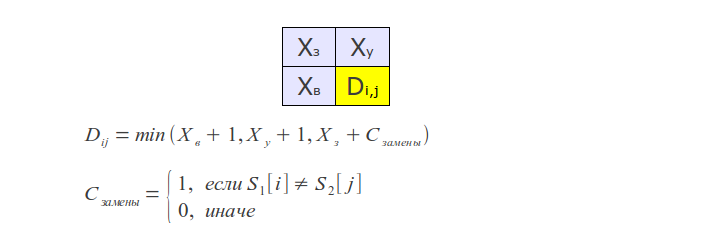
But that's not all - you can further optimize the algorithm if the task is to find no more than k differences. In this case, it is necessary to calculate in the matrix only a diagonal strip of width 2k + 1 (Ukkonen cut-off), which reduces the time complexity to O (k min (m, n)) .

Prefix distance

It is also necessary to calculate the distance between the sample prefix and the string — that is, to find the distance between the given prefix and the nearest prefix of the string. In this case, you need to take the smallest of the distances from the prefix of the sample to all the prefixes of the string. Obviously, the prefix distance cannot be considered a metric in a strict mathematical sense, which limits its use.

Often with a fuzzy search, it is not so much the value of the distance itself that is important as the fact whether it exceeds a certain value.

Distance Damerau-Levenshteyn

This variation adds another rule to the definition of the Levenshtein distance: the transposition (permutation) of two adjacent letters is also taken into account as one operation, along with inserts, deletions and replacements.
Just a couple of years ago, Frederic Damerau could guarantee that most typing errors are transpositions. Therefore, it is this metric that gives the best results in practice.



To calculate such a distance, it is enough to slightly modify the algorithm for finding the usual Levenshtein distance as follows: store not the two, but the last three rows of the matrix, and add an appropriate additional condition — if a transposition is detected, when calculating the distance, also take its cost into account.

In addition to those discussed above, there are many other distances that are sometimes used in practice, such as the Jaro-Winkler metric , many of which are available in the SimMetrics and SecondString libraries .

Fuzzy search algorithms without indexing (Online)

These algorithms are designed to search in a previously unknown text, and can be used, for example, in text editors, programs for viewing documents or web browsers to search the page. They do not require preprocessing of the text and can work with a continuous stream of data.

Linear search

Simple sequential application of a given metric (for example, Levenshtein metric) to words from the input text. When using a metric with a constraint, this method allows you to achieve optimal performance. But, at the same time, the larger the k , the stronger the running time. The asymptotic estimate of time is O (kn) .

Bitap (also known as Shift-Or or Baeza-Yates-Gonnet, and its modification from Wu-Manber)

The Bitap algorithm and its various modifications are most often used for fuzzy search without indexing. Its variation is used, for example, in agix unix-utility, which performs functions similar to standard grep , but with the support of errors in the search query and even providing limited opportunities for the use of regular expressions.

For the first time the idea of ​​this algorithm was proposed by the citizens of Ricardo Baeza-Yates and Gaston Gonnet , having published the corresponding article in 1992.
The original version of the algorithm deals only with symbol substitutions, and, in fact, calculates the Hamming distance. But a little later, Sun Wu and Udi Manber proposed a modification of this algorithm to calculate the Levenshtein distance , i.e. introduced support for inserts and deletions, and developed on its basis the first version of the agrep utility.

Bitshift operation



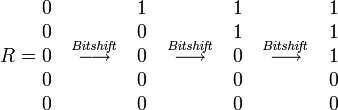
Inserts

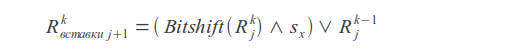
Deletions

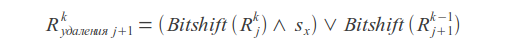
Replacements

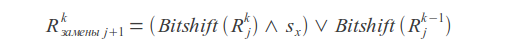
Resulting value


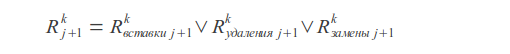
Where k is the number of errors, j is the character index, s _x is the character mask (in the mask, the unit bits are located at the positions corresponding to the positions of the given character in the request).
The match or mismatch of the query is determined by the most recent bit of the resulting vector R.

The high speed of this algorithm is provided by the bit parallelism of computations - in one operation it is possible to perform computations on 32 or more bits simultaneously.
At the same time, the trivial implementation supports searching for words no longer than 32. This restriction is determined by the width of the standard int type (on 32-bit architectures). You can use the types of large dimensions, but this may to some extent slow down the operation of the algorithm.

Despite the fact that the asymptotic time of operation of this algorithm O (kn) coincides with that of the linear method, it is much faster with long queries and the number of errors k is more than 2.

Testing

Testing was carried out on the text of 3.2 million words, the average word length - 10.

Exact search

Search time: 3562 ms

Search using the Levenshtein metric

Search time at k = 2 : 5728 ms
Search time at k = 5 : 8385 ms

Search using Bitap algorithm with Wu-Manber modifications

Search time at k = 2 : 5499 ms
Search time at k = 5 : 5928 ms

Obviously, a simple brute force using the metric, unlike the Bitap algorithm, strongly depends on the number of errors k .

However, if it comes to searching in large unchanged texts, the search time can be significantly reduced by performing preprocessing of such text, also called indexing .

Algorithms of fuzzy search with indexing (Offline)

A feature of all fuzzy search algorithms with indexing is that the index is based on a dictionary compiled from the source text or a list of records in a database.

These algorithms use different approaches to solving the problem - some of them use reduction to an exact search, others use metric properties to build various spatial structures, and so on.

First of all, the first step in the source text is to build a dictionary containing words and their positions in the text. Also, you can count the frequency of words and phrases to improve the quality of search results.

It is assumed that the index, as well as the dictionary, is entirely loaded into memory.

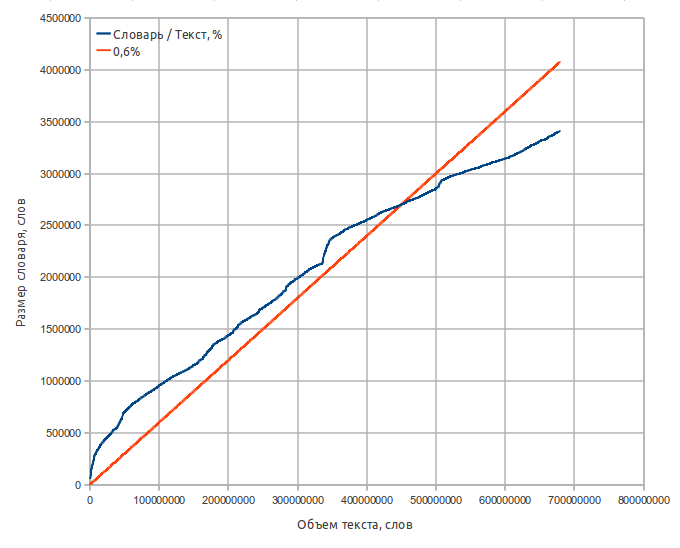
Technical characteristics of the dictionary:

• The source text is 8.2 gigabytes of Moshkov library materials ( lib.ru ), 680 million words;
• Dictionary size is 65 megabytes;
• The number of words - 3.2 million;
• The average word length is 9.5 characters;
• The mean square word length (may be useful in evaluating some algorithms) is 10.0 characters;
• Alphabet - capital letters AZ, without E (to simplify some operations). Words containing non-alphabetical characters are not included in the dictionary.

The dependence of the size of the dictionary on the volume of the text is not strictly linear — up to some volume, the basic framework of words is formed, ranging from 15% for 500 thousand words to 5% for 5 million, and then the dependence approaches linear, slowly decreasing and reaching 0.5% for 680 million words. Subsequent preservation of growth is provided in the majority due to rare words.

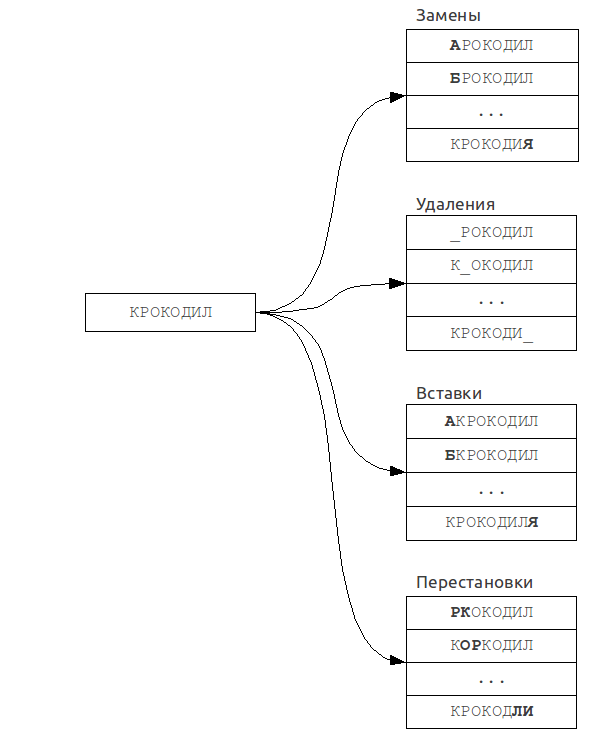
Sample extension algorithm

This algorithm is often used in spell-checking systems (i.e., in spell-checkers), where the size of the dictionary is small, or where the speed of work is not the main criterion.
It is based on the reduction of the fuzzy search problem to the exact search problem.

A set of “erroneous” words is constructed from the initial request, for each of which an exact search is then performed in the dictionary.



The time of its operation depends strongly on the number k of errors and on the size of the alphabet A, and in the case of using a binary dictionary search, it is:


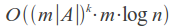
For example, if k = 1 and a word of length 7 (for example, “Crocodile”) in the Russian alphabet, the set of erroneous words will be about 450 in size, that is, 450 requests to the dictionary will have to be made, which is quite acceptable.
But already for k = 2, the size of such a set will be more than 115 thousand variants, which corresponds to a complete enumeration of a small dictionary, or 1/27 in our case, and, therefore, the work time will be long enough. At the same time, one should not forget that for each of these words it is necessary to conduct a search for an exact match in the dictionary.

Features:

The algorithm can be easily modified to generate “erroneous” variants according to arbitrary rules, and, moreover, it does not require any preprocessing of the dictionary, and, accordingly, additional memory.

Possible improvements:

It is possible to generate not all the set of “erroneous” words, but only those that are most likely to occur in a real situation, for example, words, taking into account common spelling errors or typing errors.

N-gram method

This method was invented quite a long time ago, and is the most widely used, since its implementation is extremely simple, and it provides fairly good performance. The algorithm is based on the principle:
"If the word A coincides with the word B, taking into account several errors, then with a high degree of probability they will have at least one common substring of length N".
These substrings of length N are called N-grams.
During indexing, the word is broken down into such N-grams, and then the word falls into the lists for each of these N-grams. During the search, the query is also divided into N-grams, and each of them is sequentially searched through the list of words containing such a substring.



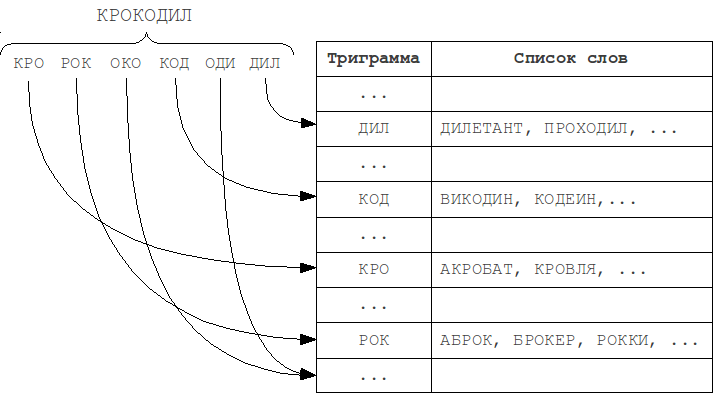
The most frequently used in practice are trigrams - substrings of length 3. The choice of a larger N value leads to a restriction on the minimum word length, at which error detection is already possible.

Features:

The N-gram algorithm does not find all possible misspelled words. If you take, for example, the word VOTKA, and decompose it into trigrams: VO KA → VO T O TK T KA, then you will notice that they all contain an error T. Thus, the word "VODKA" will not be found, because it does not contain any of these trigrams, and does not fall into the corresponding lists. Thus, the shorter the word length and the more errors it contains, the higher the chance that it will not fit into the lists corresponding to the N-grams of the query, and will not be present in the result.

Meanwhile, the N-gram method leaves full scope for using own metrics with arbitrary properties and complexity, but you have to pay for it - if you use it, there is a need for sequential enumeration of about 15% of the dictionary, which is quite a lot for large dictionaries.

Possible improvements:

You can break the N-gram hash tables by word length and by the position of the N-gram in the word (modification 1). As the length of the searched word and query cannot differ by more than k , so the positions of the N-gram in the word can differ by no more than k. Thus, it will be necessary to check only the table corresponding to the position of this N-gram in the word, as well as the k tables on the left and k tables on the right, i.e. total 2k + 1 adjacent tables.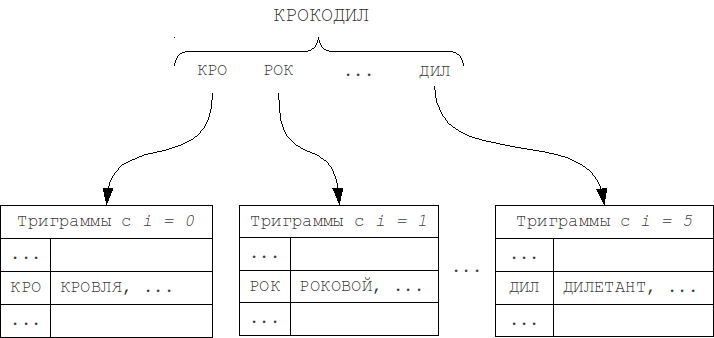



It is possible to slightly reduce the size of the set required for viewing by splitting the tables along the length of the word, and similarly looking only at the adjacent 2k + 1 tables (modification 2).

Signature hashing

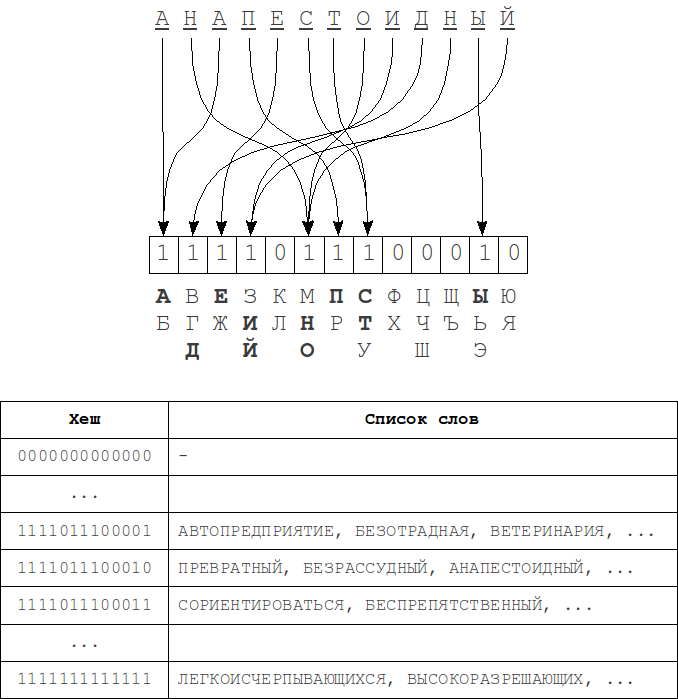
This algorithm is described in the article LM Boitsova. "Signature hashing". It is based on a fairly obvious representation of the word “structure” in the form of bit bits used as a hash (signature) in the hash table.

When indexing such hashes are calculated for each of the words, and the table corresponds to the list of dictionary words to this hash. Then, during the search, the hash is calculated for the request and all neighboring hashes that differ from the original in no more than k bits are searched. For each of these hashes, the list of words corresponding to it is searched.

The process of calculating the hash - each bit of the hash is associated with a group of characters from the alphabet. Bit 1 at position i in the hash means that the source word contains a symbol from the i-th alphabet group. The order of the letters in the word is absolutely irrelevant.



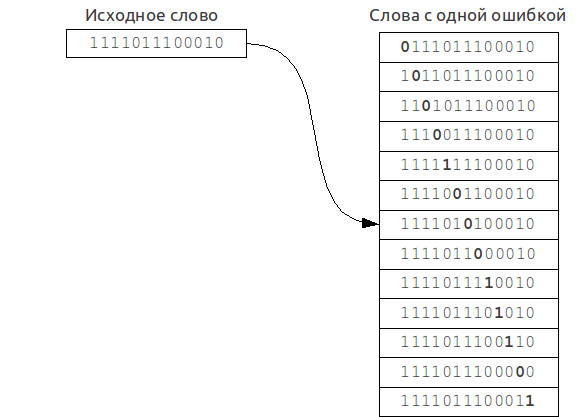
Deleting a single character either does not change the hash value (if there are still characters from the same alphabet group in the word), or the bit corresponding to this group changes to 0. When inserted, in the same way, either one bit will be 1 or no changes will be made. When replacing characters, everything is a bit more complicated - the hash can either remain completely unchanged or change in 1 or 2 positions. When permutations, no changes occur at all, because the order of the characters in constructing the hash, as noted earlier, is not taken into account. Thus, to fully cover the k errors, you need to change at least 2k bits in the hash.



Operating time, on average, with k "incomplete" (insertion, deletion and transposition, as well as a small part of the substitutions) errors:

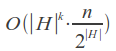
Features:

From the fact that replacing one character can change two bits at once, an algorithm that implements, for example, distortion of no more than 2 bits at the same time will not actually produce the full amount of results due to the absence of a significant part (depending on the ratio of the size of the hash to the alphabet) of the words with two substitutions (and the larger the size of the hash, the more often the replacement of the symbol will lead to distortion of two bits at once, and the less complete the result). In addition, this algorithm does not allow prefix searches.

BK-trees

The Burkhard-Keller trees are metric trees, the algorithms for constructing such trees are based on the metric property corresponding to the triangle inequality:



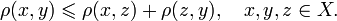
This property allows metrics to form metric spaces of arbitrary dimension. Such metric spaces are not necessarily Euclidean , for example, the Levenshtein and Damerau-Levenshtein metrics form non - Euclidean spaces. Based on these properties, you can build a data structure that searches in such a metric space, which is the Barkhard-Keller trees.

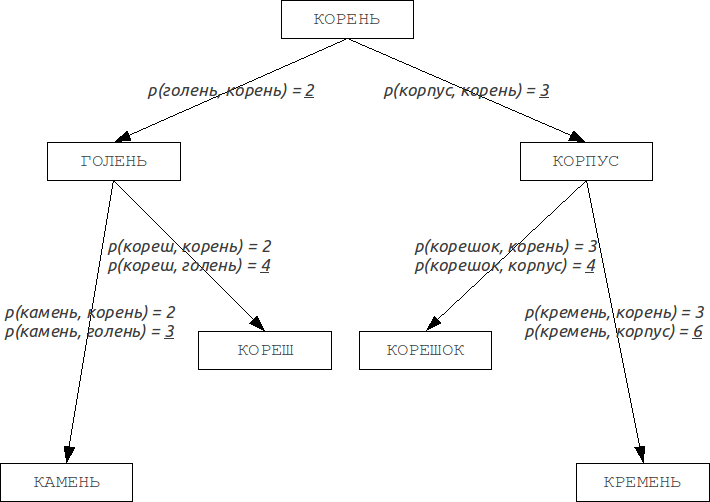
Improvements:

You can use the ability of some metrics to calculate the distance with a constraint, setting an upper limit equal to the sum of the maximum distance to the children of the vertex and the resulting distance, which will speed up the process a bit: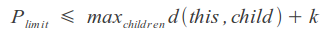

Testing

Testing was carried out on a laptop with Intel Core Duo T2500 (2GHz / 667MHz FSB / 2MB), 2Gb of RAM, OS - Ubuntu 10.10 Desktop i686, JRE - OpenJDK 6 Update 20.



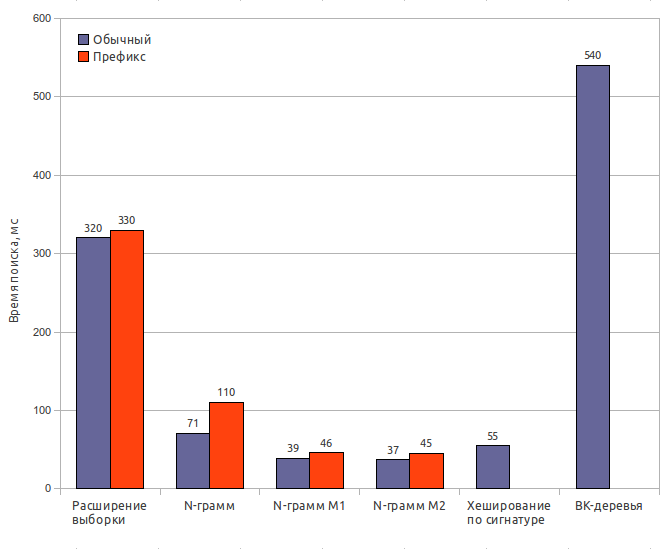
Testing was carried out using the Damerau-Levenshtein distance and the number of errors k = 2 . The size of the index is specified along with the dictionary (65 MB).

Sample extension

Index size: 65 MB
Search time: 320 ms / 330 ms
Completeness of results: 100%

N-gram (original)

Index size: 170 MB
Index creation time: 32 s
Search time: 71 ms / 110 ms
Completeness of results: 65%

N-gram (modification 1)

Index size: 170 MB
Index creation time: 32 s
Search time: 39 ms / 46 ms
Completeness of results: 63%

N-gram (modification 2)

Index size: 170 MB
Index creation time: 32 s
Search time: 37 ms / 45 ms
Completeness of results: 62%

Signature hashing

Index size: 85 MB
Index creation time: 0.6 s
Search time: 55 ms
Completeness of results: 56.5%

BK-trees

Index size: 150 MB
Index creation time: 120 s
Search time: 540 ms
Completeness of results: 63%

Total

Most fuzzy search algorithms with indexing are not truly sublinear (that is, having an asymptotic operating time of O (log n) or lower), and their speed of operation usually directly depends on N. Nevertheless, multiple improvements and improvements make it possible to achieve a sufficiently small working time, even with very large volumes of dictionaries.

There are also many more diverse and inefficient methods, based, among other things, on the adaptation of various, already-used techniques and techniques to this subject area. Among such methods is the adaptation of prefix trees (Trie) to fuzzy search problems , which I left unattended in view of its low efficiency. But there are algorithms based on original approaches, for example, the Maass-Novak algorithm , which, although it has sublinear asymptotic operation time, is extremely inefficient due to the huge constants behind such a time estimate, which manifest themselves in the form of a huge index size.

The practical use of fuzzy search algorithms in real search engines is closely related to phonetic algorithms , lexical stemming algorithms - extracting the base part from different word forms of the same word (for example, Snowball and Yandex mystem provide this functionality), as well as ranking based on statistical information or using sophisticated sophisticated metrics.

You can find my Java implementations on the http://code.google.com/p/fuzzy-search-tools link:

• Levenshtein distance (with clipping and prefix option);
• Damerau-Levenshtein distance (with clipping and prefix option);
• Bitap algorithm (Shift-OR / Shift-AND with modifications of Wu-Manber);
• Sample expansion algorithm;
• N-gram method (original and with modifications);
• Signature hashing method;
• BK-trees.

I wanted to make the code easy to understand, and at the same time quite effective for practical use. Squeezing the last juice from the JVM was not part of my task. Enjoy

It is worth noting that in the process of studying this topic, I had some own developments that allow us to reduce the search time by an order of magnitude due to a moderate increase in the size of the index and some restriction in the freedom to choose metrics. But that's another story.

References:

1. Source code for the article in Java. http://code.google.com/p/fuzzy-search-tools
2. Levenshtein distance. http://ru.wikipedia.org/wiki/Levenshteyn_Distance
3. Distance Damerau-Levenshteyn. http://en.wikipedia.org/wiki/Damerau–Levenshtein_distance
4. A good description of the Shift-Or with modifications Wu-Manber, however, in German. http://de.wikipedia.org/wiki/Baeza-Yates-Gonnet-Algorithmus
5. N-gram method. http://www.cs.helsinki.fi/u/ukkonen/TCS92.pdf
6. Signature hashing. http://itman.narod.ru/articles/rtf/confart.zip
7. The site of Leonid Moiseevich Boytsov, entirely devoted to fuzzy search. http://itman.narod.ru/
8. Implementation of Shift-Or and some other algorithms. http://johannburkard.de/software/stringsearch/
9. Fast Text Searching with Agrep (Wu & Manber). http://www.at.php.net/utils/admin-tools/agrep/agrep.ps.1
10. Damn Cool Algorithms - Levenshtein automaton, BK-trees, and some other algorithms. http://blog.notdot.net/2007/4/Damn-Cool-Algorithms-Part-1-BK-Trees
11. Java BK trees http://code.google.com/p/java-bk-tree/
12. The Maassa-Novak algorithm. http://yury.name/internet/09ia-seminar.ppt
13. SimMetrics Metrics Library. http://staffwww.dcs.shef.ac.uk/people/S.Chapman/simmetrics.html
14. SecondString metrics library. http://sourceforge.net/projects/secondstring/

: Fuzzy string search