Phonetic algorithms
Phonetic algorithms match two words with similar pronunciation to the same codes, which allows comparison and indexing of a set of such words based on their phonetic similarity.
It is often quite difficult to find an atypical last name in the database, for example:
It is very convenient to use such algorithms when searching databases in lists of people, in spelling checkers. They are often used in conjunction with fuzzy search algorithms (which undoubtedly deserve a separate article), providing users with a convenient search by first and last names in various databases, employee lists, and so on.
')
In this article I will discuss the most well-known algorithms, such as Soundex , Daitch-Mokotoff Soundex , NYSIIS , Metaphone , Double Metaphone , Russian Metaphone , Caverphone .
One of the first was the Soundex algorithm, invented by Robert Russell in the 10-x years of the last century. This algorithm (or rather, its American version) compares the words with a numerical index of the form A126 . The principle of its operation is based on the division of consonant letters into groups with sequence numbers, from which then the resulting value is compiled. Later, a number of improvements were also proposed.
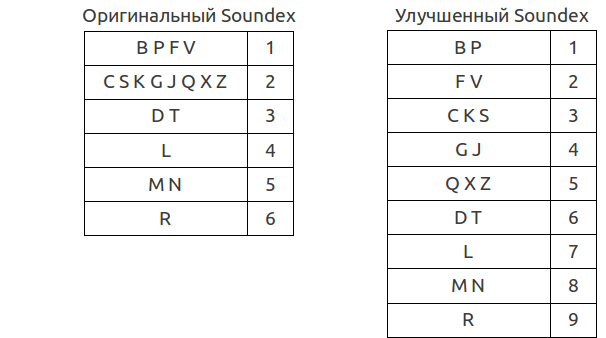
The first letter is saved, the subsequent letters are compared to the numbers in the table. Characters not represented in the table (and these are all vowels and some consonants) are ignored. Adjacent characters, or characters separated by the letters H or W , belonging to the same group, are written as one. The result is truncated to 4 characters. Missing positions are filled with zeros. It is easy to see that after all these procedures, only 7,000 different variations of such a code remain, which entails a multitude of completely dissimilar words that have the same Soundex code. Thus, the result in most cases includes a large number of “false positive” values.
In the improved version, as you can see, the letters are divided into more groups. In addition, no special attention is paid to the letters H and W, they are simply ignored. In addition, no operations with the result length are performed — the code does not have a fixed length and is not truncated.
Original Soundex:
D341 → Dedlovsky, Dedlovsky, Didilev, Ditelev, Dudalev, Dudolev, Dutlov, Dydalev, Dyatlov, Dyatlovich.
N251 → Nagimov, Nagmbetov, Nazimov, Nasimov, Nassonov, Nezhnov, Neznaev, Nesmeev, Nizhnevskiy, Nikonov, Nikonovich, Nisenblat, Nisenbaum, Nissenbaum, Noginov, Nochnov.
Superior Soundex:
N8030802 → Nasimov, Nassonov, Nikonov.
N80308108 → Nisenbaum, Nissenbaum.
N8040802 → Nagimov, Surge, Neganov, Noginov.
N804810602 → Nagmbetov.
N8050802 → Nazimov, Nezhnov, Sheath.
On average, there are 21 last names per one Soundex code value. In the case of an improved version of Soundex, only 2-3 names are converted to the same code.
Developed in 1970 as part of the New York State Identification and Intelligence System, this algorithm produces slightly better results relative to the original Soundex, using more complex rules for transforming the source word into the resulting code. This algorithm is designed to work with American surnames.
CASPARAVAS → Kasparavichus, Kasperovich, Kaspirovich.
CATNACAV → Katnikov, Cytnik, Tsotnikov.
LANSANC → Lenchenko, Leonchenko, Linchenko, Lunchenko, Lyamzenko.
PRADSC → Parish, Prohodsky, Prudsky, Prudsky, Prudsky.
STADNACAV → Stadnikov.
NYSIIS converts a little more than two last names to the same code.
This algorithm was developed in 1985 by two genealogists, Harry Motoff and Randy Deutsch, in an effort to achieve the best, relatively original Soundex, results when working with Eastern European (including Russian) surnames.
This algorithm has little to do with the original Soundex, except that the result is still a sequence of numbers, but now the first letter is also encoded.
It has much more complex conversion rules - now not only single characters but also sequences of several characters are involved in the formation of the resulting code. In addition, the result of the form 023689 provides about 600 thousand different variations of the code, which, together with complicated rules, reduces the number of “redundant”, i.e. "False positive" words in the resulting set.
Conversions are carried out according to the following table (the order of transformations corresponds to the order of the letter combinations in the table):
"Alternative" variants of letter combinations (used to generate several alternative codes from the source word):
CH → TCH
CK → TSK
C → TZ
J → DZH
095747 → Arhiptsev , Arhiptsov , Arkhipychev, Artsybasov, Artsybashev, Archibasov
095757 → Arkhipkov, Arhiptsev , Arhiptsov , Arhipychev
584360 → Galstyan, Galustyan, Gilstein, Glistin, Gluzdan, Golstein, Goldshtein, Goldstein, Kalustian, Khlistun, Khlystun, Khlyustin.
To the same code, this algorithm converts an average of 5 surnames.
Subsequently, Alexander Bader and Stephen Morse developed the Beider-Morse Name Matching Algorithm , aimed at reducing the number of "false positive" values relative to the Daitch-Mokotoff Soundex when working with Jewish (Ashkenazi) surnames.
The Metaphone algorithm (1990) has somewhat better characteristics, which differs from the previous algorithms in a slightly different approach to the coding process: it transforms the source word taking into account the rules of the English language, using noticeably more complex rules, and much less information is lost, since the letters do not split into groups. The resulting code is a set of characters from the set 0BFHJKLMNPRSTWXY , at the beginning of the word there can also be vowels from the set AEIOU .
AKXN → Agashin, Akachenok, Akishin, Aksionenko, Aksionov, Akchunaev, Akshanov, Akshentsev, Akshinsky, Akshintsev, Akshonov.
FSLX → Vasilishin, Vasilchak, Vasilchenko, Vasilchik, Vasilchikov, Vasilchenko, Vasilchuk, Vasiljushchenko.
SRFM → Serafimov, Serafimsky, Serafimchuk, Cereyfman.
The same Metaphone code value has an average of 6 last names.
Double Metaphone (2000) is somewhat different from other phonetic algorithms, generating not one but two codes (both up to 4 characters long) from the source word - one reflects the basic pronunciation of the word, the other the alternative version. It has a large number of different rules that take into account, among other things, the different origins of words, paying attention to Eastern European, Italian, Chinese words, and so on. The transformation rules are quite numerous, I will not publish them, and those who wish can read about them in an article in the journal Dr Dobbs .
JXRF → Gisharov .
KKRF → Gagarov, Kagarov, Kacharovsky, Kacherovsky , Kachurivsky, Kachurov, Kachurovsky, Kicherov, Kokarev, Kokourov, Kokourov, Kocharov, Kochurov, Kukarev, Tsakirov, Tsokurov, Tsugrov.
KXRF → Gisharov , Gocharov, Kacherov, Kacherovsky , Kasharevsky, Kocharov, Kocherev, Kocheryaev, Kochuraev, Kosharev, Kosherov.
PNFS → Banovsky, Bakhnovsky, Binevsky, Binyavsky, Buynovsky, Buyanovsky, Panevsky, Panovsky, Panovsky, Penevsky, Pinevsky, Piunovsky, Pikhnovsky.
Double Metaphone matches an average of 8-9 last names with the same code.
In 2002, an article by Pyotr Kankowski was published in the 8th edition of the Programmer magazine, describing his adaptation of the English version of the Metaphone algorithm to the severe Siberian frosts, bears and balalaikas. This algorithm transforms the original words in accordance with the rules and norms of the Russian language, taking into account the phonetic sound of unstressed vowels and possible “mergers” of consonants in pronunciation. It shows very good results in practice, despite the fact that it is based on fairly simple rules. All letters are divided into groups by sound - vowels and consonants ( vowels and consonants, respectively, in English terminology), deaf and voiced. Voiced consonants are converted into their corresponding deaf pair, the “merging” when pronouncing a sequence of letters is combined, and some other manipulations are performed. Below I will give a slightly modified version, which, unlike the original by Peter Kankowski, introduces rules related to the phonetic equivalence of C and TS or DC , and does not compress the endings - saving bytes is not our task.
In the case of Adolf Schwardsegger, the result of the work of the algorithm of the Russian Metaphone will be:
Thus, the algorithm in this case reflects the real phonetic similarity of these two last names.
VITAFSKIY → Vitavsky, Vitovsky.
VITINBIRK → Vitenberg, Wittenberg.
NASANAF → Nasanov, Nasonov, Nassonov, Nosonov.
PIRMAKAF → Permakov, Permyakov, Permyakov.
This algorithm converts to the same code an average of 1-2 surnames.
The Caverphone algorithm was developed in 2002 as part of one of the New Zealand projects for comparing data in old and new electoral lists; therefore, it is most focused on local pronunciation, although it gives quite acceptable results for Russian surnames.
KPRLN11111 → Gabrelyan, Gabrielyan, Gabrielyan, Kaparulin, Kapralin, Kaprelyan.
MSRFK11111 → Meizerovich, Misarovich, Misyurevich.
PLLF111111 → Balalaev, Balaliev, Balaluyev, Bilaliev, Bilalov, Bilyalov, Bolelov, Palilov, Polilov, Polulyakhov.
Caverphone matches the same code with about 4-5 names.
Most of these algorithms are implemented in a variety of languages, including C, C ++, Java, C #, and PHP. Some of them, such as Soundex and Metaphone, are integrated or implemented as plug-ins for many popular DBMSs, and are also used as part of full-fledged search engines, for example, Apache Lucene . The area of their application is quite specific, because a significant increase in convenience for users can be achieved only when searching for names, but nevertheless, their competent use is a plus for search engines.
It is often quite difficult to find an atypical last name in the database, for example:
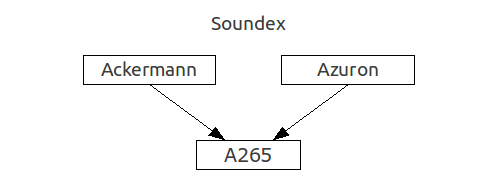
- Lech, look in our database for Adolph Schvardsenegger ,In this case, the use of phonetic algorithms (especially in combination with fuzzy matching algorithms) can significantly simplify the task.
- Shvortsegir ? There's no such thing!
It is very convenient to use such algorithms when searching databases in lists of people, in spelling checkers. They are often used in conjunction with fuzzy search algorithms (which undoubtedly deserve a separate article), providing users with a convenient search by first and last names in various databases, employee lists, and so on.
')
In this article I will discuss the most well-known algorithms, such as Soundex , Daitch-Mokotoff Soundex , NYSIIS , Metaphone , Double Metaphone , Russian Metaphone , Caverphone .
Soundex
One of the first was the Soundex algorithm, invented by Robert Russell in the 10-x years of the last century. This algorithm (or rather, its American version) compares the words with a numerical index of the form A126 . The principle of its operation is based on the division of consonant letters into groups with sequence numbers, from which then the resulting value is compiled. Later, a number of improvements were also proposed.

The first letter is saved, the subsequent letters are compared to the numbers in the table. Characters not represented in the table (and these are all vowels and some consonants) are ignored. Adjacent characters, or characters separated by the letters H or W , belonging to the same group, are written as one. The result is truncated to 4 characters. Missing positions are filled with zeros. It is easy to see that after all these procedures, only 7,000 different variations of such a code remain, which entails a multitude of completely dissimilar words that have the same Soundex code. Thus, the result in most cases includes a large number of “false positive” values.

In the improved version, as you can see, the letters are divided into more groups. In addition, no special attention is paid to the letters H and W, they are simply ignored. In addition, no operations with the result length are performed — the code does not have a fixed length and is not truncated.
Examples
Original Soundex:
D341 → Dedlovsky, Dedlovsky, Didilev, Ditelev, Dudalev, Dudolev, Dutlov, Dydalev, Dyatlov, Dyatlovich.
N251 → Nagimov, Nagmbetov, Nazimov, Nasimov, Nassonov, Nezhnov, Neznaev, Nesmeev, Nizhnevskiy, Nikonov, Nikonovich, Nisenblat, Nisenbaum, Nissenbaum, Noginov, Nochnov.
Superior Soundex:
N8030802 → Nasimov, Nassonov, Nikonov.
N80308108 → Nisenbaum, Nissenbaum.
N8040802 → Nagimov, Surge, Neganov, Noginov.
N804810602 → Nagmbetov.
N8050802 → Nazimov, Nezhnov, Sheath.
On average, there are 21 last names per one Soundex code value. In the case of an improved version of Soundex, only 2-3 names are converted to the same code.
NYSIIS
Developed in 1970 as part of the New York State Identification and Intelligence System, this algorithm produces slightly better results relative to the original Soundex, using more complex rules for transforming the source word into the resulting code. This algorithm is designed to work with American surnames.
NYSIIS Code Calculation Algorithm
- Convert the beginning of the word according to the following rules:
MAC → MCC
KN → N
K → C
PH, PF → FF
SCH → SSS - Convert the end of a word according to the following rules:
EE → Y
IE → Y
DT, RT, RD, NT, ND → D - Then all letters, except the first, are converted according to the following rules:
EV → AF
A, E, I, O, U → A
Q → G
Z → S
M → N
KN → N
K → C
SCH → SSS
PH → FF
After vowels: remove H, convert W → A - Remove S at the end
- Convert AY at the end → Y
- Delete A at the end
- Trim to 6 characters (optional).
Examples
CASPARAVAS → Kasparavichus, Kasperovich, Kaspirovich.
CATNACAV → Katnikov, Cytnik, Tsotnikov.
LANSANC → Lenchenko, Leonchenko, Linchenko, Lunchenko, Lyamzenko.
PRADSC → Parish, Prohodsky, Prudsky, Prudsky, Prudsky.
STADNACAV → Stadnikov.
NYSIIS converts a little more than two last names to the same code.
Daitch-Mokotoff Soundex
This algorithm was developed in 1985 by two genealogists, Harry Motoff and Randy Deutsch, in an effort to achieve the best, relatively original Soundex, results when working with Eastern European (including Russian) surnames.
This algorithm has little to do with the original Soundex, except that the result is still a sequence of numbers, but now the first letter is also encoded.
It has much more complex conversion rules - now not only single characters but also sequences of several characters are involved in the formation of the resulting code. In addition, the result of the form 023689 provides about 600 thousand different variations of the code, which, together with complicated rules, reduces the number of “redundant”, i.e. "False positive" words in the resulting set.
Conversions are carried out according to the following table (the order of transformations corresponds to the order of the letter combinations in the table):
| Source letters | At the beginning | Behind the vowel | Rest |
| AI, AJ, AY, EI, EY, EJ, OI, OJ, OY, UI, UJ, UY | 0 | one | |
| AU | 0 | 7 | |
| IA, IE, IO, IU | one | ||
| EU | one | one | |
| A, UE, E, I, O, U, Y | 0 | ||
| J | one | one | one |
| SCHTSCH, SCHTSH, SCHTCH, SHTCH, SHCH, SHTSH, STCH, STSCH, STRZ, STRS, STSH, SZCZ, SZCS | 2 | four | four |
| SHT, SCHT, SCHD, ST, SZT, SHD, SZD, SD | 2 | 43 | 43 |
| CSZ, CZS, CS, CZ, DRZ, DRS, DSH, DS, DZH, DZS, DZ, TRZ, TRS, TRCH, TSH, TTSZ, TTZ, TZS, TSZ, SZ, TTCH, TCH, TTSCH, ZSCH, ZHSH, SCH, SH, TTS, TC, TS, TZ, ZH, ZS | four | four | four |
| SC | 2 | four | four |
| DT, D, TH, T | 3 | 3 | 3 |
| CHS, KS, X | five | 54 | 54 |
| S, Z | four | four | four |
| CH, CK, C, G, KH, K, Q | five | five | five |
| MN, NM | 66 | 66 | |
| M, N | 6 | 6 | 6 |
| FB, B, PH, PF, F, P, V, W | 7 | 7 | 7 |
| H | five | five | |
| L | eight | eight | eight |
| R | 9 | 9 | 9 |
CH → TCH
CK → TSK
C → TZ
J → DZH
Examples
095747 → Arhiptsev , Arhiptsov , Arkhipychev, Artsybasov, Artsybashev, Archibasov
095757 → Arkhipkov, Arhiptsev , Arhiptsov , Arhipychev
584360 → Galstyan, Galustyan, Gilstein, Glistin, Gluzdan, Golstein, Goldshtein, Goldstein, Kalustian, Khlistun, Khlystun, Khlyustin.
To the same code, this algorithm converts an average of 5 surnames.
Subsequently, Alexander Bader and Stephen Morse developed the Beider-Morse Name Matching Algorithm , aimed at reducing the number of "false positive" values relative to the Daitch-Mokotoff Soundex when working with Jewish (Ashkenazi) surnames.
Metaphone
The Metaphone algorithm (1990) has somewhat better characteristics, which differs from the previous algorithms in a slightly different approach to the coding process: it transforms the source word taking into account the rules of the English language, using noticeably more complex rules, and much less information is lost, since the letters do not split into groups. The resulting code is a set of characters from the set 0BFHJKLMNPRSTWXY , at the beginning of the word there can also be vowels from the set AEIOU .
Metaphone code calculation algorithm
- Delete all duplicate adjacent letters except the letter C.
- Start the words convert according to the following rules:
KN → N
GN → N
PN → N
AE → E
WR → R - Remove the letter B at the end if it goes after M.
- Replace C with the following rules.
On X: CIA → XIA, SCH → SKH, CH → XH
On S: CI → SI, CE → SE, CY → SY
On K: C → K - Replace D with the following rules.
On J: DGE → JGE, DGY → JGY, DGI → JGY
On T: D → T - Replace GH → H if this letter combination is not at the end and not before a vowel.
- Replace GN → N and GNED → NED if these letter combinations are at the end.
- Replace G with the following rules.
On J: GI → JI, GE → JE, GY → JY
on K: G → K - Remove all Hs after vowels, but not before vowels.
- Perform subsequent transformations by the rules:
CK → K
PH → F
Q → K
V → F
Z → S - Replace S with X:
SH → XH
SIO → XIO
SIA → XIA - Replace T with the following rules.
On X: TIA → XIA, TIO → XIO
On 0: TH → 0
Delete: TCH → CH - At the beginning of the word convert WH → W. If after W there is no vowel, then delete W.
- If X is at the beginning of a word, then convert X → S, otherwise X → KS
- Delete all Y that are not before vowels.
- Remove all vowels except the initial one.
Examples
AKXN → Agashin, Akachenok, Akishin, Aksionenko, Aksionov, Akchunaev, Akshanov, Akshentsev, Akshinsky, Akshintsev, Akshonov.
FSLX → Vasilishin, Vasilchak, Vasilchenko, Vasilchik, Vasilchikov, Vasilchenko, Vasilchuk, Vasiljushchenko.
SRFM → Serafimov, Serafimsky, Serafimchuk, Cereyfman.
The same Metaphone code value has an average of 6 last names.
Double Metaphone
Double Metaphone (2000) is somewhat different from other phonetic algorithms, generating not one but two codes (both up to 4 characters long) from the source word - one reflects the basic pronunciation of the word, the other the alternative version. It has a large number of different rules that take into account, among other things, the different origins of words, paying attention to Eastern European, Italian, Chinese words, and so on. The transformation rules are quite numerous, I will not publish them, and those who wish can read about them in an article in the journal Dr Dobbs .
Examples
JXRF → Gisharov .
KKRF → Gagarov, Kagarov, Kacharovsky, Kacherovsky , Kachurivsky, Kachurov, Kachurovsky, Kicherov, Kokarev, Kokourov, Kokourov, Kocharov, Kochurov, Kukarev, Tsakirov, Tsokurov, Tsugrov.
KXRF → Gisharov , Gocharov, Kacherov, Kacherovsky , Kasharevsky, Kocharov, Kocherev, Kocheryaev, Kochuraev, Kosharev, Kosherov.
PNFS → Banovsky, Bakhnovsky, Binevsky, Binyavsky, Buynovsky, Buyanovsky, Panevsky, Panovsky, Panovsky, Penevsky, Pinevsky, Piunovsky, Pikhnovsky.
Double Metaphone matches an average of 8-9 last names with the same code.
Russian Metaphone
In 2002, an article by Pyotr Kankowski was published in the 8th edition of the Programmer magazine, describing his adaptation of the English version of the Metaphone algorithm to the severe Siberian frosts, bears and balalaikas. This algorithm transforms the original words in accordance with the rules and norms of the Russian language, taking into account the phonetic sound of unstressed vowels and possible “mergers” of consonants in pronunciation. It shows very good results in practice, despite the fact that it is based on fairly simple rules. All letters are divided into groups by sound - vowels and consonants ( vowels and consonants, respectively, in English terminology), deaf and voiced. Voiced consonants are converted into their corresponding deaf pair, the “merging” when pronouncing a sequence of letters is combined, and some other manipulations are performed. Below I will give a slightly modified version, which, unlike the original by Peter Kankowski, introduces rules related to the phonetic equivalence of C and TS or DC , and does not compress the endings - saving bytes is not our task.
Algorithm for calculating the Russian Metaphone code
- For all vowels, do the following.
YO, IO, IT, IE → AND
Oh, I, I → A
E, E, E → I
Yu → U - For all consonants, followed by any consonant, except L , M , H, or P , or for consonants at the end of a word, hold a stun:
B → P
H → C
D → T
In → F
G → K - We stick together the TS and the DS in C :
TS → TS
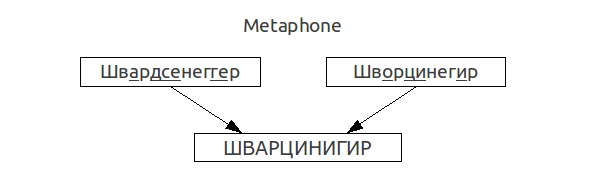
In the case of Adolf Schwardsegger, the result of the work of the algorithm of the Russian Metaphone will be:

Thus, the algorithm in this case reflects the real phonetic similarity of these two last names.
Examples
VITAFSKIY → Vitavsky, Vitovsky.
VITINBIRK → Vitenberg, Wittenberg.
NASANAF → Nasanov, Nasonov, Nassonov, Nosonov.
PIRMAKAF → Permakov, Permyakov, Permyakov.
This algorithm converts to the same code an average of 1-2 surnames.
Caverphone
The Caverphone algorithm was developed in 2002 as part of one of the New Zealand projects for comparing data in old and new electoral lists; therefore, it is most focused on local pronunciation, although it gives quite acceptable results for Russian surnames.
Caverphone code calculation algorithm
- Convert the name or surname to lower case (the algorithm is case sensitive).
- Remove the letters e at the end.
- Transform the beginning of the word according to the following table (relevant for local New Zealand names and surnames). The figure 2 means the time stamp for the consonant letter, which will subsequently be deleted.
cough rough tough enough gn mb cou2f rou2f tou2f enou2f 2n m2 - Perform character replacements according to the following table:
cq ci ce cy tch c q x v dg tio tia d ph b sh z 2q si se sy 2ch k k k f 2g sio sia t fh p s2 s - Replace all vowels at the beginning of the word with A , in other cases - with 3 . Thus, the number 3 serves as a timestamp for a vowel that will be used in subsequent transformations, and then will be deleted. After, it is necessary to make replacements in the following tables (notation: s + - several consecutive characters, ^ h - the character at the beginning of the line, w $ - the character at the end of the line):
j ^ y3 ^ y y 3gh3 gh g s + t + p + k + f + m + y Y3 A 3 3kh3 22 k S T P K F M n + w3 wh3 w $ w ^ h h r3 r $ r l3 l $ l N W3 Wh3 3 2 A 2 R3 3 2 L3 3 2 - Delete all digits 2 . If the number 3 remains at the end of the word, then replace it with A. Then delete all numbers 3 .
- Crop the word to 10 characters, or add up to 10 characters in units.
Examples
KPRLN11111 → Gabrelyan, Gabrielyan, Gabrielyan, Kaparulin, Kapralin, Kaprelyan.
MSRFK11111 → Meizerovich, Misarovich, Misyurevich.
PLLF111111 → Balalaev, Balaliev, Balaluyev, Bilaliev, Bilalov, Bilyalov, Bolelov, Palilov, Polilov, Polulyakhov.
Caverphone matches the same code with about 4-5 names.
Total
Most of these algorithms are implemented in a variety of languages, including C, C ++, Java, C #, and PHP. Some of them, such as Soundex and Metaphone, are integrated or implemented as plug-ins for many popular DBMSs, and are also used as part of full-fledged search engines, for example, Apache Lucene . The area of their application is quite specific, because a significant increase in convenience for users can be achieved only when searching for names, but nevertheless, their competent use is a plus for search engines.
Links
- Java code for the article. Yandex.Disk
- Implements Soundex, Refined Soundex, Metaphone, Double Metaphone, Caverphone in Java.
Apache commons codec - Implementing NYSIIS in Java. Project egothor
- The implementation of Daitch-Mokotoff Soundex in Java. http://joshualevy.tripod.com/genealogy/dmsoundex/dmsoundex.zip
- Description Soundex. http://en.wikipedia.org/wiki/Soundex
- Description Daitch-Mokotoff Soundex. http://www.jewishgen.org/infofiles/soundex.html
- Description of NYSIIS.
http://en.wikipedia.org/wiki/New_York_State_Identification_and_Intelligence_System - Description Metaphone. http://en.wikipedia.org/wiki/Metaphone
- Description Double Metaphone. http://www.drdobbs.com/article/184401251
- Description of Russian Metaphone. http://forum.aeroion.ru/topic461.html
- Description Caverphone. http://en.wikipedia.org/wiki/Caverphone
- Online demo Soundex. http://www.gedpage.com/soundex.html
- NYSIIS online demo. http://www.dropby.com/NYSIIS.html
- Online demo Daitch-Mokotoff Soundex. http://stevemorse.org/census/soundex.html
- Online demo Metaphone. http://www.searchforancestors.com/utility/metaphone.php
Source: https://habr.com/ru/post/114947/
All Articles