Ray Tracer of four-dimensional space

Recently I did a simple raytracer of 3-dimensional scenes. It was written in JavaScript and was not very fast. For fun, I wrote a raytracer on C and made him a 4-dimensional rendering mode - in this mode, he can project a 4-dimensional scene on a flat screen. Under the cat you will find several videos, some pictures and a raytracer code.





')

Why write a separate program for drawing a 4-dimensional scene? You can take a regular raytracer, slip him a 4D scene and get an interesting picture, but this picture will not be a projection of the whole scene on the screen. The problem is that the scene has 4 dimensions, and the screen is only 2 and when the raytracer starts the rays through the screen, it covers only the 3-dimensional subspace and the screen will only see a 3-dimensional cut of the 4-dimensional scene. A simple analogy: try to project a 3-D scene onto a 1-D segment.



It turns out that a 3-dimensional observer with 2-dimensional vision cannot see the entire 4-dimensional scene - at best, he will see only a small part. It is logical to assume that the 4-dimensional scene is more convenient to look at with 3-dimensional vision: a certain 4-dimensional observer looks at an object and on its 3-dimensional retinal analogue a 3-dimensional projection is formed. My program will rayten this three-dimensional projection. In other words, my raytracer depicts what a 4-dimensional observer sees with his 3-dimensional vision.

Features 3-dimensional view

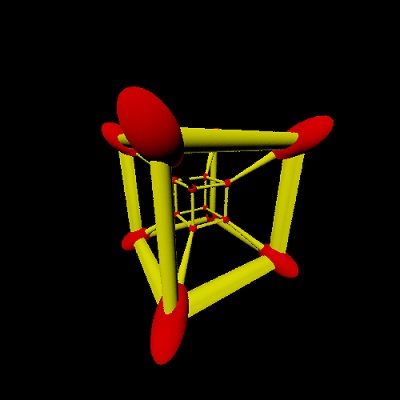
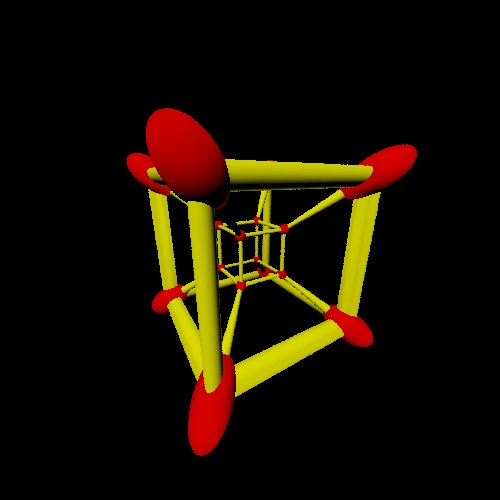
Imagine that you are looking at a circle of paper that is right in front of your eyes - in which case you will see a circle. If this circle is put on the table, then you will see an ellipse. If you look at this circle from a distance, it will appear smaller. Similarly for three-dimensional vision: a four-dimensional ball will appear to the observer as a three-dimensional ellipsoid. Below are a couple of examples. On the first, 4 identical mutually perpendicular cylinders rotate. On the second, the framework of a 4-dimensional cube rotates.













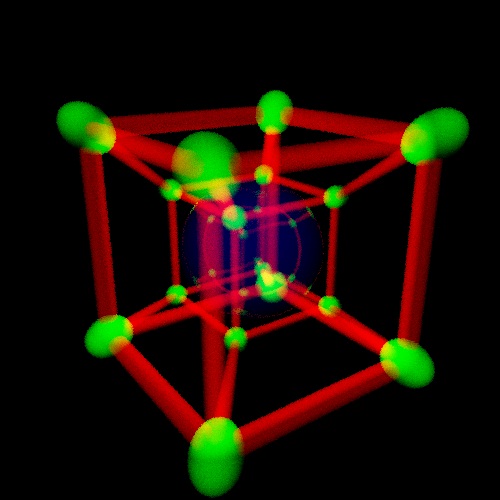
Let's go to the reflections. When you look at a ball with a reflective surface (a Christmas-tree toy, for example), the reflection is drawn on the surface of the sphere. Also for 3-dimensional view: you look at a 4-dimensional ball and reflections are drawn as if on its surface. Only here the surface of a 4-dimensional ball is three-dimensional, so when we look at a 3-dimensional projection of a ball, the reflections will be inside, not on the surface. If we make the reystrayser release the beam and find the nearest intersection with the 3-dimensional projection of the ball, we will see a black circle - the surface of the three-dimensional projection will be black (this follows from Fresnel formulas). It looks like this:







For 3D, this is not a problem, because the whole 3-D ball is visible to it and the internal points are visible as well as those on the surface, but I need to somehow convey this effect on a flat screen, therefore I made an additional Raytracer mode when he considers that three-dimensional objects are smoky: the beam passes through them and gradually loses energy. It turns out like this:











The same is true for shadows: they do not fall to the surface, but inside 3-dimensional projections. It turns out that inside a 3-dimensional ball - a projection of a 4-dimensional ball - there can be a darkened area in the form of a projection of a 4-dimensional cube, if this cube casts a shadow on the ball. I haven't figured out how to convey this effect on a flat screen.

Optimization

Raytrasit 4-dimensional scene is more complicated than 3-dimensional: in the case of 4D you need to find the colors of the three-dimensional area, and not the flat. If you write a raytracer "in the forehead", its speed will be extremely low. There are a couple of simple optimizations that can reduce the rendering time of a 1000 × 1000 image to a few seconds.



The first thing that catches your eye when looking at such pictures is a bunch of black pixels. If you depict an area where a raytracer ray hits at least one object, it will turn out like this:







It can be seen that about 70% are black pixels, and that the white area is connected (it is connected because the 4-dimensional scene is connected). You can calculate pixel colors not in order, but guess one white pixel and make a fill from it. This will only tracerays white pixels + some black pixels that represent the 1-pixel border of the white area.



The second optimization is obtained from the fact that the figures - balls and cylinders - are convex. This means that for any two points in such a figure, the segment connecting them also lies entirely inside the figure. If the beam intersects a convex object, while point A lies inside the object and point B is outside, then the remainder of the beam from side B will not cross the object.

Some more examples

Here the cube rotates around the center. The ball of the cube does not apply, but on a 3-dimensional projection they can intersect.







In this video, the cube is stationary, and a 4-dimensional observer flies through the cube. That 3-dimensional cube that seems larger is closer to the observer, and the smaller one is further.







Below is the classic rotation in the planes of axes 1-2 and 3-4. Such a rotation is given by the product of two Givens matrices.

How does my raytracer

The code is written in ANSI C 99. You can download it here . I checked on ICC + Windows and GCC + Ubuntu.



The program accepts a text file with a scene description as input.

scene = { objects = -- list of objects in the scene { group -- group of objects can have an assigned affine transform { axiscyl1, axiscyl2, axiscyl3, axiscyl4 } }, lights = -- list of lights { light{{0.2, 0.1, 0.4, 0.7}, 1}, light{{7, 8, 9, 10}, 1}, } } axiscylr = 0.1 -- cylinder radius axiscyl1 = cylinder { {-2, 0, 0, 0}, {2, 0, 0, 0}, axiscylr, material = {color = {1, 0, 0}} } axiscyl2 = cylinder { {0, -2, 0, 0}, {0, 2, 0, 0}, axiscylr, material = {color = {0, 1, 0}} } axiscyl3 = cylinder { {0, 0, -2, 0}, {0, 0, 2, 0}, axiscylr, material = {color = {0, 0, 1}} } axiscyl4 = cylinder { {0, 0, 0, -2}, {0, 0, 0, 2}, axiscylr, material = {color = {1, 1, 0}} } 

Then parsit this description and creates a scene in its internal presentation. Depending on the dimension of space, it renders a scene and gets either a four-dimensional image as above in the examples, or a regular three-dimensional one. To turn a 4-dimensional raytracer into a 3-dimensional one, you need to change the vec_dim parameter from 4 to 3 in the vector.h file. You can also set it in the command line parameters for the compiler. Compilation in GCC:



cd /home/ username /rt/

gcc -lm -O3 *.c -o rt





Test run:



/home/ username /rt/rt cube4d.scene cube4d.bmp





If you compile the raytracer with vec_dim = 3, then it will give out a regular cube for the cube3d.scene scene.

How to make a video

For this, I wrote a script on Lua which for each frame calculated the rotation matrix and added it to the reference scene.

 axes = { {0.933, 0.358, 0, 0}, -- axis 1 {-0.358, 0.933, 0, 0}, -- axis 2 {0, 0, 0.933, 0.358}, -- axis 3 {0, 0, -0.358, 0.933} -- axis 4 } scene = { objects = { group { axes = axes, axiscyl1, axiscyl2, axiscyl3, axiscyl4 } }, } 

The group object in addition to the list of objects has two affine transformation parameters: axes and origin. By changing the axes you can rotate all the objects in the group.



Then the script called the compiled raytracer. When all the frames were rendered, the script called the mencoder and he collected video from individual images. The video was made in such a way that it could be put on auto-repeat - i.e. the end of the video is the same as the beginning. The script runs like this:



luajit animate.lua





And finally, in this archive there are 4 avi files 1000 × 1000. All of them are cyclic - you can put on auto-repeat and you get a normal animation.