Tip 23. Consider replacing associative containers with sorted vectors.
“Even if the guaranteed logarithmic search time suits you, standard associative containers are not always the best choice. Strangely enough, the standard associative containers for speed are often inferior to the banal vector container ”- C. Meyers“ Effective use of STL ”.
Many may be interested in the practical side of this advice, how much a sorted vector can actually be faster than associative containers. I was also interested in this question and I decided to conduct a small test and draw a couple of graphs so that everything fell into place.
A bit of theory, for starters (those who know what a vector and a map are, do not need to be read). A map in STL is an associative container for storing key-value pairs. The data in it is stored in sorted form, although the C ++ standard does not specify an implementation, most often the map is implemented as a red-black tree, in which each element stores pointers to two descendants. A vector in STL is simply a container of elements that ensures that the data stored in it is not fragmented. Effective search in it can be organized by sorting and further binary search. As in the first case, the search complexity is O (ln (n)). The difference in speed will differ due to better caching in the second case (the data is located locally, and less memory is needed for storage).
To compare the insertion speed and the search, a test program was written that measures two types - writing random values (random (3)) into containers, measuring time (using gettimeofday), and finding random values in the container for a certain time ( 10 c). Thus, the time it takes to insert data into the container and the number of searches in the container during the time interval is measured.
Tools:
Hardware: Dual-processor (Intel Xeon E5420) server without a swap file.
Software: Ubuntu server with kernel 2.6.28, gcc 4.3.3.
Compiling a project with the keys: -O3 -felide-constructors -fno-exceptions -fno-rtti -funroll-loops -ffast-math -fomit-frame-pointer -march = core2
Each test was run several times (N = 10), and the minimum, maximum, and average values of a certain parameter were recorded. During the tests, the difference in the obtained values was minimized (reducing the load on the server, installing cpu affinity).
')
Data obtained by inserting items into containers
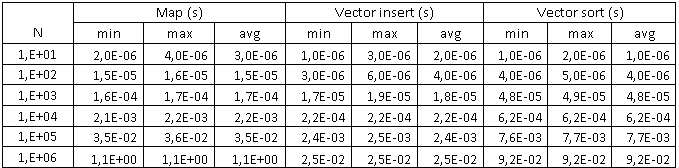
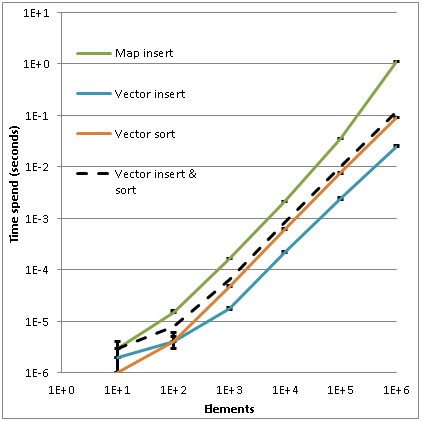
The first graph shows the dependence of the time of insertion and sorting for containers depending on the number of elements. Both scales are logarithmic, therefore, for clarity, another curve was constructed, showing the sum of the time of insertion and sorting for the vector - it is shown by a dotted line. Horizontal black lines show the error for each experiment - the maximum and minimum values. As can be seen for 1 million records, the time of insertion and sorting of a vector is approximately 10 times less (0.11 s) than for a map (1.1 s).
Data obtained by searching for items in containers
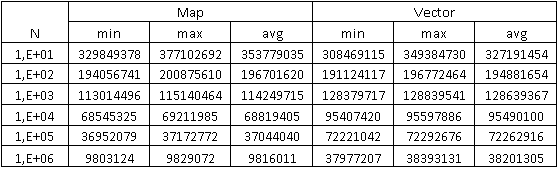
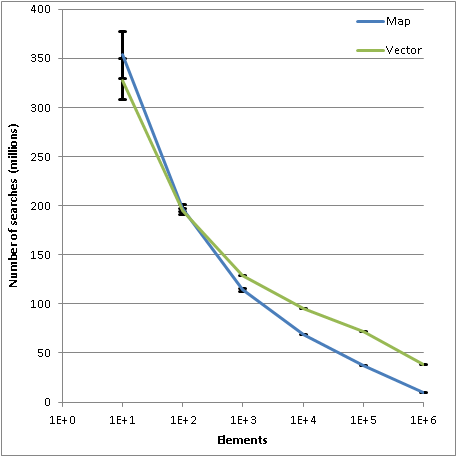
The second graph shows the dependence of the number of searches per unit of time (10 seconds) on the number of elements in the container. It can be seen that the search speed in the vector is higher, as it was supposed above, and by 1 million records the number of searches in a vector is approximately 3.9 times more than in the map.
From these tests, it can be seen that vector performance can be significantly (3.9 times) higher than the map, while filling the vector once and sorting it is also faster (10 times) than in the map. Thus, sorted vectors should be used in situations of rare data changes and frequent searches, for example, for data loaded during program start-up and subsequently rarely changing. And as always, one should not forget that premature optimization is evil.
Many may be interested in the practical side of this advice, how much a sorted vector can actually be faster than associative containers. I was also interested in this question and I decided to conduct a small test and draw a couple of graphs so that everything fell into place.
A bit of theory, for starters (those who know what a vector and a map are, do not need to be read). A map in STL is an associative container for storing key-value pairs. The data in it is stored in sorted form, although the C ++ standard does not specify an implementation, most often the map is implemented as a red-black tree, in which each element stores pointers to two descendants. A vector in STL is simply a container of elements that ensures that the data stored in it is not fragmented. Effective search in it can be organized by sorting and further binary search. As in the first case, the search complexity is O (ln (n)). The difference in speed will differ due to better caching in the second case (the data is located locally, and less memory is needed for storage).
To compare the insertion speed and the search, a test program was written that measures two types - writing random values (random (3)) into containers, measuring time (using gettimeofday), and finding random values in the container for a certain time ( 10 c). Thus, the time it takes to insert data into the container and the number of searches in the container during the time interval is measured.
Tools:
Hardware: Dual-processor (Intel Xeon E5420) server without a swap file.
Software: Ubuntu server with kernel 2.6.28, gcc 4.3.3.
Compiling a project with the keys: -O3 -felide-constructors -fno-exceptions -fno-rtti -funroll-loops -ffast-math -fomit-frame-pointer -march = core2
Each test was run several times (N = 10), and the minimum, maximum, and average values of a certain parameter were recorded. During the tests, the difference in the obtained values was minimized (reducing the load on the server, installing cpu affinity).
')
Data obtained by inserting items into containers


The first graph shows the dependence of the time of insertion and sorting for containers depending on the number of elements. Both scales are logarithmic, therefore, for clarity, another curve was constructed, showing the sum of the time of insertion and sorting for the vector - it is shown by a dotted line. Horizontal black lines show the error for each experiment - the maximum and minimum values. As can be seen for 1 million records, the time of insertion and sorting of a vector is approximately 10 times less (0.11 s) than for a map (1.1 s).
Data obtained by searching for items in containers


The second graph shows the dependence of the number of searches per unit of time (10 seconds) on the number of elements in the container. It can be seen that the search speed in the vector is higher, as it was supposed above, and by 1 million records the number of searches in a vector is approximately 3.9 times more than in the map.
From these tests, it can be seen that vector performance can be significantly (3.9 times) higher than the map, while filling the vector once and sorting it is also faster (10 times) than in the map. Thus, sorted vectors should be used in situations of rare data changes and frequent searches, for example, for data loaded during program start-up and subsequently rarely changing. And as always, one should not forget that premature optimization is evil.
Source: https://habr.com/ru/post/114518/
All Articles