Dynamic programming. Match model
Hello, Habrahabr. In this after I want to talk about dynamic programming on the example of solving one of the problems. I recently encountered this task on the Olympiad Portal (the link is listed at the end). Immediately get down to business.
Professor Samodelkin decided to make a three-dimensional model of cubes from matches using matches for the edges of the cubes. The length of the edge of each cube is equal to one match.
To build a model of three cubes, he used 28 matches.
What is the smallest number of matches needed to do it yourself to build a model of N cubes?
All numbers in the problem do not exceed 2 · 10 9 .
Technical conditions
')
Input data
One number N - the number of cubes.
Output
One number - the number of matches.
I solved this problem using dynamic programming, but it could be solved in other ways, and even just with a single formula - which we derive at the end.
“However, among reboring and some other tasks, one can distinguish a class of problems with one good property: having solutions of some subtasks (for example, for a smaller number n), one can find a solution to the original problem almost without overwhelming it.” - A class of problems that are solved by dynamic programming .
And our goal is to achieve a solution, according to the description of the dynamic programming tasks, in which the solution for the current parameters is based on the solution of the previous ones.
I have broken this task into 3 stages:
And so we set the conditions of the problem:
We need to find out the minimum number of matches that are needed to build a line of N squares with a side of 1 match.

To store the result, I will use the DP array.
Now we look at the picture and fill this array with numbers that need to be added to the solution for the i-1 case:
And the answer for N is the sum of the elements of the array DP from 0 to N , and immediately see the pattern - for DP [1]: = 4 , DP [> 1]: = 3
and derive the formula (N is always> 1, that is, natural):
Result (N) : = SUM (DP 1 -> DP N ) = 4+ (N-1) * 3
Task:
We need to find out the minimum number of matches that is necessary for constructing squares with a side of 1 match. You can build in 2 dimensions.
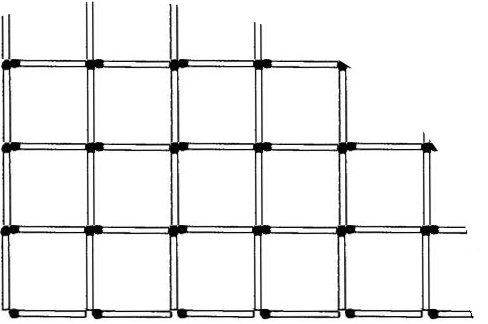
In 2D, we have a new problem: to the plane of what size, A x B, should we strive to minimize the number of matches? And as many have guessed, this is of course a square. But not everything is so simple, you need to simplify this idea.
If you look at the picture above, you can see that the most advantageous position for the new square will be that which has more neighbors, and in the optimal case it will be 2 neighbors.
That is, the best case will be built like this:
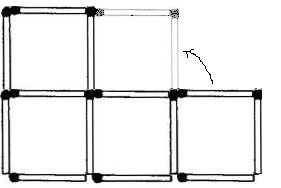
We can easily tell where to build the next cube if it does it by hand, but how to tell the computer about it?
If we take a leaflet and start building a certain plane from a square to minimize the number of edges, we will notice how we build:
Initially, it was a square 1x1 - 1 square, then extend to 2x1 - 2 squares, then:
2x2 - 3 and then 4 squares
3x2 - 5 and 6 squares
3x3 - 7,8,9 squares
Carefully look and see the pattern: we have the plane A x B to minimize the number of edges, the following to build the plane will be (A + 1) x B and then (A + 1) x (B + 1), the latter is a square, since we starting to build from 1 x 1
Write a table for the DP array:
Analyzing the table:
for DP [1] = 4
Next, when we add a new row, we make a new square using 3 matches and finish the square by 2 matches until the end of the row. Still not what does not resemble? Recall the case of 1D - the first square is 4 matches, the rest are 3, in this case it is the same extra row, but with an initial square of 3 matches and the rest of 2 matches.
Now the solution algorithm:
or so:
And the formula:
Result (N) : = 4 + 3 * (the number of full squares that are up to the number N without 1 + additional numbers that go before the full squares) + 2 * (everything else)
N SQRT : = int (sqrt (N)) - 1
N ADD : = N SQRT + 1 (if N <= N SQRT * (N SQRT +1))
Result (N) : = 4 + 3 * (N SQRT + N ADD ) + 2 * (NN SQRT -N ADD )
That got to 3D case
In the three-dimensional case, to minimize the number of matches to build, now already, the cubes need to tend to the construction of a large cube, but in intermediate versions it will be:
A x B x C -> (A + 1) x B x C -> (A + 1) x (B + 1) x C -> (A + 1) x (B + 1) x (C + 1)
the solution algorithm will be the same as in the 2D case, but taking into account some new features:
1D (N): = 5+ (N-1) * 3
2D (N): = the algorithm given above in the subsection, but with the correction - 2D (1): = 8
3D (N): = the algorithm given above in the 2D case, but taking into account the three-dimensionality - 3D (1): = 12, and with increasing coordinates we will change the result like this: Result: = Result + 2D (A * B * C / max (A, B, C)), i.e. it will be necessary to obtain 2D of the size of the added plane by changing the parameter of our new parallelepiped
And the formula for 3D
The formula will consist of the same parts as the formula for 2D, but also we will take into account not only full squares but also full Cubes.
Result (N) : = 12 + 8 * (3 * N full cubes + (0 or 1 or 2 depending on N)) + 5 * (2 * N full squares + (0 or 1 depending on N)) + 3 * N the rest
But, unfortunately, this formula is not entirely correct and requires more mental effort to think through some exceptions and amendments.
In the previous sections, we investigated what determines the minimization of matches for a cube / square, and based on this, we can make an algorithm of any dimension:
It is necessary to take into account how many matches the initial N-dimensional square consists of, and calculate how many matches you need to complete the construction of new elements.
We deduced the object dimension drag algorithm — at each iteration, increase by 1 the smallest dimension.
We also realized that when changing the size of an object, the value of the (N-1) -th measurement function should be added to the result of the size of the added plane
In creating a formula, you need to take into account the number of numbers in the N degree, N-1, N-2, etc. + take into account the features
E-olimp is an Internet portal of organizational and methodological support of remote programming olympiads for talented youth in educational institutions of Ukraine.
The task on the portal, which you can try to pass - need to register
Dynamic Programming Article
Task
Professor Samodelkin decided to make a three-dimensional model of cubes from matches using matches for the edges of the cubes. The length of the edge of each cube is equal to one match.
To build a model of three cubes, he used 28 matches.
What is the smallest number of matches needed to do it yourself to build a model of N cubes?
All numbers in the problem do not exceed 2 · 10 9 .
Technical conditions
')
Input data
One number N - the number of cubes.
Output
One number - the number of matches.
I solved this problem using dynamic programming, but it could be solved in other ways, and even just with a single formula - which we derive at the end.
“However, among reboring and some other tasks, one can distinguish a class of problems with one good property: having solutions of some subtasks (for example, for a smaller number n), one can find a solution to the original problem almost without overwhelming it.” - A class of problems that are solved by dynamic programming .
And our goal is to achieve a solution, according to the description of the dynamic programming tasks, in which the solution for the current parameters is based on the solution of the previous ones.
Decision
I have broken this task into 3 stages:
- Solve the problem for the 1D case and in it I will use a square with a side of 1 match, derive the formula
- Solve the problem for the 2D case and in it I will use the square with a match of 1 match, derive the formula
- Find the patterns in the 1D and 2D case and on the basis of them solve the problem for the 3D case, derive a formula for the 3D case
- Thoughts on the n-dimensional case
1D
And so we set the conditions of the problem:
We need to find out the minimum number of matches that are needed to build a line of N squares with a side of 1 match.

To store the result, I will use the DP array.
Now we look at the picture and fill this array with numbers that need to be added to the solution for the i-1 case:
| N: | 0 | one | 2 | 3 | four | five | 6 | 7 |
| DP: | 0 | four | 3 | 3 | 3 | 3 | 3 | 3 |
And the answer for N is the sum of the elements of the array DP from 0 to N , and immediately see the pattern - for DP [1]: = 4 , DP [> 1]: = 3
and derive the formula (N is always> 1, that is, natural):
Result (N) : = SUM (DP 1 -> DP N ) = 4+ (N-1) * 3
2D
Task:
We need to find out the minimum number of matches that is necessary for constructing squares with a side of 1 match. You can build in 2 dimensions.

In 2D, we have a new problem: to the plane of what size, A x B, should we strive to minimize the number of matches? And as many have guessed, this is of course a square. But not everything is so simple, you need to simplify this idea.
If you look at the picture above, you can see that the most advantageous position for the new square will be that which has more neighbors, and in the optimal case it will be 2 neighbors.
That is, the best case will be built like this:

We can easily tell where to build the next cube if it does it by hand, but how to tell the computer about it?
If we take a leaflet and start building a certain plane from a square to minimize the number of edges, we will notice how we build:
Initially, it was a square 1x1 - 1 square, then extend to 2x1 - 2 squares, then:
2x2 - 3 and then 4 squares
3x2 - 5 and 6 squares
3x3 - 7,8,9 squares
Carefully look and see the pattern: we have the plane A x B to minimize the number of edges, the following to build the plane will be (A + 1) x B and then (A + 1) x (B + 1), the latter is a square, since we starting to build from 1 x 1
Write a table for the DP array:
| N | one | 2 | 3 | four | five | 6 | 7 | eight | 9 |
| The size | 1 x 1 | 2 x 1 | 2 x 2 | 2 x 2 | 3 x 2 | 3 x 2 | 3 x 3 | 3 x 3 | 3 x 3 |
| DP | four | 3 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
Analyzing the table:
for DP [1] = 4
Next, when we add a new row, we make a new square using 3 matches and finish the square by 2 matches until the end of the row. Still not what does not resemble? Recall the case of 1D - the first square is 4 matches, the rest are 3, in this case it is the same extra row, but with an initial square of 3 matches and the rest of 2 matches.
| N for 2D | one | 2 | 3 | four | five | 6 | 7 | eight | 9 |
| N for 1D | one | one | one | 2 | one | 2 | one | 2 | 3 |
| The size | 1 x 1 | 2 x 1 | 2 x 2 | 2 x 2 | 3 x 2 | 3 x 2 | 3 x 3 | 3 x 3 | 3 x 3 |
| DP | four | 3 | 3 | 2 | 3 | 2 | 3 | 2 | 2 |
Now the solution algorithm:
DP[1]=4
A=1
B=1 // A x B
1 N A B DP 1D A B :
j=1 // DPfor1D, DPfor1D={3,2,2,2,2,2,2,2,...}
for i = 2 -> N
begin
if A*B<i
then begin
(A<B)?A++:B++
j=1
end
DP[i]:= DP[i-1]+DPfor1D[j]
j++
end
or so:
Result:= 4
newN:= 1
A:= 2
B:= 1
while newN <= N
begin
Result:= Result + 1D(min(A,B)) // 1D(N):=3+(N-1)*2 N >= 1, 0
(A<B)?A++:B++
newN=A*B
end
(A>B)?A--:B--
Result:= Result+ 1D(NA*B)
And the formula:
Result (N) : = 4 + 3 * (the number of full squares that are up to the number N without 1 + additional numbers that go before the full squares) + 2 * (everything else)
N SQRT : = int (sqrt (N)) - 1
N ADD : = N SQRT + 1 (if N <= N SQRT * (N SQRT +1))
Result (N) : = 4 + 3 * (N SQRT + N ADD ) + 2 * (NN SQRT -N ADD )
3D
That got to 3D case
In the three-dimensional case, to minimize the number of matches to build, now already, the cubes need to tend to the construction of a large cube, but in intermediate versions it will be:
A x B x C -> (A + 1) x B x C -> (A + 1) x (B + 1) x C -> (A + 1) x (B + 1) x (C + 1)
the solution algorithm will be the same as in the 2D case, but taking into account some new features:
1D (N): = 5+ (N-1) * 3
2D (N): = the algorithm given above in the subsection, but with the correction - 2D (1): = 8
3D (N): = the algorithm given above in the 2D case, but taking into account the three-dimensionality - 3D (1): = 12, and with increasing coordinates we will change the result like this: Result: = Result + 2D (A * B * C / max (A, B, C)), i.e. it will be necessary to obtain 2D of the size of the added plane by changing the parameter of our new parallelepiped
And the formula for 3D
The formula will consist of the same parts as the formula for 2D, but also we will take into account not only full squares but also full Cubes.
Result (N) : = 12 + 8 * (3 * N full cubes + (0 or 1 or 2 depending on N)) + 5 * (2 * N full squares + (0 or 1 depending on N)) + 3 * N the rest
But, unfortunately, this formula is not entirely correct and requires more mental effort to think through some exceptions and amendments.
Thoughts on the n-dimensional case
In the previous sections, we investigated what determines the minimization of matches for a cube / square, and based on this, we can make an algorithm of any dimension:
It is necessary to take into account how many matches the initial N-dimensional square consists of, and calculate how many matches you need to complete the construction of new elements.
We deduced the object dimension drag algorithm — at each iteration, increase by 1 the smallest dimension.
We also realized that when changing the size of an object, the value of the (N-1) -th measurement function should be added to the result of the size of the added plane
In creating a formula, you need to take into account the number of numbers in the N degree, N-1, N-2, etc. + take into account the features
Links
E-olimp is an Internet portal of organizational and methodological support of remote programming olympiads for talented youth in educational institutions of Ukraine.
The task on the portal, which you can try to pass - need to register
Dynamic Programming Article
Source: https://habr.com/ru/post/113720/
All Articles