Mathematical morphology
Using the search, I was surprised to find that at Habré there are no articles describing the apparatus of mathematical morphology, and this device is indispensable in the field of low-level image processing. If it is interesting to you, I ask under kat.
The term morphology refers to the description of the properties of the form and structure of any objects. In the context of machine vision, this term refers to the description of the properties of the shape of regions in an image. The operations of mathematical morphology were originally defined as operations on sets, but it soon became clear that they were also useful in the tasks of processing a set of points in a two-dimensional space. Objects in the image are represented by sets in mathematical morphology. It is easy to notice that the set of all background pixels of a binary image is one of the options for its full description.
First of all, mathematical morphology is used to extract some properties of an image that are useful for its presentation and description. For example, contours, skeletons, convex hulls. Also of interest are the morphological methods used at the stages of preliminary and final image processing. For example, morphological filtration, thickening or thinning.
The input data for the apparatus of mathematical morphology are two images: processed and special, depending on the type of operation and the problem being solved. Such a special image is called primitive or structural element. As a rule, the structural element is much smaller than the processed image. A structural element can be considered a description of a region with some form. It is clear that the form can be any, as long as it can be represented as a binary image of a given size. In many image processing packages, the most common structural elements have special names: BOX [H, W] - a rectangle of a given size, DISK [R] - a disk of a given size, RING [R] - a ring of a given size.
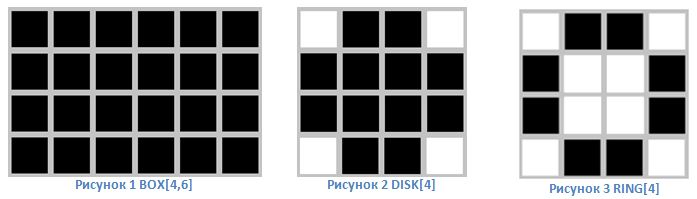
The result of morphological processing depends both on the size and configuration of the original image, and on the structural primitive.
The size of the structural element is usually 3 * 3, 4 * 4 or 5 * 5 pixels. This is due to the main idea of morphological processing, in the process of which the characteristic details of the image are sought. The required detail is described by a primitive, and as a result of morphological processing, you can emphasize or delete such details on the entire image.
One of the main advantages of morphological processing is its simplicity: we get a binarized image both at the entrance and at the exit of the processing procedure. Other methods, as a rule, first receive a halftone from the original image, which is then reduced to a binary one using the threshold function.
The main operations of mathematical morphology are building up, erosion, closure and opening. These names reflect the essence of operations: building increases the image area, and erosion makes it smaller, the closing operation allows you to close the internal openings of the area and eliminate bays along the border of the area, the opening operation helps to get rid of small fragments protruding outside the area near its border. Next will be presented the mathematical definitions of morphological operations.
Before proceeding to the operations of morphology, it makes sense to consider the set-theoretic operations that underlie mathematical morphology.
The union of two sets A and B, which is denoted by C = A∪B, is by definition the set of all elements belonging to either the set A, or the set B, or both sets simultaneously. Similarly, the intersection of two sets A and B, which is denoted by C = A∩B, is by definition the set of all elements belonging simultaneously to both sets A and B. The complement of set A is the set of elements not contained in A: A c = {w | w∉A}. The difference of two sets A and B is denoted A \ B and is defined as follows: A \ B = {w│w∈A, w∉B} = A∩B c . This set consists of elements A which are not included in set B.
Consider all of the above operations on a specific example.

The operation of transferring X t of a set of pixels X to a vector t is given in the form X t = {x + t | x∈X}. Consequently, the transfer of a set of single pixels on a binary image shifts all the pixels of a set by a specified distance. The transfer vector t can be specified as an ordered pair (∆r, ∆c), where ∆r is the transfer vector component in the row direction, and ∆c is the transfer vector component in the column direction of the image.

The following operations we will look at a specific example. Suppose we have the following binary image and structural element:
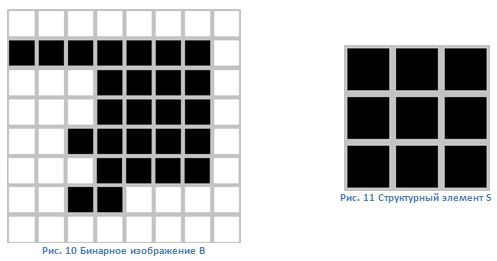
The structural element S is applied to all pixels of the binary image. Each time when the origin of the structural element is combined with a single binary pixel, the transfer and the subsequent logical addition with the corresponding pixels of the binary image are applied to the entire structural element. The results of logical addition are written to the output binary image, which is initially initialized to zero values.

When performing an erosion operation, the structural element also passes through all the pixels of the image. If at some position each unit pixel of the structural element coincides with the unit pixel of the binary image, then the logical addition of the central pixel of the structural element with the corresponding pixel of the output image is performed.

As a result of applying the erosion operation, all objects smaller than the structural element are erased, objects connected by thin lines become disconnected and the sizes of all objects decrease.
The erosion operation is useful for removing small objects and various noises, but this operation has a drawback - all the remaining objects are reduced in size. This effect can be avoided if, after an erosion operation, a build-up operation is applied with the same structural element.
Breaking out all objects that are smaller than the structural element, but at the same time helps to avoid a strong reduction in the size of objects. Also, the opening is ideal for removing lines whose thickness is less than the diameter of the structural element. It is also important to remember that after this operation the contours of the objects become smoother.

If we first apply the extension operation to the image, then we will be able to get rid of small holes and crevices, but at the same time there will be an increase in the contour of the object. To avoid this increase allows the operation of erosion, performed immediately after building with the same structural element.

One of the typical applications of binary morphology is the selection of components on a binary image, in which the shape and dimensions satisfy the specified constraints. In many such tasks, it is possible to build a structural element that, after being applied to the binary image, removes the components that do not satisfy the constraints and leaves several single pixels corresponding to the components that satisfy the constraints. But for subsequent processing may require components entirely, and not only their fragments remaining after erosion. To solve this problem, a conditional expansion operation was introduced.
The set obtained as a result of erosion is cyclically increased by the structural element S, and at each step the result is reduced to a subset of pixels that have single values in the original image B. The conditional extension operation is explained in the figure below. In this figure, the binary image B was eroded by the element V to select components containing vertical fragments 3 pixels in height. The resulting C image has two such components. To select these components entirely, the image C is conditionally expanded by the element D relative to the original image B.

Morphological operations can also be used to highlight the boundaries of a binary object. This operation is very important, because the border is a complete, and at the same time, a very compact description of the object.
It is easy to see that the boundary points have at least one background pixel in their neighborhood. Thus, applying the erosion operator with a structural element containing all possible neighboring elements, we will remove all boundary points ... Then the boundary will be obtained using the operation of the set difference between the original image and the image obtained as a result of erosion.

Thus, we have reviewed the basic operations of mathematical morphology, and several ways to apply them. I hope this device will be useful to you in further activities.
Basic definitions
The term morphology refers to the description of the properties of the form and structure of any objects. In the context of machine vision, this term refers to the description of the properties of the shape of regions in an image. The operations of mathematical morphology were originally defined as operations on sets, but it soon became clear that they were also useful in the tasks of processing a set of points in a two-dimensional space. Objects in the image are represented by sets in mathematical morphology. It is easy to notice that the set of all background pixels of a binary image is one of the options for its full description.
First of all, mathematical morphology is used to extract some properties of an image that are useful for its presentation and description. For example, contours, skeletons, convex hulls. Also of interest are the morphological methods used at the stages of preliminary and final image processing. For example, morphological filtration, thickening or thinning.
The input data for the apparatus of mathematical morphology are two images: processed and special, depending on the type of operation and the problem being solved. Such a special image is called primitive or structural element. As a rule, the structural element is much smaller than the processed image. A structural element can be considered a description of a region with some form. It is clear that the form can be any, as long as it can be represented as a binary image of a given size. In many image processing packages, the most common structural elements have special names: BOX [H, W] - a rectangle of a given size, DISK [R] - a disk of a given size, RING [R] - a ring of a given size.

The result of morphological processing depends both on the size and configuration of the original image, and on the structural primitive.
The size of the structural element is usually 3 * 3, 4 * 4 or 5 * 5 pixels. This is due to the main idea of morphological processing, in the process of which the characteristic details of the image are sought. The required detail is described by a primitive, and as a result of morphological processing, you can emphasize or delete such details on the entire image.
One of the main advantages of morphological processing is its simplicity: we get a binarized image both at the entrance and at the exit of the processing procedure. Other methods, as a rule, first receive a halftone from the original image, which is then reduced to a binary one using the threshold function.
Basic operations
The main operations of mathematical morphology are building up, erosion, closure and opening. These names reflect the essence of operations: building increases the image area, and erosion makes it smaller, the closing operation allows you to close the internal openings of the area and eliminate bays along the border of the area, the opening operation helps to get rid of small fragments protruding outside the area near its border. Next will be presented the mathematical definitions of morphological operations.
Union, intersection, addition, difference
Before proceeding to the operations of morphology, it makes sense to consider the set-theoretic operations that underlie mathematical morphology.
The union of two sets A and B, which is denoted by C = A∪B, is by definition the set of all elements belonging to either the set A, or the set B, or both sets simultaneously. Similarly, the intersection of two sets A and B, which is denoted by C = A∩B, is by definition the set of all elements belonging simultaneously to both sets A and B. The complement of set A is the set of elements not contained in A: A c = {w | w∉A}. The difference of two sets A and B is denoted A \ B and is defined as follows: A \ B = {w│w∈A, w∉B} = A∩B c . This set consists of elements A which are not included in set B.
Consider all of the above operations on a specific example.

Transfer
The operation of transferring X t of a set of pixels X to a vector t is given in the form X t = {x + t | x∈X}. Consequently, the transfer of a set of single pixels on a binary image shifts all the pixels of a set by a specified distance. The transfer vector t can be specified as an ordered pair (∆r, ∆c), where ∆r is the transfer vector component in the row direction, and ∆c is the transfer vector component in the column direction of the image.

Build-up, erosion, closure, opening
The following operations we will look at a specific example. Suppose we have the following binary image and structural element:

Building up
The structural element S is applied to all pixels of the binary image. Each time when the origin of the structural element is combined with a single binary pixel, the transfer and the subsequent logical addition with the corresponding pixels of the binary image are applied to the entire structural element. The results of logical addition are written to the output binary image, which is initially initialized to zero values.

Erosion
When performing an erosion operation, the structural element also passes through all the pixels of the image. If at some position each unit pixel of the structural element coincides with the unit pixel of the binary image, then the logical addition of the central pixel of the structural element with the corresponding pixel of the output image is performed.

As a result of applying the erosion operation, all objects smaller than the structural element are erased, objects connected by thin lines become disconnected and the sizes of all objects decrease.
Breaking
The erosion operation is useful for removing small objects and various noises, but this operation has a drawback - all the remaining objects are reduced in size. This effect can be avoided if, after an erosion operation, a build-up operation is applied with the same structural element.
Breaking out all objects that are smaller than the structural element, but at the same time helps to avoid a strong reduction in the size of objects. Also, the opening is ideal for removing lines whose thickness is less than the diameter of the structural element. It is also important to remember that after this operation the contours of the objects become smoother.

Short circuit
If we first apply the extension operation to the image, then we will be able to get rid of small holes and crevices, but at the same time there will be an increase in the contour of the object. To avoid this increase allows the operation of erosion, performed immediately after building with the same structural element.

Conditional build-up
One of the typical applications of binary morphology is the selection of components on a binary image, in which the shape and dimensions satisfy the specified constraints. In many such tasks, it is possible to build a structural element that, after being applied to the binary image, removes the components that do not satisfy the constraints and leaves several single pixels corresponding to the components that satisfy the constraints. But for subsequent processing may require components entirely, and not only their fragments remaining after erosion. To solve this problem, a conditional expansion operation was introduced.
The set obtained as a result of erosion is cyclically increased by the structural element S, and at each step the result is reduced to a subset of pixels that have single values in the original image B. The conditional extension operation is explained in the figure below. In this figure, the binary image B was eroded by the element V to select components containing vertical fragments 3 pixels in height. The resulting C image has two such components. To select these components entirely, the image C is conditionally expanded by the element D relative to the original image B.

Selection of boundaries
Morphological operations can also be used to highlight the boundaries of a binary object. This operation is very important, because the border is a complete, and at the same time, a very compact description of the object.
It is easy to see that the boundary points have at least one background pixel in their neighborhood. Thus, applying the erosion operator with a structural element containing all possible neighboring elements, we will remove all boundary points ... Then the boundary will be obtained using the operation of the set difference between the original image and the image obtained as a result of erosion.

Thus, we have reviewed the basic operations of mathematical morphology, and several ways to apply them. I hope this device will be useful to you in further activities.
')
Source: https://habr.com/ru/post/113626/
All Articles