Four-dimensional rendering: features, problems, solutions

In the comments to the article “Raytracer on JavaScript”, its author ankh1989 told about plans to write a raytracer for four-dimensional space. Some of my thoughts on this topic, I will try to present here.


')
So, let us have a scene in four-dimensional space. It consists of three-dimensional surfaces (polyhedra, spheres, cylinders, etc.), which are somehow colored and have a reflective and scattering ability. We want to display it on a flat (two-dimensional) image.

How can I do? Options may be:

1) build a three-dimensional section of the scene. We regard it as an ordinary 3D scene, and render it according to the laws of three-dimensional space.

2) We project 4D on 3D (for example, parallel projection). We consider that the visible points of the projection inherit the properties of their originals, and, again, we perform 3D rendering.

3) Perform a central projection of 4D on 3D using the four-dimensional ray tracing algorithm. We get a three-dimensional array of pixels. Now somehow we project it on 2D. There are such options:

3a) choose any direction, and on each line going in this direction, we find the first filled pixel (parallel orthogonal projection). The color of this pixel will give the point color of the final image.

3b) the same, but using the central projection.

3c, d) we take the projection from (3a, b), but instead of taking the color of the first pixel of the line, we average all the colors that fall on the line.

The first two approaches are rejected as uninteresting (although in some cases they may be useful). And consider, for example, option 3b.



So, we have a camera located at the origin, and directed towards Ow = (0,0,0,1). It projects a point with coordinates (x, y, z, w) into (p, q, r) = (x / w, y / w, z / w). Only the points with w> 0 are visible.

The second camera is located in three-dimensional space somewhere on the Or axis (point (0,0, -a)) and projects a point (p, q, r) onto a two-dimensional screen, to a point (u, v) = (p / (a + r), q / (a ​​+ r)). Substituting the values ​​of p, q, r from the first formula, we get that (u, v) = (x / (z + a * w), y / (z + a * w)). This means that instead of two central projections, we just have to do with one - we just need to turn the camera. The second projection will be orthogonal — along an axis perpendicular to both the screen and the axis of the camera. Thus, options (3a) and (3b) are equivalent.

Now let's take a closer look at what these projections are. It is easy to understand that information about the rays coming from a certain flat angle gets into each pixel of the screen. There are one-dimensional such rays, and either we take them all (and, for example, average them - these will be options (3c, d), or we will choose one of the rays that came not from emptiness, for example, the leftmost one - these will be options (3a, b ).



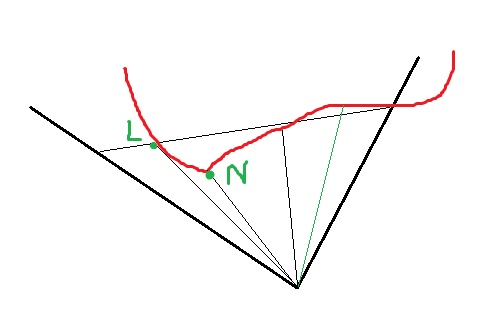
I didn’t like the option of the “leftmost point”: the OL line touches the object, and what we will see the 4D viewer would call the silhouette of the scene. Therefore, I decided to try a less common option — consider points of a scene that fell into a flat angle and take the color of the point nearest the camera. This closest point (when the boundaries of the angle are calculated) can be quickly found for any base object, after which tracing can be performed only for it - it turns out one trace per pixel, which is quite fast.

What happened?

First, I placed all the objects of the scene (including the camera) in the same plane w = 0. Naturally, the result of rendering does not differ from three-dimensional (only the quality is worse, I didn’t try very hard):



Then, without moving objects, I began to turn the camera in four dimensions. After the first shift, the result was as follows:



It can be seen that, firstly, the shadow of the green ball has disappeared, and secondly, the reflections of the red and green balls have disappeared in a large sphere! This happened because the spheres nearest to the camera point became different, not those in which there is a reflection of the balls.

In addition, the shape of the stand has changed. Now it can be seen that it is not flat, but three-dimensional, in fact it consists of 5 * 5 * 3 = 75 3D cubes.



After the next turn, the picture changed even more: two balls were drowned in the stand, only one was left - and that one half plunged.



And finally, the rotation is 90 degrees from the starting position: now we are looking from the w direction. And again we see one side of the stand, measuring 3 * 5.

Second experience. Put the camera back in place, and move the balls in the w direction (in different directions). It can be seen that the reflections of the red and green balls in the large ball have disappeared, and in addition, the size of the reflection of the red ball in the plane has sharply decreased. With shadows, too, something is not in order:



After turning the reflection disappeared completely:



For the next scene I used a new object - “tubes with a spherical section”. If you put 4 of these tubes in different orientations on a plane, you get this:



What a strange object is in the foreground, I do not understand. In my opinion, this is a hole. Or an error in the program.

After the first turn the reflections disappeared:



And after the second tube drowned, but the reflections returned!



The fourth scene is a rib model of tesseract consisting of balls and spherical tubes. On the first frame of the balls there are only 8: we look from this side that they close each other:



Note the reflection in the plane. It consists of 8 green spheres - these are sections of tubes that fall on the plane w = 0.

After turning the camera, all 16 vertices became visible, and the reflection in the sphere became unpredictable:



After the next turn, the cube is half drowned:



And then he emerged from the other side, but crossed with the mirror sphere:



And this is an attempt to place a cube in the space with spheres and look at its shadow.



By and large, there is nothing to look at.

So, it is clear that with the selected projection, the result is unpredictable, and we see only a part of the surface of the objects — and if there are interesting details on it, then they hide from us. Probably, for fuller pictures one will have to use averaging over many rays. Hope that 100 rays per angle will be enough.