Search strings and related questions
Hello, dear community! Recently on Habré a good overview article about different substring search algorithms in a string jumped. Unfortunately, there were no detailed descriptions of any of the mentioned algorithms. I decided to fill this gap and describe at least a couple of those that can potentially be remembered. Those who still remember the course of algorithms from the institute, apparently, will not find anything new for themselves.
At first I would like to prevent the question “why the hell is this necessary? everything is already written. ” Yes, it is written. But firstly, it is useful to know how the tools you use work at a lower level in order to better understand their limitations, and secondly, there are quite large adjacent areas where the strstr () function working from the box will not be enough. And thirdly, you may not be able to drive and will have to develop a mobile platform with an inferior runtime, and then it’s better to know what you are signing up for if you decide to supplement it yourself (to make sure that this is not a spherical problem in a vacuum, just try wcslen () and wcsstr () from Android NDK).
The fact is that the obvious way, which formulates everything as “take and search”, is by no means the most effective, but for such a low-level and relatively part-called function, this is important. So, the plan is:
The canonical version of the problem looks like this: we have the string A ( text ). It is necessary to check whether there is a substring X ( pattern ) in it, and if so, where it begins. That is exactly what the strstr () function does in C. In addition, you can also ask to find all the occurrences of the sample. Obviously, the problem makes sense only if X is not longer than A.
For simplicity, further explanation will introduce a couple of concepts at once. What a string everyone probably understands is a sequence of characters, perhaps an empty one. Symbols , or letters, belong to a certain set, which is called the alphabet (this alphabet, generally speaking, may not have anything in common with the alphabet in the everyday sense). Line length | A | - this is obviously the number of characters in it. The prefix of the string A [ ..i ] is a string of i first characters of the string A. The string suffix A [ j .. ] is the string from | A | -j + 1 last characters. The substring from A will be denoted as A [ i..j ] , and A [ i ] - the i-th character of the string. Question about empty suffixes and prefixes, etc. do not touch - it is not difficult to deal with them in place. There is also such a thing as seninel , a unique symbol not found in the alphabet. It is denoted by the $ symbol and complements the allowable alphabet with such a symbol (this is in theory, in practice it is easier to apply additional checks than to invent such a symbol that could not appear in the input strings).
In the calculations we will count the characters in the string from the first position. Code writing is traditionally easier to count from zero. The transition from one to another is not difficult.
')
Direct search, or, as it is often said, “just take and search” is the first solution that comes to the mind of an inexperienced programmer. The point is simple: follow the tested string A and look for the occurrence of the first character of the search string X in it . When we find, we make a hypothesis that this is the very desired entry. It then remains to check in turn all subsequent characters of the pattern for matching with the corresponding characters of string A. If they all matched, then here it is, right in front of us. But if any of the characters did not match, then nothing remains but to recognize our hypothesis as incorrect, which brings us back to the character following the occurrence of the first character from X.
Many people are mistaken at this point, considering that they should not go back, but it is possible to continue processing line A from the current position. Why it is not so easy to demonstrate by the example of the search X = "AAAB" in A = "AAAAB" . The first hypothesis will lead us to the fourth symbol A : "AAAAB" , where we will find a discrepancy. If you do not roll back, then the entry, we will not find, although it is.
Incorrect hypotheses are inevitable, and due to such rollbacks under bad circumstances, it may turn out that we checked every character in A about | X | time. That is, the computational complexity is the complexity of the algorithm O (| X || A |). So the search for a phrase in a paragraph may be delayed ...
To be fair, it should be noted that if the lines are small, then such an algorithm can work faster than the “correct” algorithms at the expense of a more predictable processor behavior.
One of the categories of correct ways to search for a string is reduced to calculating in some sense the correlation of two strings. First, we note that the task of comparing two lines began is simple and clear: we compare the corresponding letters until we find a discrepancy or one of the lines ends. Consider the set of all suffixes of the string A : A [ | A | .. ] A [ | A | -1 .. ] , ... A [ 1 .. ] . We will compare the beginning of the string itself with each of its suffixes. Comparison can reach the end of the suffix, or break on some character due to a mismatch. The length of the matched part is called the component of the Z-function for a given suffix.
That is, a Z-function is a vector of lengths of the greatest common prefix of a string with its suffix. Wow! An excellent phrase when you need to confuse or assert oneself, but to understand what it is, it is better to look at an example.
The original string is "ababcaba" . By comparing each suffix with the line itself, we get a label for the Z-function:
The suffix prefix is nothing more than a substring, and the Z-function is the length of the substrings that occur simultaneously in the beginning and in the middle. Considering all the values of the components of the Z-function, you can notice some regularities. First, it is obvious that the value of the Z-function does not exceed the length of the string and coincides with it only for the “full” suffix A [ 1 .. ] (and therefore this value does not interest us - we will omit it in our reasoning). Secondly, if there is a single character in the string, it can only match itself, which means it divides the line into two parts, and the value of the Z-function can never exceed the length of the shorter part.
It is proposed to use these observations as follows. Suppose in the line "ababcabacacab" we want to search for "abca" . We take these lines and concatenate, inserting the Sentinel between them: “abca $ ababcabacacab” . The vector of the Z-function looks like this:
If we discard the value for the full suffix, then the presence of the centinela limits Z i to the length of the desired fragment (it is the smaller half of the line in the sense of the problem). But if this maximum is reached, it is only in the positions of the substring entry. In our example, the quadruples mark all the positions of the occurrence of the search string (note that the found plots are located overlapping with each other, but all the same, our reasoning remains true).
Well, that means if we can quickly build a vector of the Z-function, then a search with it for all occurrences of a string is reduced to finding the value of its length in it. That's just if you calculate the Z-function for each suffix, then it will be clearly not faster than the solution "in the forehead." It helps us that the value of the next element of the vector can be found based on the previous elements.
Suppose we somehow calculated the values of the Z-function up to the corresponding i-1st symbol. Consider a certain position r <i, where we already know Z r .
So Z r characters from this position are exactly the same as at the beginning of the line. They form the so-called Z-block. We will be interested in the rightmost Z-block, that is, the one who ends the farthest (the very first does not count). In some cases, the rightmost block may be zero length (when none of the non-empty blocks cover i-1, then the rightmost one will be i-1st, even if Z i-1 = 0).
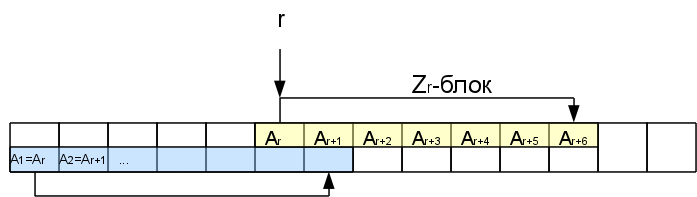
When we consider the subsequent characters inside this Z-box, it makes no sense to compare the next suffix from the very beginning, since part of this suffix has already been encountered at the beginning of the line, which means it has already been processed. It will be possible to immediately skip the characters right up to the end of the Z-block.
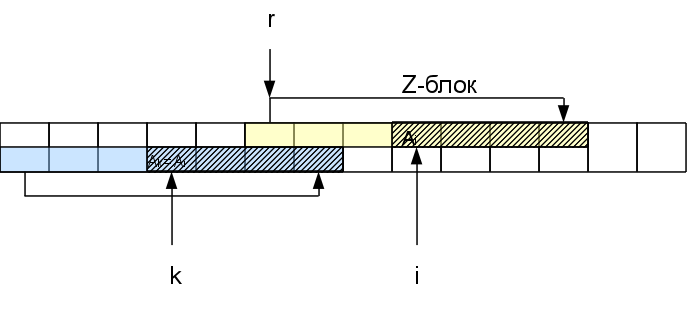
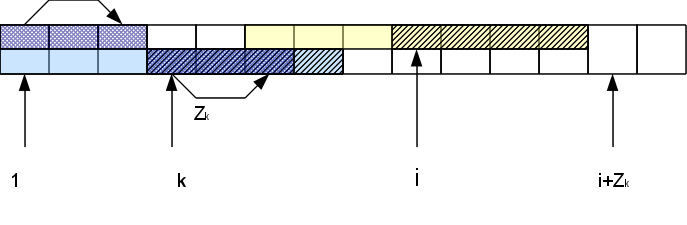
Namely, if we consider the i-th character in the Zr-block, that is, the corresponding character at the beginning of the line at position k = i-r + 1. The function Z k is already known. If it is less than the distance Z r - (ir) remaining to the end of the Z-block, then we can immediately be sure that the whole area of coincidence for this symbol lies inside the r-block of the Z-block and the result will be the same as in the beginning of the line: Z i = Z k . If Z k > = Z r - (ir), then Z i is also greater than or equal to Z r - (ir). To find out how much more it is, we will need to check the symbols following the Z-block. Moreover, in case of coincidence of these characters with the corresponding at the beginning of the line, Z i is increased by h: Z i = Z k + h. As a result, we may have a new right-most Z-block (if h> 0).
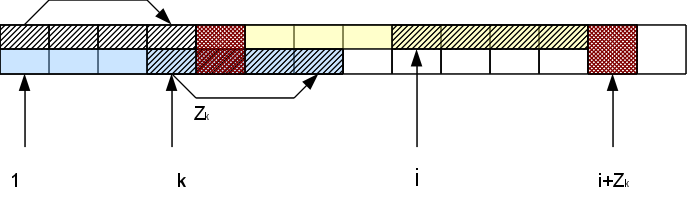
Thus, we have to compare characters only to the right of the rightmost Z-block, and due to successful comparisons, the block “moves” to the right, and unsuccessful ones report that the calculation for this position is over. This provides us with the construction of the entire vector of the Z-function in a time linear in the line length.
Applying this algorithm to search for substrings we obtain the complexity of the time O (| A | + | X |), which is much better than the product, which was in the first version. True, we had to store the vector for the Z-function, which would take additional memory of order O (| A | + | X |). In fact, if you do not need to find all occurrences, but only one is enough, then you can get by with O (| X |) memory, since the length of the Z-block still cannot be more than | X |, except that you can not continue processing the string after the first occurrence.
Finally, an example of a function that calculates the Z-function. Just a model option without any tricks.
Despite the logical simplicity of the previous method, a more popular is another algorithm, which in some sense is the inverse of the Z-function - the Knut-Morris-Pratt algorithm (CMP). We introduce the concept of prefix function . The prefix function for the i-th position is the length of the maximum string prefix, which is shorter than i and which matches the suffix of the prefix of length i. If the definition of the Z-function didn’t hit the opponent outright, then with this combo you will definitely be able to put it in place :) And in human language it looks like this: take every possible string prefix and look at the longest match beginning with the end of the prefix (disregarding the trivial match with myself). Here is an example for ababcaba :
Again, we observe a number of properties of the prefix function. First, the values are bounded above by their number, which follows directly from the definition - the prefix length must be greater than the prefix function. Secondly, the unique symbol in the same way divides the string into two parts and limits the maximum value of the prefix-function to the length of the smaller part - because everything that is longer will contain a unique, nothing else equal symbol.
From here we get the conclusion that interests us. Suppose we did reach at some element of this theoretical ceiling. This means that such a prefix has ended here, that the initial part coincides with the final part and one of them represents the “complete” half. It is clear that in the prefix the complete half should be in front, which means with this assumption it should be the shorter half, the maximum we reach on the longer half.
Thus, if, as in the previous part, we concatenate the desired line with the one in which we are looking through the Sentinel, then the point of entry of the length of the required substring in the component of the prefix function will correspond to the place where the entry ends. Take our example: in the string “ababcabacacab” we are looking for “abca” . The concatenated version of abca $ ababcabacacab . The prefix function looks like this:
Again, we found all occurrences of the substring in one fell swoop - they end in four positions. It remains to understand how to effectively calculate this prefix function. The idea of the algorithm is slightly different from the idea of constructing a Z-function.

The very first value of the prefix function is obviously 0. Suppose we calculated the prefix function to the i-th position inclusive. Consider the i + 1st character. If the value of the prefix function in the i-th position is P i , then the prefix A [ ..P i ] coincides with the substring A [ iP i + 1..i ] . If the symbol A [ P i +1 ] coincides with A [ i + 1 ] , then we can safely write down that Pi + 1 = Pi + 1. But if not, then the value can be either less or the same. Of course, when P i = 0 there is no place to decrease much, so in this case P i + 1 = 0. Suppose that P i > 0. Then there is the prefix A [ ..P i ] in the string, which is equivalent to the substring A [ iP i + 1..i ] . The desired prefix function is formed within these equivalent sections plus the character being processed, which means we can forget about the entire line after the prefix and leave only the given prefix and i + 1st character - the situation will be identical.
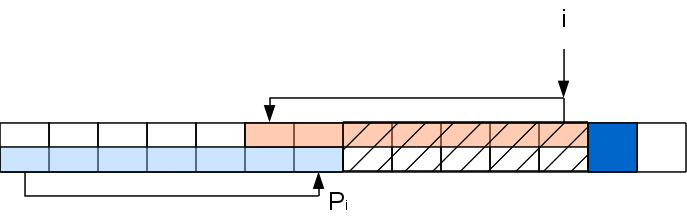
The task at this step has been reduced to a task for a line with a cut out center line: A [ ..P i ] A [ i + 1 ] , which can be solved recursively in the same way (although tail recursion is not a recursion at all, but a cycle). That is, if A [ P P i +1 ] coincides with A [ i + 1 ] , then P i + 1 = P P i +1, otherwise, we again throw out part of the line from consideration, etc. Repeat the procedure until we find a match or do not reach 0.
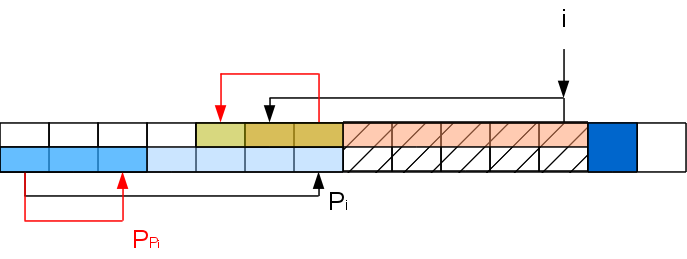
The repetition of these operations should be alerted - it would seem that there are two nested cycles. But it is not. The fact is that a nested loop with a length of k iterations reduces the prefix function in the i + 1 position by at least k-1, and in order to increase the prefix function to such a value, you need at least k-1 times successfully match the letters by processing k-1 characters. That is, the cycle length corresponds to the interval between the execution of such cycles and therefore the complexity of the algorithm is still linear in the length of the processed line. With memory, this is the same situation as with the Z-function - linear in the length of the line, but there is a way to save. In addition, there is a convenient fact that the characters are processed sequentially, that is, we are not obliged to process the entire line if we have already received the first entry.
Well, for example, a snippet of code:
Despite the fact that the algorithm is more intricate, its implementation is even simpler than for the Z-function.
Then there will be just a lot of letters that do not limit the search tasks to strings and that there are other tasks and other solutions, so if anyone is not interested, then you can not read further. This information is just for reference, in case of need, at least to realize that “everything is already stolen before us” and not reinvent the bicycle.
Although the above algorithms guarantee linear execution time, the title of the “default algorithm ” was given to the Boyer-Moore algorithm . On average, it also gives linear time, but also has a better constant for this linear function, but that is on average. There are “bad” data on which he is no better than the simplest “head-on” comparison (well, just like with qsort). It is extremely confused and will not be considered - all the same I do not remember. There are a number of exotic algorithms that are focused on natural language processing and rely in their optimizations on the statistical properties of words in a language.
Well, well, we have an algorithm that somehow or another O (| X | + | A |) is looking for a substring in the string. Now imagine that we are writing a guest book engine. We have a list of forbidden swear words (it is clear that this will not help, but the task is just for example). We are going to filter messages. We will look for each of the forbidden words in the message and ... this will take O (| X 1 | + | X 2 | + ... + | X n | + n | A |). Somehow so-so, especially if the dictionary of "mighty expressions" of "great and mighty" is very "mighty." For this case, there is a way to pre-process the dictionary of the required strings, that the search will occupy only O (| X 1 | + | X 2 | + ... + | X n | + | A |), and this can be significantly less, especially if the messages are long.
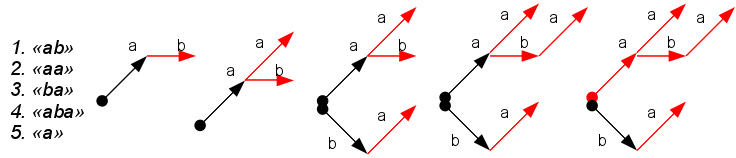
Such preprocessing is reduced to building a boron (trie) from a dictionary: a tree starts at some fictitious root, nodes correspond to letters of words in a dictionary, the depth of a tree node corresponds to the number of a letter in a word. The nodes where the word from the dictionary ends is called terminal and is labeled in some way (in red in the figure).
The resulting tree is an analogue of the prefix function of the CMP algorithm. With it, you can find all occurrences of all vocabulary words in a phrase. It is necessary to go through the tree, checking for the presence of the next symbol in the form of a tree node, simultaneously noting the encountered terminal vertices - these are occurrences of words. If there is no corresponding node in the tree, then, like in the ILC, a rollback takes place higher up the tree using special links. This algorithm is called the Aho-Corasica algorithm . The same scheme can be used to search during input and prediction of the next character in electronic dictionaries.
In this example, the construction of boron is simple: we simply add words to the boron in turn (nuances only with additional references for “kickbacks”). There are a number of optimizations aimed at reducing the memory use of this tree (the so-called boron compression - skipping sections without branching). In practice, these optimizations are almost optional. The disadvantage of this algorithm is its alphabet dependence: the time to process the node and the memory occupied depends on the number of potential children, which is equal to the size of the alphabet. For large alphabets, this is a serious problem (imagine a set of Unicode characters?). You can read more about all this in this habratopic or using GoogleIndex - the benefit of information on this subject is a lot.
Now look at another task. If in the previous one we knew in advance what we would have to find in the incoming data later, here it is exactly the opposite: we were given a line in advance, in which we would be searched, but what they would be looking for was unknown, but they would be searched a lot. A typical example is a search engine. The document in which the word is searched is known in advance, but the words that are searched there, are strewn on the go. The question is, again, how instead of O (| X 1 | + | X 2 | + ... + | X n | + n | A |) get O (| X 1 | + | X 2 | + ... + | X n | + | A |)?
It is proposed to build a bur in which will be all possible suffixes of the existing string. Then the search for a pattern will be reduced to checking the presence of a path in the tree corresponding to the desired pattern. If you build such a forest by searching all the suffixes, then this procedure can take O (| A | 2 ) time, and there is a lot of memory. But, fortunately, there are algorithms that allow you to build such a tree at once in a compressed form - a suffix tree , and to do it in O (| A |). Recently on Habré was about this article , so that those interested can read about the algorithm Ukkonen there.
Poorly in a suffix tree, as usual, there are two things: the fact that it is a tree and the fact that the nodes of the tree are alphabetically dependent. The suffix array is spared from these shortcomings. The essence of the suffix array is that if all the suffixes of the string are sorted, then the search for the substring will be reduced to the search for a group of adjacent suffixes by the first letter of the desired pattern and further refinement of the range by the subsequent ones. At the same time, there is no need to keep the suffixes in sorted form, it is enough to store the positions in which they begin in the original data. True, the time dependences of this structure are somewhat worse: a single search will do O (| X | + log | A |) if you think and do everything neatly, and O (| X | log | A |) if you do not bother. For comparison, in a tree for a fixed alphabet O (| X |). But the fact that this is an array, and not a tree, can improve the situation with memory caching and make it easier for the predictor of processor transitions. A suffix array is built in linear time using the Kärkkäinen-Sanders algorithm (sorry, but I have no idea how it should sound in Russian). Today it is one of the most popular methods of indexing strings.
We will not touch on the issues of approximate search for strings and analysis of the degree of similarity here - it is too big an area to be stuffed into this article. Just to mention that people there did not eat bread for nothing, and came up with many different approaches, so if you run into a similar task, find and read. Quite possibly this problem has already been solved.
Thanks to those who read! And for those who read to here, thank you very much!
UPD: Added a link to the informative article about boron (it’s a ray, it’s a prefix tree, it’s a loaded tree, it’s a trie).
At first I would like to prevent the question “why the hell is this necessary? everything is already written. ” Yes, it is written. But firstly, it is useful to know how the tools you use work at a lower level in order to better understand their limitations, and secondly, there are quite large adjacent areas where the strstr () function working from the box will not be enough. And thirdly, you may not be able to drive and will have to develop a mobile platform with an inferior runtime, and then it’s better to know what you are signing up for if you decide to supplement it yourself (to make sure that this is not a spherical problem in a vacuum, just try wcslen () and wcsstr () from Android NDK).
And is it just impossible to search?
The fact is that the obvious way, which formulates everything as “take and search”, is by no means the most effective, but for such a low-level and relatively part-called function, this is important. So, the plan is:
- Problem Statement: here are the definitions and conventions.
- The solution "in the forehead": it will be described here how to do it is not necessary and why.
- Z-function: the simplest version of the correct implementation of the search for substrings.
- Knuth-Morris-Pratt algorithm: another version of the correct search.
- Other search tasks: briefly run through them without a detailed description.
Formulation of the problem
The canonical version of the problem looks like this: we have the string A ( text ). It is necessary to check whether there is a substring X ( pattern ) in it, and if so, where it begins. That is exactly what the strstr () function does in C. In addition, you can also ask to find all the occurrences of the sample. Obviously, the problem makes sense only if X is not longer than A.
For simplicity, further explanation will introduce a couple of concepts at once. What a string everyone probably understands is a sequence of characters, perhaps an empty one. Symbols , or letters, belong to a certain set, which is called the alphabet (this alphabet, generally speaking, may not have anything in common with the alphabet in the everyday sense). Line length | A | - this is obviously the number of characters in it. The prefix of the string A [ ..i ] is a string of i first characters of the string A. The string suffix A [ j .. ] is the string from | A | -j + 1 last characters. The substring from A will be denoted as A [ i..j ] , and A [ i ] - the i-th character of the string. Question about empty suffixes and prefixes, etc. do not touch - it is not difficult to deal with them in place. There is also such a thing as seninel , a unique symbol not found in the alphabet. It is denoted by the $ symbol and complements the allowable alphabet with such a symbol (this is in theory, in practice it is easier to apply additional checks than to invent such a symbol that could not appear in the input strings).
In the calculations we will count the characters in the string from the first position. Code writing is traditionally easier to count from zero. The transition from one to another is not difficult.
')
Head to Head Solution
Direct search, or, as it is often said, “just take and search” is the first solution that comes to the mind of an inexperienced programmer. The point is simple: follow the tested string A and look for the occurrence of the first character of the search string X in it . When we find, we make a hypothesis that this is the very desired entry. It then remains to check in turn all subsequent characters of the pattern for matching with the corresponding characters of string A. If they all matched, then here it is, right in front of us. But if any of the characters did not match, then nothing remains but to recognize our hypothesis as incorrect, which brings us back to the character following the occurrence of the first character from X.
Many people are mistaken at this point, considering that they should not go back, but it is possible to continue processing line A from the current position. Why it is not so easy to demonstrate by the example of the search X = "AAAB" in A = "AAAAB" . The first hypothesis will lead us to the fourth symbol A : "AAAAB" , where we will find a discrepancy. If you do not roll back, then the entry, we will not find, although it is.
Incorrect hypotheses are inevitable, and due to such rollbacks under bad circumstances, it may turn out that we checked every character in A about | X | time. That is, the computational complexity is the complexity of the algorithm O (| X || A |). So the search for a phrase in a paragraph may be delayed ...
To be fair, it should be noted that if the lines are small, then such an algorithm can work faster than the “correct” algorithms at the expense of a more predictable processor behavior.
Z-function
One of the categories of correct ways to search for a string is reduced to calculating in some sense the correlation of two strings. First, we note that the task of comparing two lines began is simple and clear: we compare the corresponding letters until we find a discrepancy or one of the lines ends. Consider the set of all suffixes of the string A : A [ | A | .. ] A [ | A | -1 .. ] , ... A [ 1 .. ] . We will compare the beginning of the string itself with each of its suffixes. Comparison can reach the end of the suffix, or break on some character due to a mismatch. The length of the matched part is called the component of the Z-function for a given suffix.
That is, a Z-function is a vector of lengths of the greatest common prefix of a string with its suffix. Wow! An excellent phrase when you need to confuse or assert oneself, but to understand what it is, it is better to look at an example.
The original string is "ababcaba" . By comparing each suffix with the line itself, we get a label for the Z-function:
| suffix | line | Z | |
|---|---|---|---|
| ababcaba | ababcaba | -> | eight |
| babcaba | ababcaba | -> | 0 |
| abcaba | ababcaba | -> | 2 |
| bcaba | ababcaba | -> | 0 |
| caba | ababcaba | -> | 0 |
| aba | ababcaba | -> | 3 |
| ba | ababcaba | -> | 0 |
| a | ababcaba | -> | one |
The suffix prefix is nothing more than a substring, and the Z-function is the length of the substrings that occur simultaneously in the beginning and in the middle. Considering all the values of the components of the Z-function, you can notice some regularities. First, it is obvious that the value of the Z-function does not exceed the length of the string and coincides with it only for the “full” suffix A [ 1 .. ] (and therefore this value does not interest us - we will omit it in our reasoning). Secondly, if there is a single character in the string, it can only match itself, which means it divides the line into two parts, and the value of the Z-function can never exceed the length of the shorter part.
It is proposed to use these observations as follows. Suppose in the line "ababcabacacab" we want to search for "abca" . We take these lines and concatenate, inserting the Sentinel between them: “abca $ ababcabacacab” . The vector of the Z-function looks like this:
| a b c a $ a b a b c a b with a c a b |
| 17 0 0 1 0 2 0 4 0 0 4 0 0 1 0 2 0 |
If we discard the value for the full suffix, then the presence of the centinela limits Z i to the length of the desired fragment (it is the smaller half of the line in the sense of the problem). But if this maximum is reached, it is only in the positions of the substring entry. In our example, the quadruples mark all the positions of the occurrence of the search string (note that the found plots are located overlapping with each other, but all the same, our reasoning remains true).
Well, that means if we can quickly build a vector of the Z-function, then a search with it for all occurrences of a string is reduced to finding the value of its length in it. That's just if you calculate the Z-function for each suffix, then it will be clearly not faster than the solution "in the forehead." It helps us that the value of the next element of the vector can be found based on the previous elements.
Suppose we somehow calculated the values of the Z-function up to the corresponding i-1st symbol. Consider a certain position r <i, where we already know Z r .
So Z r characters from this position are exactly the same as at the beginning of the line. They form the so-called Z-block. We will be interested in the rightmost Z-block, that is, the one who ends the farthest (the very first does not count). In some cases, the rightmost block may be zero length (when none of the non-empty blocks cover i-1, then the rightmost one will be i-1st, even if Z i-1 = 0).

When we consider the subsequent characters inside this Z-box, it makes no sense to compare the next suffix from the very beginning, since part of this suffix has already been encountered at the beginning of the line, which means it has already been processed. It will be possible to immediately skip the characters right up to the end of the Z-block.


Namely, if we consider the i-th character in the Zr-block, that is, the corresponding character at the beginning of the line at position k = i-r + 1. The function Z k is already known. If it is less than the distance Z r - (ir) remaining to the end of the Z-block, then we can immediately be sure that the whole area of coincidence for this symbol lies inside the r-block of the Z-block and the result will be the same as in the beginning of the line: Z i = Z k . If Z k > = Z r - (ir), then Z i is also greater than or equal to Z r - (ir). To find out how much more it is, we will need to check the symbols following the Z-block. Moreover, in case of coincidence of these characters with the corresponding at the beginning of the line, Z i is increased by h: Z i = Z k + h. As a result, we may have a new right-most Z-block (if h> 0).

Thus, we have to compare characters only to the right of the rightmost Z-block, and due to successful comparisons, the block “moves” to the right, and unsuccessful ones report that the calculation for this position is over. This provides us with the construction of the entire vector of the Z-function in a time linear in the line length.
Applying this algorithm to search for substrings we obtain the complexity of the time O (| A | + | X |), which is much better than the product, which was in the first version. True, we had to store the vector for the Z-function, which would take additional memory of order O (| A | + | X |). In fact, if you do not need to find all occurrences, but only one is enough, then you can get by with O (| X |) memory, since the length of the Z-block still cannot be more than | X |, except that you can not continue processing the string after the first occurrence.
Finally, an example of a function that calculates the Z-function. Just a model option without any tricks.
void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } }
void z_preprocess(vector<int> & Z, const string & str) { const size_t len = str.size(); Z.clear(); Z.resize(len); if (0 == len) return; Z[0] = len; for (size_t curr = 1, left = 0, right = 1; curr < len; ++curr) { if (curr >= right) { size_t off = 0; while ( curr + off < len && str[curr + off] == str[off] ) ++off; Z[curr] = off; right = curr + Z[curr]; left = curr; } else { const size_t equiv = curr - left; if (Z[equiv] < right - curr) Z[curr] = Z[equiv]; else { size_t off = 0; while ( right + off < len && str[right - curr + off] == str[right + off] ) ++off; Z[curr] = right - curr + off; right += off; left = curr; } } } }
Knuth-Morris-Pratt Algorithm (CMP)
Despite the logical simplicity of the previous method, a more popular is another algorithm, which in some sense is the inverse of the Z-function - the Knut-Morris-Pratt algorithm (CMP). We introduce the concept of prefix function . The prefix function for the i-th position is the length of the maximum string prefix, which is shorter than i and which matches the suffix of the prefix of length i. If the definition of the Z-function didn’t hit the opponent outright, then with this combo you will definitely be able to put it in place :) And in human language it looks like this: take every possible string prefix and look at the longest match beginning with the end of the prefix (disregarding the trivial match with myself). Here is an example for ababcaba :
| prefix | prefix | p |
|---|---|---|
| a | a | 0 |
| ab | ab | 0 |
| ab a | a ba | one |
| ab ab | ab ab | 2 |
| ababc | ababc | 0 |
| ababc a | a babca | one |
| ababc ab | ab abcab | 2 |
| ababc aba | aba bcaba | 3 |
Again, we observe a number of properties of the prefix function. First, the values are bounded above by their number, which follows directly from the definition - the prefix length must be greater than the prefix function. Secondly, the unique symbol in the same way divides the string into two parts and limits the maximum value of the prefix-function to the length of the smaller part - because everything that is longer will contain a unique, nothing else equal symbol.
From here we get the conclusion that interests us. Suppose we did reach at some element of this theoretical ceiling. This means that such a prefix has ended here, that the initial part coincides with the final part and one of them represents the “complete” half. It is clear that in the prefix the complete half should be in front, which means with this assumption it should be the shorter half, the maximum we reach on the longer half.
Thus, if, as in the previous part, we concatenate the desired line with the one in which we are looking through the Sentinel, then the point of entry of the length of the required substring in the component of the prefix function will correspond to the place where the entry ends. Take our example: in the string “ababcabacacab” we are looking for “abca” . The concatenated version of abca $ ababcabacacab . The prefix function looks like this:
| a b c a $ a b a b c a b with a c a b |
| 0 0 0 1 0 1 2 1 2 3 2 2 3 4 0 1 2 |
Again, we found all occurrences of the substring in one fell swoop - they end in four positions. It remains to understand how to effectively calculate this prefix function. The idea of the algorithm is slightly different from the idea of constructing a Z-function.

The very first value of the prefix function is obviously 0. Suppose we calculated the prefix function to the i-th position inclusive. Consider the i + 1st character. If the value of the prefix function in the i-th position is P i , then the prefix A [ ..P i ] coincides with the substring A [ iP i + 1..i ] . If the symbol A [ P i +1 ] coincides with A [ i + 1 ] , then we can safely write down that Pi + 1 = Pi + 1. But if not, then the value can be either less or the same. Of course, when P i = 0 there is no place to decrease much, so in this case P i + 1 = 0. Suppose that P i > 0. Then there is the prefix A [ ..P i ] in the string, which is equivalent to the substring A [ iP i + 1..i ] . The desired prefix function is formed within these equivalent sections plus the character being processed, which means we can forget about the entire line after the prefix and leave only the given prefix and i + 1st character - the situation will be identical.

The task at this step has been reduced to a task for a line with a cut out center line: A [ ..P i ] A [ i + 1 ] , which can be solved recursively in the same way (although tail recursion is not a recursion at all, but a cycle). That is, if A [ P P i +1 ] coincides with A [ i + 1 ] , then P i + 1 = P P i +1, otherwise, we again throw out part of the line from consideration, etc. Repeat the procedure until we find a match or do not reach 0.

The repetition of these operations should be alerted - it would seem that there are two nested cycles. But it is not. The fact is that a nested loop with a length of k iterations reduces the prefix function in the i + 1 position by at least k-1, and in order to increase the prefix function to such a value, you need at least k-1 times successfully match the letters by processing k-1 characters. That is, the cycle length corresponds to the interval between the execution of such cycles and therefore the complexity of the algorithm is still linear in the length of the processed line. With memory, this is the same situation as with the Z-function - linear in the length of the line, but there is a way to save. In addition, there is a convenient fact that the characters are processed sequentially, that is, we are not obliged to process the entire line if we have already received the first entry.
Well, for example, a snippet of code:
void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } }
void calc_prefix_function(vector<int> & prefix_func, const string & str) { const size_t str_length = str.size(); prefix_func.clear(); prefix_func.resize(str_length); if (0 == str_length) return; prefix_func[0] = 0; for (size_t current = 1; current < str_length; ++current) { size_t matched_prefix = current - 1; size_t candidate = prefix_func[matched_prefix]; while (candidate != 0 && str[current] != str[candidate]) { matched_prefix = prefix_func[matched_prefix] - 1; candidate = prefix_func[matched_prefix]; } if (candidate == 0) prefix_func[current] = str[current] == str[0] ? 1 : 0; else prefix_func[current] = candidate + 1; } }
Despite the fact that the algorithm is more intricate, its implementation is even simpler than for the Z-function.
Other Search Tasks
Then there will be just a lot of letters that do not limit the search tasks to strings and that there are other tasks and other solutions, so if anyone is not interested, then you can not read further. This information is just for reference, in case of need, at least to realize that “everything is already stolen before us” and not reinvent the bicycle.
Although the above algorithms guarantee linear execution time, the title of the “default algorithm ” was given to the Boyer-Moore algorithm . On average, it also gives linear time, but also has a better constant for this linear function, but that is on average. There are “bad” data on which he is no better than the simplest “head-on” comparison (well, just like with qsort). It is extremely confused and will not be considered - all the same I do not remember. There are a number of exotic algorithms that are focused on natural language processing and rely in their optimizations on the statistical properties of words in a language.
Well, well, we have an algorithm that somehow or another O (| X | + | A |) is looking for a substring in the string. Now imagine that we are writing a guest book engine. We have a list of forbidden swear words (it is clear that this will not help, but the task is just for example). We are going to filter messages. We will look for each of the forbidden words in the message and ... this will take O (| X 1 | + | X 2 | + ... + | X n | + n | A |). Somehow so-so, especially if the dictionary of "mighty expressions" of "great and mighty" is very "mighty." For this case, there is a way to pre-process the dictionary of the required strings, that the search will occupy only O (| X 1 | + | X 2 | + ... + | X n | + | A |), and this can be significantly less, especially if the messages are long.
Such preprocessing is reduced to building a boron (trie) from a dictionary: a tree starts at some fictitious root, nodes correspond to letters of words in a dictionary, the depth of a tree node corresponds to the number of a letter in a word. The nodes where the word from the dictionary ends is called terminal and is labeled in some way (in red in the figure).

The resulting tree is an analogue of the prefix function of the CMP algorithm. With it, you can find all occurrences of all vocabulary words in a phrase. It is necessary to go through the tree, checking for the presence of the next symbol in the form of a tree node, simultaneously noting the encountered terminal vertices - these are occurrences of words. If there is no corresponding node in the tree, then, like in the ILC, a rollback takes place higher up the tree using special links. This algorithm is called the Aho-Corasica algorithm . The same scheme can be used to search during input and prediction of the next character in electronic dictionaries.
In this example, the construction of boron is simple: we simply add words to the boron in turn (nuances only with additional references for “kickbacks”). There are a number of optimizations aimed at reducing the memory use of this tree (the so-called boron compression - skipping sections without branching). In practice, these optimizations are almost optional. The disadvantage of this algorithm is its alphabet dependence: the time to process the node and the memory occupied depends on the number of potential children, which is equal to the size of the alphabet. For large alphabets, this is a serious problem (imagine a set of Unicode characters?). You can read more about all this in this habratopic or using GoogleIndex - the benefit of information on this subject is a lot.
Now look at another task. If in the previous one we knew in advance what we would have to find in the incoming data later, here it is exactly the opposite: we were given a line in advance, in which we would be searched, but what they would be looking for was unknown, but they would be searched a lot. A typical example is a search engine. The document in which the word is searched is known in advance, but the words that are searched there, are strewn on the go. The question is, again, how instead of O (| X 1 | + | X 2 | + ... + | X n | + n | A |) get O (| X 1 | + | X 2 | + ... + | X n | + | A |)?
It is proposed to build a bur in which will be all possible suffixes of the existing string. Then the search for a pattern will be reduced to checking the presence of a path in the tree corresponding to the desired pattern. If you build such a forest by searching all the suffixes, then this procedure can take O (| A | 2 ) time, and there is a lot of memory. But, fortunately, there are algorithms that allow you to build such a tree at once in a compressed form - a suffix tree , and to do it in O (| A |). Recently on Habré was about this article , so that those interested can read about the algorithm Ukkonen there.
Poorly in a suffix tree, as usual, there are two things: the fact that it is a tree and the fact that the nodes of the tree are alphabetically dependent. The suffix array is spared from these shortcomings. The essence of the suffix array is that if all the suffixes of the string are sorted, then the search for the substring will be reduced to the search for a group of adjacent suffixes by the first letter of the desired pattern and further refinement of the range by the subsequent ones. At the same time, there is no need to keep the suffixes in sorted form, it is enough to store the positions in which they begin in the original data. True, the time dependences of this structure are somewhat worse: a single search will do O (| X | + log | A |) if you think and do everything neatly, and O (| X | log | A |) if you do not bother. For comparison, in a tree for a fixed alphabet O (| X |). But the fact that this is an array, and not a tree, can improve the situation with memory caching and make it easier for the predictor of processor transitions. A suffix array is built in linear time using the Kärkkäinen-Sanders algorithm (sorry, but I have no idea how it should sound in Russian). Today it is one of the most popular methods of indexing strings.
We will not touch on the issues of approximate search for strings and analysis of the degree of similarity here - it is too big an area to be stuffed into this article. Just to mention that people there did not eat bread for nothing, and came up with many different approaches, so if you run into a similar task, find and read. Quite possibly this problem has already been solved.
Thanks to those who read! And for those who read to here, thank you very much!
UPD: Added a link to the informative article about boron (it’s a ray, it’s a prefix tree, it’s a loaded tree, it’s a trie).
Source: https://habr.com/ru/post/113266/
All Articles