Recently, Habré has appeared, and there are also many informative articles describing the work and principle of the concept of “neural network”, but, unfortunately, as always, very little description and analysis of the practical results obtained or not received. I think that many, like me, are more comfortable, easier and clearer to understand with a real example. Therefore, in this article I will try to describe an almost step by step solution to the problem of recognizing the letters of the Latin alphabet + an example for independent research. Recognition of numbers using a single-layer perceptron has already been done, now let's look at it and teach the computer to recognize letters.

Our problem

In short, I will say that neural networks in general make it possible to solve a very large range of practical problems, in particular, recognition problems. In most cases, the latter have a "template" character. For example, a system that “reads” bank checks, by efficiency, is several times greater than the operator. In the tasks of such a plan, the use of neural networks is justified and largely saves money and resources.

We will determine what we need to disassemble, understand and do. We need to build an expert system that can recognize the letters of the Latin alphabet. To do this, you need to understand the capabilities of neural networks (NA) and build a system that can recognize the letters of the Latin alphabet. In detail with the theory of neural networks can be found at the links given at the end of the article. This article does not find descriptions of the theory (mathematics) of the work of the National Assembly or the descriptions of the commands when working with MATLAB (well, only if the links are at the end of the article), this remains on your conscience. The purpose of the article is to show and tell the application of a neural network for a practical task, show results, run into pitfalls, try to show that it is possible to squeeze out of a neural network, without going into details how it is implemented, for the rest there is specialized literature, from which everything don't run anyway.

Let's try to figure out the possibilities when using a neural network with back propagation of an error in order to recognize the letters of the Latin alphabet. We will implement the algorithm in the software environment of the MATLAB engineering math package, namely, the power of the Neural Network Toolbox will be needed.

What is given

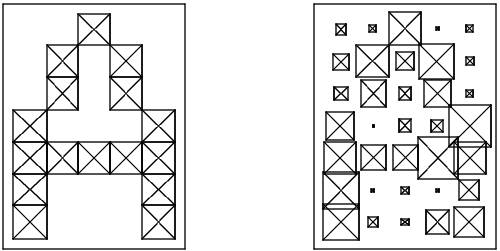
It is necessary to understand the input data. We all imagine what the letters represent, how they look on the monitor in a book, etc. (as, for example, presented in the figure below).



In reality, it is often necessary to work not with ideal letters, as shown above, but more often as shown below, that is, distortions are introduced in the symbols.



Now back to the problem of image representation, understandable to the neural network. It is clear that each letter in the image can be represented as a matrix with certain values ​​of elements that can clearly define the letter. That is, it is convenient to formalize the representation of the Latin alphabet character by a matrix of n rows and m columns. Each element of such a matrix can take values ​​in the range [0, 1]. Thus, the symbol A in such a formalized form will look as follows (on the left - without distortion, on the right - with distortion):



Not many imagining what is happening in my head, let's proceed to implement it in MATLAB. In this package, the Latin alphabet is already provided, there is even a demo example of working with it, but we will take only the alphabet from it. Therefore, you can use their data, and you can even draw all the letters yourself, it is optional.

MATLAB offers characters that are formalized by a matrix of 7 rows and 5 columns. But such a matrix cannot be simply fed to the input of a neural network, for this it is necessary to collect a 35 - element vector.

For compatibility with different versions and convenience, I saved the matrix of characters in the file (and so you can use the function prprob, it will load the alphabet into the workspace).

It is known from theory that we need input data and output data (targets, target data) for network training. The target vector will contain 26 elements, where one of the elements has the value 1, and all other elements are equal to 0, the element number containing the unit encodes the corresponding letter of the alphabet.

To summarize, the input 35-element vector is fed to the input of the neural network, which is mapped to the corresponding letter from the 26-element output vector. The output of the NA is the 26-element vector, in which only one element that encodes the corresponding letter of the alphabet is 1. Having dealt with the creation of the interface for working with the NA, we will proceed to its creation.

Network building

We construct a neural network that includes 35 inputs (because the vector consists of 35 elements) and 26 outputs (because 26 letters). This NS is a two-layer network. The activation function will put the logarithmic sigmoid function, which is convenient to use, because the output vectors contain elements with values ​​in the range from 0 to 1, which is then conveniently transferred to Boolean algebra. On the hidden level, select 10 neurons (because just like that, you can any value, then check, and how many they need). If something is not clear to you from the above written about the construction of the network, please read about it in the literature (necessary concepts if you are going to work with the National Assembly). Schematically considered network can be represented by the following scheme:



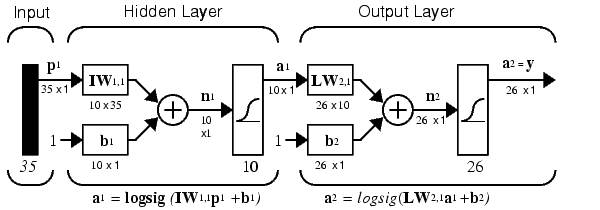
And if this is all written in the syntax of the MATLAB scripting language, we get:

1. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
2. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
3. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
4. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
5. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
6. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
7. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
8. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );
9. S1 = 10; % [S2,Q] = size(targets); % ( ) P = alphabet; % , % net = newff(minmax(P), % [S1 S2], % {'logsig' 'logsig'}, % 'traingdx' % ( ) );

')

Network training

Now that the NA has been created, it is necessary to teach her, because she, as a small child, knows nothing, a completely blank sheet. The neural network is trained using the back propagation procedure - propagation of error signals from the outputs of the NA to its inputs, in the direction opposite to the direct propagation of signals in normal operation (there are also learning methods, this is considered the most basic, and all the others are modifications).

To create a neural network that can work with noisy input data, it is necessary to train the network by applying data to the input, both with noise and without it. To do this, you must first train the network, submitting data without a noise component. Then, when we train the network on ideal data, we will conduct training on sets of ideal and noisy input data (as we will see later, this is very important, because such training increases the percentage of correct letter recognition).

For all workouts, the traingdx function is used — a network training function that modifies the values ​​of weights and displacements according to the gradient descent method taking into account the moments and using adaptive training.

First, you need to train the network on non-noisy data, that is, starting with simple. In principle, the order of training is not particularly important, but often changing the order, you can get a different quality of the adequacy of the National Assembly. Then, in order to be able to make a neural system that is not sensitive to noise, we will train the network with two perfect copies and two copies containing noise (noise with dispersion of 0.1 and 0.2 is added). The target value will therefore contain 4 copies of the target vector.

After completing the training with noisy input data, it is necessary to repeat the training with ideal input data in order for the neural network to successfully cope with the ideal input data. I don’t cite pieces of code, because they are very simple, using one train function, which is easy to use.

Network testing

The most interesting and significant stage is what we got. For this, I will provide dependency graphs with comments.

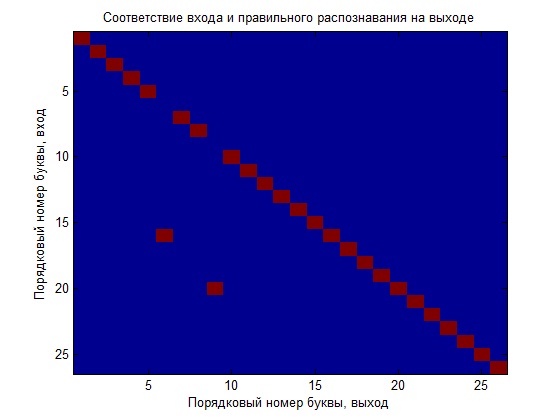
First, we trained the network only on ideal data and now we will see how it copes with recognition. For clarity, I will build a graph illustrating the input output ratio, that is, the number of the letter at the input must correspond to the number of the letter at the output (the perfect recognition will be the case when we get the diagonal of the quadrant on the graph).



As you can see, the network has coped poorly with the task, you can of course play around with the training parameters (which is desirable to do) and this will give the best result, but we will make another comparison, create a new network and train it with noisy data, and then compare the obtained NN.

Now back to the question, but how many neurons in the hidden layer should be. To do this, we construct a dependency that graphically shows the ratio of neurons in the hidden layer and the percentage of erroneous recognition.



As can be seen, with an increase in the number of neurons, 100% recognition of input data can be achieved. Also increasing the likelihood of correct recognition will be re-training the wound of a trained neural network with a large amount of data. After such a stage it is easy to see that the percentage of correct letter recognition increases. True, everything works well up to a certain point, because it can be seen that when the number exceeds 25 neurons, the network starts to make mistakes.



Remember that we are going to train another network, using in addition to the ideal data, also noisy data and compare. So let's take a look at which network is better, based on the results obtained in the graph below.



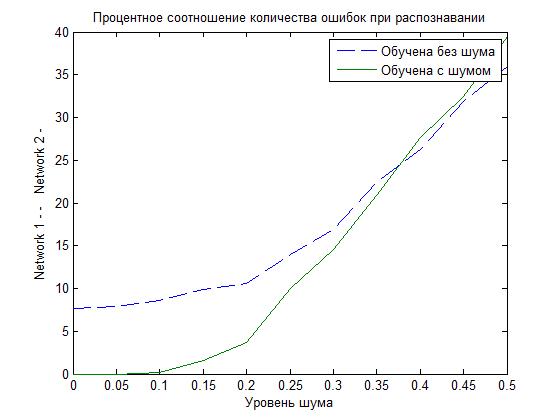
As it can be seen, with not significant noise, the NA, which was trained by the distorted data, does much better (the percentage of erroneous recognition is lower).

Summarizing

I tried not to torment with details and trifles, I tried to organize a "murzilka" (a magazine with pictures) in order to simply understand what the use of NA is.

As for the obtained results, they indicate that in order to increase the number of correct recognition, it is necessary to train (train) the neural network more and increase the number of neurons in the hidden layer. If it is possible, then increase the resolution of the input vectors, for example, the letter is formalized by a 10x14 matrix. The most important thing is that in the learning process it is necessary to use a larger number of input data sets, with as much noise as possible with useful information.

Below is an example in which everything has been done, all that is described and cited in the article (even a little more). I tried to tell something useful and not to load with some incomprehensible formulas. More articles are planned, but it all depends on your wishes.

Example and literature

CharacterRecognition.zip

Selection of articles on neural networks

Description of neural network algorithms