Dynamic programming. Classic tasks
Hello, Habrahabr. At the moment I am working on a tutorial on Olympiad programming, one of the paragraphs of which is devoted to dynamic programming. The following is an excerpt from this paragraph. Trying to explain this topic as simply as possible, I tried to accompany the difficult moments with illustrations. I am interested in your opinion on how understandable this material has turned out. Also I will be glad to advice what other tasks should be included in this section.
In many programming olympiad problems, solving using recursion or full enumeration requires performing a very large number of operations. Attempting to solve such problems, for example, by exhaustive search, leads to exceeding the execution time.
However, among the enumerated and some other tasks, we can distinguish a class of problems that have one good property: having solutions of some subtasks (for example, for a smaller number n ), one can find the solution to the original problem almost without searching.
')
Such tasks are solved by dynamic programming, and dynamic programming itself means reducing a task to subtasks.
The classic task on the sequence is the following.
The Fibonacci sequence F n is given by the formulas: F 1 = 1, F 2 = 1,
F n = F n - 1 + F n - 2 for n > 1. It is necessary to find F n by the number n .
One solution that may seem logical and effective is to solve using recursion:
Using such a function, we will solve the problem “from the end” - we will decrease n step by step until we reach the known values.
But as you can see, such a seemingly simple program already with n = 40 runs noticeably for a long time. This is due to the fact that the same intermediate data are calculated several times - the number of operations grows at the same rate as the Fibonacci numbers grow exponentially.
One of the ways out of this situation is to save the intermediate results already found for the purpose of their reuse:
The above solution is correct and effective. But for this problem a simpler solution is applicable:
Such a solution can be called a solution "from the beginning" - we first fill in the known values, then we find the first unknown value ( F 3 ), then the next one, etc., until we reach the desired one.
It is this solution that is classical for dynamic programming: we first solved all the subtasks (found all F i for i < n ), then, knowing the solutions of the subtasks, we found the answer ( F n = F n - 1 + F n - 2 , F n - 1 and F n - 2 have already been found).
To better understand the essence of dynamic programming, we first define the concepts of tasks and subtasks more formally.
Let the original problem be to find some number T with the initial data n 1 , n 2 , ..., n k . That is, we can talk about the function T ( n 1 , n 2 , ..., n k ), the value of which is the answer we need. Then we will consider tasks as subtasks.
T ( i 1 , i 2 , ..., i k ) for i 1 < n 1 , i 2 < n 2 , ..., i k < n k .
Further we will talk about one-dimensional, two-dimensional and multidimensional dynamic programming with k = 1, k = 2, k > 2, respectively.
The following problem of one-dimensional dynamic programming is found in various variations.
Task 1. Calculate the number of sequences of zeros and units of length n in which two consecutive units are not found.
For n <32, a full search will take several seconds, and for n = 64, a full search will not be possible in principle. To solve the problem using dynamic programming, we reduce the original problem to subtasks.
When n = 1, n = 2, the answer is obvious. Suppose that we have already found K n - 1 , K n - 2 - the number of such sequences of length n - 1 and n - 2.
Let us see what a sequence of length n can be. If its last character is 0, then the first n - 1 is any valid sequence of length.
n - 1 (it doesn't matter if it ends with zero or one — 0 goes next). Such sequences of all K n - 1 . If the last character is 1, then the penultimate character must be equal to 0 (otherwise there will be two units in a row), and the first
n - 2 characters - any correct sequence of length n - 2, the number of such sequences is equal to K n - 2 .

Thus, K 1 = 2, K 2 = 3, K n = K n - 1 + K n - 2 for n > 2. That is, this task actually boils down to finding Fibonacci numbers.
The classical problem of two-dimensional dynamic programming is the problem of routes on a rectangular field.
In different formulations, it is necessary to count the number of routes or find a route that is the best in a sense.
We give a couple of formulations of such problems:
Task 2. Given a rectangular field of size n * m cells. You can make steps a single cell to the right or down. Calculate how many ways you can get from the left upper cell to the lower right one.
Task 3. Given a rectangular field of size n * m cells. You can make steps a single cell to the right, down or diagonally to the right down. Each cell contains a certain natural number. It is necessary to get from the upper left cell to the right lower one. The route weight is calculated as the sum of the numbers from all the visited cells. It is necessary to find a route with a minimum weight.
For all such tasks, it is characteristic that each individual route cannot pass two or more times in the same cell.
Let us consider problem 2 in more detail. In a certain cell with coordinates ( i , j ) one can come only from above or from the left, that is, from cells with coordinates ( i - 1, j ) and ( i , j - 1):

Thus, for the cell ( i , j ) the number of routes A [i] [j] will be equal to
A [i - 1] [j] + A [i] [j - 1], that is, the task is reduced to two subtasks. In this implementation, two parameters are used - i and j - therefore, with reference to this task, we are talking about two-dimensional dynamic programming.
Now we can go sequentially through the rows (or columns) of the array A, finding the number of routes for the current cell using the above formula. You must first put the number 1 in A [0] [0].
In task 3, we can get into the cell with coordinates ( i , j ) from the cells with coordinates
( i - 1, j), ( i , j - 1) and ( i - 1, j - 1). Suppose that for each of these three cells we have already found the route of the minimum weight, and weights were placed in W [i - 1] [j], W [i] [j - 1],
W [i - 1] [j - 1]. To find the minimum weight for ( i , j ), you must select the minimum of the weights W [i - 1] [j], W [i] [j - 1], W [i - 1] [j - 1] and add to there is a number written in the current cell:
W [i] [j] = min (W [i – 1] [j], W [i] [j - 1], W [i - 1] [j - 1]) + A [i] [j] ;
This task is complicated by the fact that it is necessary to find not only the minimum weight, but also the route itself. Therefore, in addition to each cell, we will write to another array, from which side we should get into it.
The following figure shows an example of the source data and one of the steps of the algorithm.
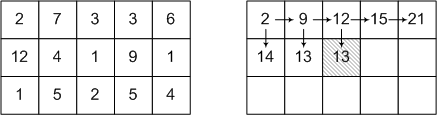
In each of the already passed cells exactly one arrow leads. This arrow shows which side needs to come into this cell in order to get the minimum weight recorded in the cell.
After passing through the entire array, it will be necessary to trace the route itself from the last cell, following the arrows in the opposite direction.
Consider the problem of increasing subsequence.
Task 4. Given a sequence of integers. It is necessary to find its longest strictly increasing subsequence.
Let's start solving the problem from the beginning - we will look for the answer, starting with the first members of this sequence. For each number i, we will look for the largest ascending subsequence ending with an element in position i . Let the original sequence be stored in array A. In the array L, we write the lengths of the maximal subsequences ending in the current element. Let we find all L [i] for 1 <= i <= k - 1. Now we can find L [k] as follows. We look through all elements A [i] for 1 <= i < k - 1. If
A [i] <A [k], then the k -th element can be a continuation of a subsequence terminated by the element A [i]. The length of the obtained subsequence will be 1 greater than L [i]. To find L [k], you need to iterate through all i from 1 to k - 1:
L [k] = max (L [i]) + 1, where the maximum is taken over all i such that A [i] <A [k] and
1 <= i < k .
Here, the maximum of the empty set will be considered equal to 0. In this case, the current element will be the only one in the selected sequence, and will not be a continuation of one of the previous ones. After filling the array L, the length of the largest increasing subsequence will be equal to the maximum element L.
To restore the subsequence itself, you can also save the number of the previous selected element for each element, for example, in the array N.
Consider the solution of this problem on the example of the sequence 2, 8, 5, 9, 12, 6. Since up to 2 there is not a single element, the maximum subsequence contains only one element - L [1] = 1, and there is not one before it - N [1] = 0. Next,
2 <8, so 8 can be a continuation of the sequence with the previous element. Then L [2] = 2, N [2] = 1.
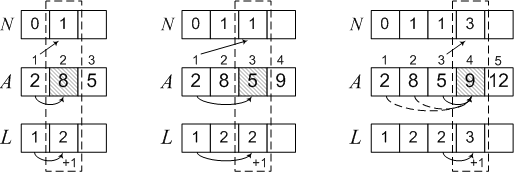
Less than A [3] = 5, only the element A [1] = 2, so 5 can be the continuation of only one subsequence - the one that contains 2. Then
L [3] = L [1] + 1 = 2, N [3] = 1, since 2 is in position number 1. Similarly, we perform three more steps of the algorithm and get the final result.
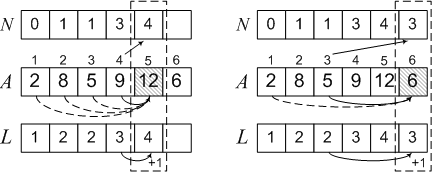
Now choose the maximum element in the array L and restore the subsequence 2, 5, 9, 12 by the array N.
Another classic dynamic programming problem is the palindrome task.
Task 5. Given a string of capital letters of the Latin alphabet. It is necessary to find the length of the longest palindrome, which can be obtained by crossing out some letters from this string.
Denote this string by S, and its characters by S [i], 1 <= i <= n . We will consider the possible substrings of this string from the i -th to jth character, denote them by S ( i , j ). The lengths of the maximum palindromes for substrings will be written into a square array L: L [i] [j] - the length of the maximum palindrome, which can be obtained from the substring S ( i , j ).
Let's start solving the problem with the simplest substrings. For a string of one character (that is, substrings of the form S ( i , i )), the answer is obvious - no need to cross out anything, such a string will be a palindrome. For a string of two characters S ( i , i + 1), two options are possible: if the characters are equal, then we have a palindrome, nothing needs to be crossed out. If the characters are not equal, then delete any.
Suppose now that we are given a substring S ( i , j ). If the first (S [i]) and last (S [j]) characters of the substring do not match, then one of them just needs to be crossed out. Then we will have a substring of S ( i , j - 1) or S ( i + 1, j ) - that is, we will reduce the task to a subtask: L [i] [j] = max (L [i] [j - 1] , L [i + 1] [j]). If the first and last symbols are equal, then we can leave both, but it is necessary to know the solution to the problem S ( i + 1, j - 1):
L [i] [j] = L [i + 1] [j - 1] + 2.
Consider the decision on the example of the string ABACCBA. First of all, fill in the diagonal of the array with units; they will correspond to the substrings S ( i , i ) of one character. Then we begin to consider substrings of length two. In all substrings, except S (4, 5), the characters are different, therefore, we write 1 in the corresponding cells, and 2 in L [4] [5].
It turns out that we will fill the array along the diagonals, starting with the main diagonal leading from the upper left corner to the lower right corner. For substrings of length 3, the following values are obtained: in the ABA substring, the first and last letters are equal, therefore
L [1] [3] = L [2] [2] + 2. In the remaining substrik the first and the last letters are different.
BAC: L [2] [4] = max (L [2] [3], L [3] [4]) = 1.
ACC: L [3] [5] = max (L [3] [4], L [4] [5]) = 2.
CCB: L [4] [6] = max (L [4] [5], L [5] [6]) = 2.
CBA: L [5] [7] = max (L [5] [6], L [6] [7]) = 1.
Continuing further similar reasoning, we will fill all the cells under the diagonal and in the cell L [1] [7] = 6 we will get the answer.
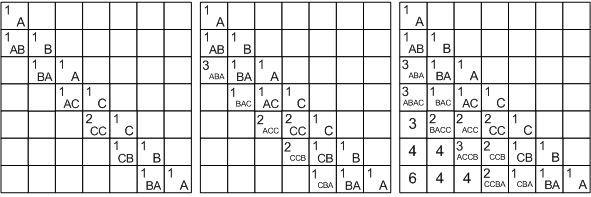
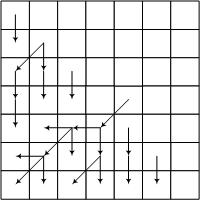
If in the task it is necessary to output not the length, but the palindrome itself, then in addition to the length array we need to build an array of transitions - for each cell, remember which of the cases was implemented (in the figure for clarity, instead of numeric values that encode the transitions, the corresponding arrows are drawn) .
In many programming olympiad problems, solving using recursion or full enumeration requires performing a very large number of operations. Attempting to solve such problems, for example, by exhaustive search, leads to exceeding the execution time.
However, among the enumerated and some other tasks, we can distinguish a class of problems that have one good property: having solutions of some subtasks (for example, for a smaller number n ), one can find the solution to the original problem almost without searching.
')
Such tasks are solved by dynamic programming, and dynamic programming itself means reducing a task to subtasks.
Sequences
The classic task on the sequence is the following.
The Fibonacci sequence F n is given by the formulas: F 1 = 1, F 2 = 1,
F n = F n - 1 + F n - 2 for n > 1. It is necessary to find F n by the number n .
One solution that may seem logical and effective is to solve using recursion:
int F (int n) {
if (n <2) return 1;
else return F (n - 1) + F (n - 2);
} Using such a function, we will solve the problem “from the end” - we will decrease n step by step until we reach the known values.
But as you can see, such a seemingly simple program already with n = 40 runs noticeably for a long time. This is due to the fact that the same intermediate data are calculated several times - the number of operations grows at the same rate as the Fibonacci numbers grow exponentially.
One of the ways out of this situation is to save the intermediate results already found for the purpose of their reuse:
int F (int n) {
if (A [n]! = -1) return A [n];
if (n <2) return 1;
else {
A [n] = F (n - 1) + F (n - 2);
return A [n];
}
}
The above solution is correct and effective. But for this problem a simpler solution is applicable:
F [0] = 1; F [1] = 1; for (i = 2; i <n; i ++) F [i] = F [i - 1] + F [i - 2];
Such a solution can be called a solution "from the beginning" - we first fill in the known values, then we find the first unknown value ( F 3 ), then the next one, etc., until we reach the desired one.
It is this solution that is classical for dynamic programming: we first solved all the subtasks (found all F i for i < n ), then, knowing the solutions of the subtasks, we found the answer ( F n = F n - 1 + F n - 2 , F n - 1 and F n - 2 have already been found).
One-dimensional dynamic programming
To better understand the essence of dynamic programming, we first define the concepts of tasks and subtasks more formally.
Let the original problem be to find some number T with the initial data n 1 , n 2 , ..., n k . That is, we can talk about the function T ( n 1 , n 2 , ..., n k ), the value of which is the answer we need. Then we will consider tasks as subtasks.
T ( i 1 , i 2 , ..., i k ) for i 1 < n 1 , i 2 < n 2 , ..., i k < n k .
Further we will talk about one-dimensional, two-dimensional and multidimensional dynamic programming with k = 1, k = 2, k > 2, respectively.
The following problem of one-dimensional dynamic programming is found in various variations.
Task 1. Calculate the number of sequences of zeros and units of length n in which two consecutive units are not found.
For n <32, a full search will take several seconds, and for n = 64, a full search will not be possible in principle. To solve the problem using dynamic programming, we reduce the original problem to subtasks.
When n = 1, n = 2, the answer is obvious. Suppose that we have already found K n - 1 , K n - 2 - the number of such sequences of length n - 1 and n - 2.
Let us see what a sequence of length n can be. If its last character is 0, then the first n - 1 is any valid sequence of length.
n - 1 (it doesn't matter if it ends with zero or one — 0 goes next). Such sequences of all K n - 1 . If the last character is 1, then the penultimate character must be equal to 0 (otherwise there will be two units in a row), and the first
n - 2 characters - any correct sequence of length n - 2, the number of such sequences is equal to K n - 2 .

Thus, K 1 = 2, K 2 = 3, K n = K n - 1 + K n - 2 for n > 2. That is, this task actually boils down to finding Fibonacci numbers.
2D dynamic programming
The classical problem of two-dimensional dynamic programming is the problem of routes on a rectangular field.
In different formulations, it is necessary to count the number of routes or find a route that is the best in a sense.
We give a couple of formulations of such problems:
Task 2. Given a rectangular field of size n * m cells. You can make steps a single cell to the right or down. Calculate how many ways you can get from the left upper cell to the lower right one.
Task 3. Given a rectangular field of size n * m cells. You can make steps a single cell to the right, down or diagonally to the right down. Each cell contains a certain natural number. It is necessary to get from the upper left cell to the right lower one. The route weight is calculated as the sum of the numbers from all the visited cells. It is necessary to find a route with a minimum weight.
For all such tasks, it is characteristic that each individual route cannot pass two or more times in the same cell.
Let us consider problem 2 in more detail. In a certain cell with coordinates ( i , j ) one can come only from above or from the left, that is, from cells with coordinates ( i - 1, j ) and ( i , j - 1):

Thus, for the cell ( i , j ) the number of routes A [i] [j] will be equal to
A [i - 1] [j] + A [i] [j - 1], that is, the task is reduced to two subtasks. In this implementation, two parameters are used - i and j - therefore, with reference to this task, we are talking about two-dimensional dynamic programming.
Now we can go sequentially through the rows (or columns) of the array A, finding the number of routes for the current cell using the above formula. You must first put the number 1 in A [0] [0].
In task 3, we can get into the cell with coordinates ( i , j ) from the cells with coordinates
( i - 1, j), ( i , j - 1) and ( i - 1, j - 1). Suppose that for each of these three cells we have already found the route of the minimum weight, and weights were placed in W [i - 1] [j], W [i] [j - 1],
W [i - 1] [j - 1]. To find the minimum weight for ( i , j ), you must select the minimum of the weights W [i - 1] [j], W [i] [j - 1], W [i - 1] [j - 1] and add to there is a number written in the current cell:
W [i] [j] = min (W [i – 1] [j], W [i] [j - 1], W [i - 1] [j - 1]) + A [i] [j] ;
This task is complicated by the fact that it is necessary to find not only the minimum weight, but also the route itself. Therefore, in addition to each cell, we will write to another array, from which side we should get into it.
The following figure shows an example of the source data and one of the steps of the algorithm.

In each of the already passed cells exactly one arrow leads. This arrow shows which side needs to come into this cell in order to get the minimum weight recorded in the cell.
After passing through the entire array, it will be necessary to trace the route itself from the last cell, following the arrows in the opposite direction.
Tasks on subsequences
Consider the problem of increasing subsequence.
Task 4. Given a sequence of integers. It is necessary to find its longest strictly increasing subsequence.
Let's start solving the problem from the beginning - we will look for the answer, starting with the first members of this sequence. For each number i, we will look for the largest ascending subsequence ending with an element in position i . Let the original sequence be stored in array A. In the array L, we write the lengths of the maximal subsequences ending in the current element. Let we find all L [i] for 1 <= i <= k - 1. Now we can find L [k] as follows. We look through all elements A [i] for 1 <= i < k - 1. If
A [i] <A [k], then the k -th element can be a continuation of a subsequence terminated by the element A [i]. The length of the obtained subsequence will be 1 greater than L [i]. To find L [k], you need to iterate through all i from 1 to k - 1:
L [k] = max (L [i]) + 1, where the maximum is taken over all i such that A [i] <A [k] and
1 <= i < k .
Here, the maximum of the empty set will be considered equal to 0. In this case, the current element will be the only one in the selected sequence, and will not be a continuation of one of the previous ones. After filling the array L, the length of the largest increasing subsequence will be equal to the maximum element L.
To restore the subsequence itself, you can also save the number of the previous selected element for each element, for example, in the array N.
Consider the solution of this problem on the example of the sequence 2, 8, 5, 9, 12, 6. Since up to 2 there is not a single element, the maximum subsequence contains only one element - L [1] = 1, and there is not one before it - N [1] = 0. Next,
2 <8, so 8 can be a continuation of the sequence with the previous element. Then L [2] = 2, N [2] = 1.

Less than A [3] = 5, only the element A [1] = 2, so 5 can be the continuation of only one subsequence - the one that contains 2. Then
L [3] = L [1] + 1 = 2, N [3] = 1, since 2 is in position number 1. Similarly, we perform three more steps of the algorithm and get the final result.

Now choose the maximum element in the array L and restore the subsequence 2, 5, 9, 12 by the array N.
Another classic dynamic programming problem is the palindrome task.
Task 5. Given a string of capital letters of the Latin alphabet. It is necessary to find the length of the longest palindrome, which can be obtained by crossing out some letters from this string.
Denote this string by S, and its characters by S [i], 1 <= i <= n . We will consider the possible substrings of this string from the i -th to jth character, denote them by S ( i , j ). The lengths of the maximum palindromes for substrings will be written into a square array L: L [i] [j] - the length of the maximum palindrome, which can be obtained from the substring S ( i , j ).
Let's start solving the problem with the simplest substrings. For a string of one character (that is, substrings of the form S ( i , i )), the answer is obvious - no need to cross out anything, such a string will be a palindrome. For a string of two characters S ( i , i + 1), two options are possible: if the characters are equal, then we have a palindrome, nothing needs to be crossed out. If the characters are not equal, then delete any.
Suppose now that we are given a substring S ( i , j ). If the first (S [i]) and last (S [j]) characters of the substring do not match, then one of them just needs to be crossed out. Then we will have a substring of S ( i , j - 1) or S ( i + 1, j ) - that is, we will reduce the task to a subtask: L [i] [j] = max (L [i] [j - 1] , L [i + 1] [j]). If the first and last symbols are equal, then we can leave both, but it is necessary to know the solution to the problem S ( i + 1, j - 1):
L [i] [j] = L [i + 1] [j - 1] + 2.
Consider the decision on the example of the string ABACCBA. First of all, fill in the diagonal of the array with units; they will correspond to the substrings S ( i , i ) of one character. Then we begin to consider substrings of length two. In all substrings, except S (4, 5), the characters are different, therefore, we write 1 in the corresponding cells, and 2 in L [4] [5].
It turns out that we will fill the array along the diagonals, starting with the main diagonal leading from the upper left corner to the lower right corner. For substrings of length 3, the following values are obtained: in the ABA substring, the first and last letters are equal, therefore
L [1] [3] = L [2] [2] + 2. In the remaining substrik the first and the last letters are different.
BAC: L [2] [4] = max (L [2] [3], L [3] [4]) = 1.
ACC: L [3] [5] = max (L [3] [4], L [4] [5]) = 2.
CCB: L [4] [6] = max (L [4] [5], L [5] [6]) = 2.
CBA: L [5] [7] = max (L [5] [6], L [6] [7]) = 1.
Continuing further similar reasoning, we will fill all the cells under the diagonal and in the cell L [1] [7] = 6 we will get the answer.

If in the task it is necessary to output not the length, but the palindrome itself, then in addition to the length array we need to build an array of transitions - for each cell, remember which of the cases was implemented (in the figure for clarity, instead of numeric values that encode the transitions, the corresponding arrows are drawn) .

Source: https://habr.com/ru/post/113108/
All Articles