Mamdani algorithm in fuzzy inference systems
Introduction
It just so happened that any article on fuzzy logic can be started from the mention of the name Lotfi Zade. And I will not be an exception. The fact is that this man became not only the founding father of a whole scientific theory, writing the fundamental work Fuzzy Sets in 1965, but also worked on various possibilities of its practical application. He described his approach in 1973 in the text “Outline of the Systems and Decision Processes” (published in IEEE Transactions on Systems). It is noteworthy that immediately after its release, one enterprising Danish company very successfully applied the principles laid down in it to improve its management system for a complex production process.
But with all the merits of L. Zadeh, the followers of this theory made an equally important contribution. For example, the English mathematician E. Mamdani (Ebrahim Mamdani). In 1975, he developed an algorithm that was proposed as a method for controlling a steam engine. The algorithm proposed by him, based on fuzzy logical inference, made it possible to avoid an excessively large amount of computation and was appreciated by experts. This algorithm is currently the most practical application in fuzzy modeling problems.
Basic definitions
Before you begin to get acquainted with the algorithm, it is important to briefly review the following definitions:
A fuzzy variable is a tuple of the form <α, X , Α >, where:
α is the name of a fuzzy variable;
X is its domain;
A is a fuzzy set in the universe X.
')
Example: Fuzzy variable <“Heavy body armor”, { x | 0 kg < x <35 kg}, B = { x , μ ( x )}> characterizes the mass of the military body armor. We consider it heavy if its mass is> 16 kg (Fig. 1).
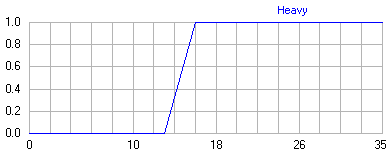
Fig. 1. Graph of the membership function μ ( x ) for a fuzzy set B
The linguistic variable is a tuple <β, T, X, G, M >, where:
β is the name of a linguistic variable;
T is the set of its values (terms);
X - the universe of fuzzy variables;
G - syntactic procedure for the formation of new terms;
M is a semantic procedure that forms fuzzy sets for each term of a given linguistic variable.
Example: Suppose we have a subjective assessment of the mass of the body armor. For example, it can be obtained from military personnel (acting as experts) who directly deal with such ammunition. This assessment can be formalized using the following linguistic variable <β, T, X, G, M > (Fig. 2), where:
β - body armor;
T - {“Lightweight bullet-proof vest (Light)”, “Bullet-proof vest of medium weight (Medium)”, “Heavy bulletproof vest (Heavy)”};
X = [0; 35];
G - procedure for the formation of new terms with the help of logical connectives and modifiers. For example, “very heavy body armor”;
M - the procedure for setting the universe X = [0; 35] of the linguistic variable values, i.e. terms from the set T.
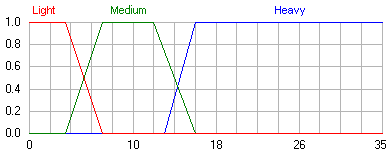
Fig. 2. Graphs of the membership functions of the values of the linguistic variable “Vest”
A fuzzy statement will be called a statement of the form "β IS α", where:
β is a linguistic variable;
α is one of the terms of this variable.
Example: "IS bulletproof vest light." Here, “Bulletproof vest” is a linguistic variable, and “easy” is its meaning.
Simply put, the rule of fuzzy products (hereinafter simply the rule) will be called the classical rule of the form “IF ... THEN ...”, where fuzzy statements will be used as conditions and conclusions. Such rules are written in the following form:
IF (β 1 IS α 1 ) AND (β 2 IS α 2 ) THEN (β 3 IS α 3 ).
In addition to “AND”, the logical link “OR” is also used. But such a record is usually avoided by dividing such rules into somewhat simpler ones (without the “OR”). Also, each of the fuzzy statements in the condition of any rule will be called a sub-condition . Similarly, each of the statements in conclusion is called a sub-statement .
Example: The following examples will help fix the definition:
1) IF (Body armor heavy) THEN (Soldier tired);
2) IF (Male sober) AND (High salary) THEN (wife satisfied).
Everything. This minimum is sufficient for understanding the principles of the algorithm.
Mamdani Algorithm
This algorithm describes several successive stages (Fig. 3). In this case, each subsequent stage receives as input the values obtained in the previous step.

Fig. 3. Diagram of Fuzzy Output Process Activity
The algorithm is notable for the fact that it works on the black box principle. The input receives quantitative values, at the output they are the same. At the intermediate stages, the apparatus of fuzzy logic and the theory of fuzzy sets is used. This is the elegance of using fuzzy systems. You can manipulate the usual numerical data, but at the same time use the flexibility that provide a system of fuzzy inference.
To implement the algorithm, an object-oriented approach was used. The source code is written in the Java programming language. The diagram (Fig. 4) shows the most significant connections and relationships between the classes involved in the algorithm.
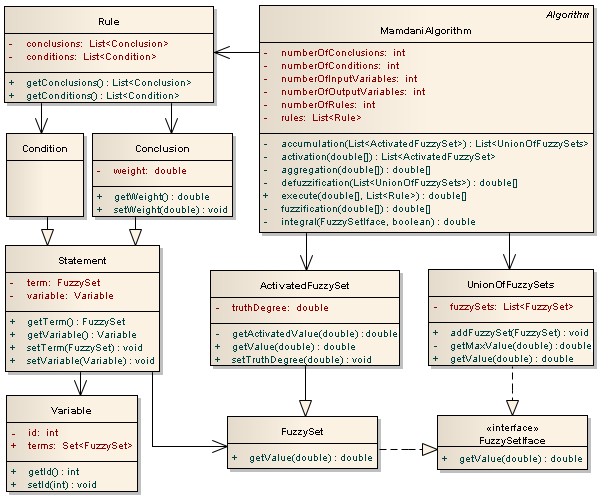
Fig. 4. Class diagram of the implementation of the Mamdani algorithm
Rules (Rule) consist of conditions (Condition) and conclusions (Conclusion), which in turn are fuzzy statements (Statement). A fuzzy statement includes a linguistic variable (Variable) and a term that is represented by a fuzzy set (FuzzySet). The membership function is defined on a fuzzy set, the value of which can be obtained using the getValue () method. This is a method defined in the FuzzySetIface interface. When executing the algorithm, you will need to use the “activated” fuzzy set (ActivatedFuzzySet), which in some way redefines the membership function of the fuzzy set (FuzzySet). The algorithm also uses the union of fuzzy sets (UnionOfFuzzySets). The union is also a fuzzy set, and therefore has an membership function (defined in FuzzySetIface).
The Mamdani algorithm (MamdaniAlgorithm), includes all stages (Fig. 3) and uses the rule base (List <Rule>) as input data. The algorithm also assumes the use of “activated” fuzzy sets (ActivatedFuzzySet) and their associations (UnionOfFuzzySets).
So, the stages of fuzzy output are performed sequentially. And all the values obtained in the previous step can be used in the following.
1. Formation of the rule base
A rule base is a set of rules, where each sub-conclusion is associated with a certain weighting factor.
The rule base can have the following form (for example, the rules of various structures are used):
RULE_1: IF “Condition_1” THEN “Conclusion_1” ( F 1 ) AND “Conclusion_2” ( F 2 );
RULE_2: IF "Condition_2" AND "Condition_3" THEN "Conclusion_3" ( F 3 );
...
RULE_n: IF “Condition_k” THEN “Conclusion_ (q-1)” ( F q-1 ) AND “Conclusion_q” ( F q );
Where F i are weighting factors, meaning the degree of confidence in the truth of the obtained subconclusions ( i = 1 .. q ). By default, the weighting factor is assumed to be 1. The linguistic variables present in the conditions are called input , and in the conclusions output .
Legend:
n is the number of fuzzy product rules (numberOfRules).
m - number of input variables (numberOfInputVariables).
s - number of output variables (numberOfOutputVariables).
k is the total number of sub-conditions in the rule base (numberOfConditions).
q is the total number of sub-conclusions in the rule base (numberOfConclusions).
Note: These symbols will be used in the following steps. In parentheses are the names of the corresponding variables in the source code.
2. Fuzzing input variables
This stage is often referred to as blurring. The generated rule base and the input data array A = {a 1 , ..., a m } are input. This array contains the values of all input variables. The purpose of this stage is to obtain truth values for all sub-conditions from the rule base. This happens as follows: for each of the sub-conditions, the value b i = μ ( a i ) is found. Thus, a set of values b i ( i = 1 .. k ) is obtained.
Implementation:
private double [] fuzzification( double [] inputData) {
int i = 0;
double [] b = new double [numberOfConditions];
for (Rule rule : rules) {
for (Condition condition : rule.getConditions()) {
int j = condition.getVariable().getId();
FuzzySet term = condition.getTerm();
b[i] = term.getValue(inputData[j]);
i++;
}
}
return b;
}Note: The input data array is formed in such a way that the i- th element of the array corresponds to the i- th input variable (the variable number is stored in the integer «id’ field).
3. Aggregation of sub-conditions
As mentioned above, the rule condition can be composite, i.e. include sub-conditions related to each other using the logical AND operation. The purpose of this stage is to determine the degree of truth of the conditions for each rule of the fuzzy inference system. Simply put, for each condition we find the minimum value of the truth of all its sub-conditions. Formally, it looks like this:
c j = min { b i }.
Where:
j = 1 .. n ;
i is a number from the set of numbers of sub-conditions in which the j- th input variable participates.
Implementation:
private double [] aggregation( double [] b) {
int i = 0;
int j = 0;
double [] c = new double [numberOfInputVariables];
for (Rule rule : rules) {
double truthOfConditions = 1.0;
for (Condition condition : rule.getConditions()) {
truthOfConditions = Math .min(truthOfConditions, b[i]);
i++;
}
c[j] = truthOfConditions;
j++;
}
return c;
}4. Activation of sub-conclusions
At this stage there is a transition from the conditions to the sub-conclusions. For each sub-conclusion there is a degree of truth d i = c i * F i , where i = 1 .. q . Then, again, to each i -th subclause, the set D i is associated with a new membership function. Its value is determined at least from d i and the value of the term membership function from the subconclusions. This method is called min-activation, which is formally written as follows:
μ ' i ( x ) = min { d i , μ i ( x )}.
Where:
μ ' i ( x ) - “activated” membership function;
μ i ( x ) - term membership function;
d i - the degree of truth of the i- th sub-conclusion.
So, the goal of this stage is to get a set of “activated” fuzzy sets D i for each of the sub-conclusions in the rule base ( i = 1 .. q ).
Implementation:
private List <ActivatedFuzzySet> activation( double [] c) {
int i = 0;
List <ActivatedFuzzySet> activatedFuzzySets = new ArrayList <ActivatedFuzzySet>();
double [] d = new double [numberOfConclusions];
for (Rule rule : rules) {
for (Conclusion conclusion : rule.getConclusions()) {
d[i] = c[i]*conclusion.getWeight();
ActivatedFuzzySet activatedFuzzySet = (ActivatedFuzzySet) conclusion.getTerm();
activatedFuzzySet.setTruthDegree(d[i]);
activatedFuzzySets.add(activatedFuzzySet);
i++;
}
}
return activatedFuzzySets;
}private double getActivatedValue( double x) {
return Math .min(super.getValue(x), truthDegree);
}5. Accumulation of conclusions
The purpose of this stage is to obtain a fuzzy set (or their union) for each of the output variables. It is executed as follows: the i- th output variable is associated with the union of the sets E i = ∪ D j . Where j is the number of sub-conclusions in which the i -th output variable participates ( i = 1 .. s ). The union of two fuzzy sets is the third fuzzy set with the following membership function:
μ ' i ( x ) = max {μ 1 ( x ), μ 2 ( x )}, where μ 1 ( x ), μ 2 ( x ) are the membership functions of the joined sets.
Implementation:
private List <UnionOfFuzzySets> accumulation( List <ActivatedFuzzySet> activatedFuzzySets) {
List <UnionOfFuzzySets> unionsOfFuzzySets =
new ArrayList <UnionOfFuzzySets>(numberOfOutputVariables);
for (Rule rule : rules) {
for (Conclusion conclusion : rule.getConclusions()) {
int id = conclusion.getVariable().getId();
unionsOfFuzzySets. get (id).addFuzzySet(activatedFuzzySets. get (id));
}
}
return unionsOfFuzzySets;
}private double getMaxValue( double x) {
double result = 0.0;
for (FuzzySet fuzzySet : fuzzySets) {
result = Math .max(result, fuzzySet.getValue(x));
}
return result;
}6. Defusing output variables
The purpose of defuzzification is to obtain a quantitative value (crisp value) for each of the output linguistic variables. Formally, this happens as follows. The i- th output variable and the related set E i ( i = 1 .. s ) are considered. Then using the method of defuzzification is the total quantitative value of the output variable. In this implementation of the algorithm, the center of gravity method is used, in which the value of the i- th output variable is calculated by the formula:
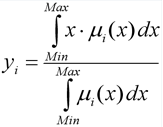
Where:
μ i ( x ) is the membership function of the corresponding fuzzy set E i ;
Min and Max - the boundaries of the universe of fuzzy variables;
y i is the result of defuzzification.
Implementation:
private double [] defuzzification( List <UnionOfFuzzySets> unionsOfFuzzySets) {
double [] y = new double [numberOfOutputVariables];
for ( int i = 0; i < numberOfOutputVariables; i++) {
double i1 = integral(unionsOfFuzzySets. get (i), true );
double i2 = integral(unionsOfFuzzySets. get (i), false );
y[i] = i1 / i2;
}
return y;
}Conclusion
The Mamdani algorithm and many other fuzzy output algorithms are already implemented in such remarkable products as Fuzzy Logic Toolbox (extension for MatLab), fuzzyTECH and many others. Therefore, such a detailed consideration of the algorithm, as in this article, is of more theoretical value than practical. However, I note that only having a solid foundation under you from the knowledge and understanding of the fundamentals of the algorithm, it is possible to apply it with maximum effect.
Literature
For those who want to get acquainted with specific examples of the application of the described algorithm, I recommend turning to the following literature:
1. Leonenkov A.V. Fuzzy modeling in MATLAB and fuzzyTECH / A. Leonenkov. - SPb: BHV-Petersburg, 2003. - 736 p.
2. Shtovba S.D. Design of fuzzy systems using MATLAB / S. Shtovba. - M: Hotline – Telecom, 2007. - 288 p.
Source: https://habr.com/ru/post/113020/
All Articles