Operational Amplifiers (Based on Simplest Examples): Part 3

Brief introduction

I continue to spam writing on the topic of operational amplifiers. In this article I will try to give an overview of one of the most important topics related to the OS. So welcome, active filters .

Topic Overview

You may have come across RC, LC and RLC filters. They are quite suitable for most tasks. But for some purposes it is very important to have filters with more flat characteristics in the passband and steeper slopes. This is where we need active filters.
For a refreshment in memory, let me remind you what filters are:
Low Frequency Filter (LPF) - transmits a signal that is below a certain frequency (it is also called the cutoff frequency). Wikipedia
High Frequency Filter (HPF) - passes the signal above the cutoff frequency. Wikipedia
Bandpass Filter - passes only a certain range of frequencies. Wikipedia
Notch Filter - Delays only a certain range of frequencies. Wikipedia
Well, some more lyrics. Look at the amplitude-frequency response (AFC) of the high-pass filter. On this chart, do not look for anything interesting yet, but just pay attention to the sites and their names:

The most banal examples of active filters can be found here in the section “Integrators and Differentiators”. But in this article we will not touch these schemes, since they are not very effective.

Choose a filter

Suppose you have already decided on the frequency you want to filter. Now you need to decide on the type of filter. More precisely, you need to choose its characteristic. In other words, how the filter will behave.
The main characteristics are:
Filter Buttervorda - has the flattest characteristic in the passband, but has a smooth decline.
Chebyshev filter - has the steepest recession, but it has the most uneven characteristics in the passband.
Bessel filter - has a good phase-frequency response and quite “decent” recession. It is considered the best choice if there is no specific task.

Some more info

Suppose you have done this task. And now you can safely proceed to the calculations.
There are several calculation methods. We will not complicate and use the simplest. And the simplest is the “tabular” method. Tables can be found in the relevant literature. So that you do not search for a long time, I will bring from Horovits and Hill "The Art of Circuit Engineering".
For LPF:

')
Let's just say this is all you could find and read in the literature. We turn specifically to the design of filters.

Payment

In this section I will try to briefly "run through" all types of filters.
So, task # 1 . Build a second-order low-pass filter with a cut-off frequency of 150 Hz according to the Butterworth characteristic.
Let's get started If we have a filter of nth even order, this means that it will have n / 2 opamps. In this task - one.
LPF circuit:

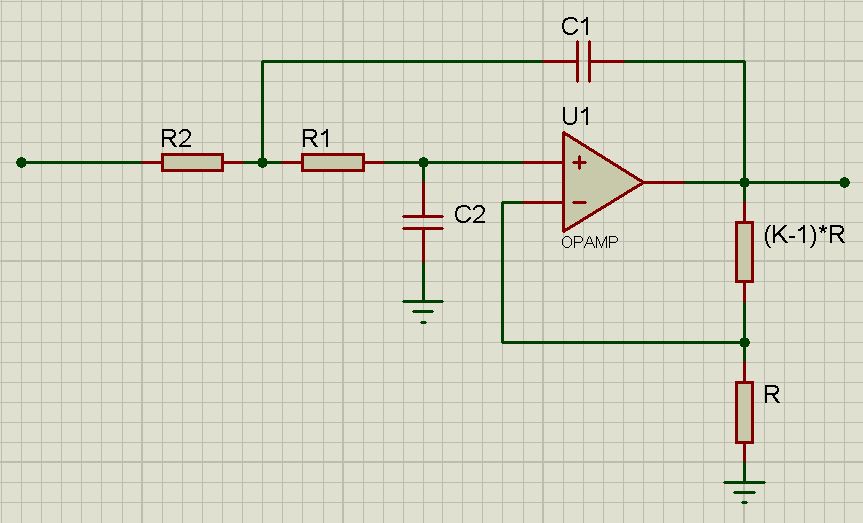
For this type of calculation, it is taken into account that R1 = R2 , C1 = C2 .
We look at the plate. We see that K = 1.586 . This is useful to us later.
For the low pass filter true:
where, of course,
- This is the cutoff frequency.
Making a calculation, we get 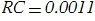. Now let's do the selection of elements. With OS determined - “perfect” in the amount of 1 pc. From the previous equality, we can assume that it does not matter to us which element to choose “first”. Let's start with a resistor. It is best to have its resistance value in the range of 2K ohm to 500 kOhm. In the eye, let it be 11 kΩ. Accordingly, the capacitance of the capacitor will be equal to 0.1 microfarad. For feedback resistors, the value of R is taken arbitrarily. I usually take 10 kΩ. Then, for the upper value of K we take from the table. Therefore, the lower one will have the resistance value R = 10 kΩ, and the upper one 5.8 kΩ.
We collect and model the frequency response.


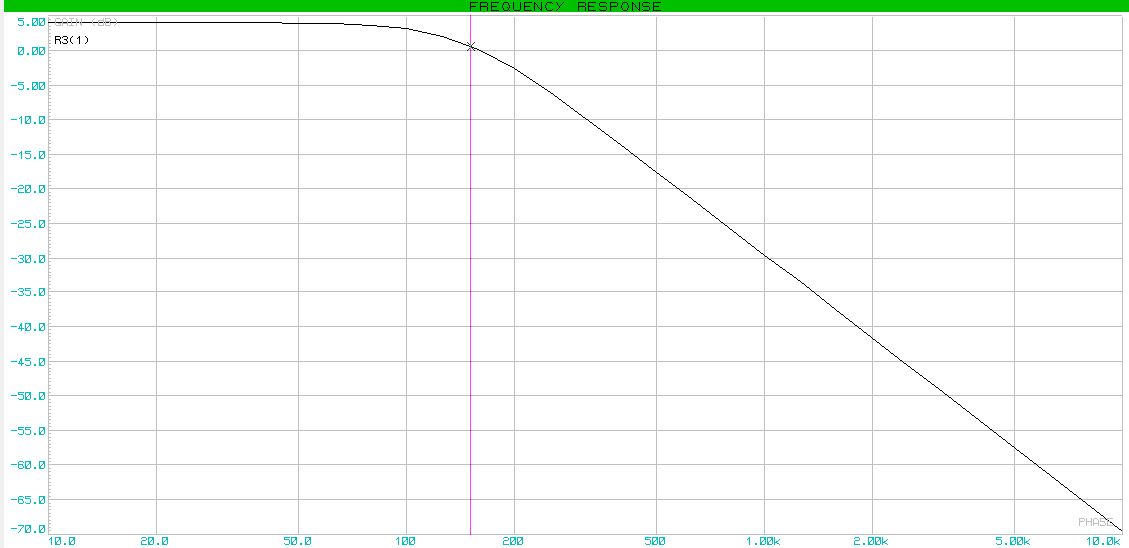
Task # 2 . Build a fourth-order high-pass filter with a cut-off frequency of 800 Hz according to the Bessel characteristic.
We decide. Since the filter is of the fourth order, then there will be two opampies in the scheme. It's all not difficult. We just cascade include 2 high pass filter circuits.
The filter itself looks like this:

The fourth order filter looks like:

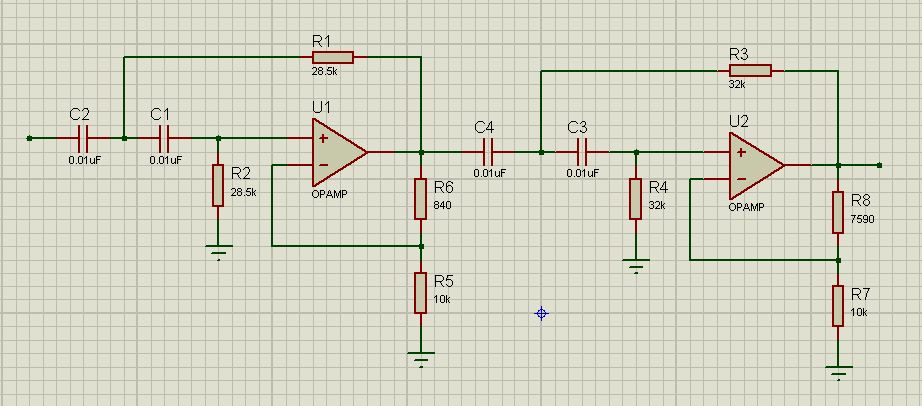
Now the calculation. As you can see, for the fourth order filter, we already have 2 K values. It is logical that the first is intended for the first cascade, the second - for the second. K values ​​are 1.432 and 1.606, respectively. The table was for low pass filters (!). To calculate the highpass filter need to change something. The coefficients K remain the same in any case. For the characteristics of Bessel and Chebyshev, the parameter
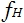- the normalizing frequency. It will be equal now: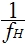

For Chebyshev and Bessel filters, both for low frequencies and high frequencies, the same formula is valid:

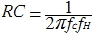
Note that for each individual cascade will have to be considered separately.
For the first cascade:

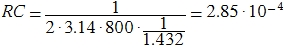
Let C = 0.01 μF, then R = 28.5 kΩ. Feedback Resistors: lower, as usual, 10 kΩ; the top one is 840 ohms.
For the second cascade:

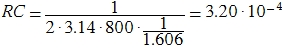
Capacity of the capacitor remains unchanged. Since C = 0.01 μF, then R = 32 kΩ.
Building frequency response.


To create a band-pass or notch-type filters, you can cascade together the low-pass filter and the high-pass filter. But these types are often not used because of poor characteristics.
For bandpass and notch filters you can also use the “tabular method”, but here there are a few other characteristics.
I will give a sign immediately and explain it a little. So as not to stretch too much - the values ​​are taken immediately for a fourth-order band-pass filter.

a1 and b1 are the calculated coefficients. Q - good quality. This is a new parameter. The higher the value of the quality factor, the more dramatic the decline will be. Δf is the range of transmitted frequencies, and the sample is at the level of -3 dB. Coefficient α is another design factor. It can be found using formulas that are fairly easy to find on the Internet.
Okay, that's enough. Now the work assignment.
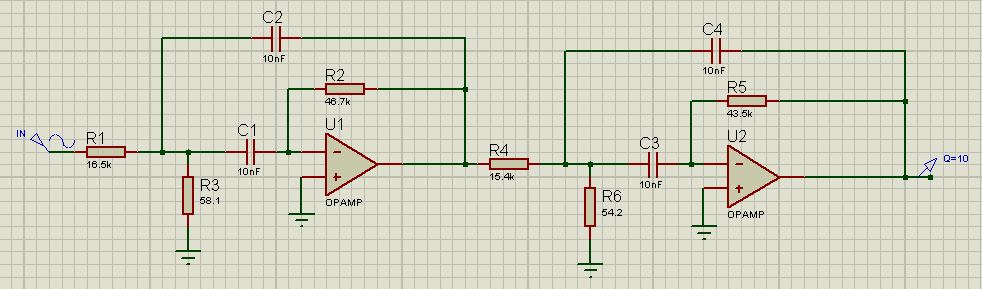
Task # 3 . Build a fourth-order bandpass filter on a Butterworth characteristic with a center frequency of 10 kHz, a width of 1 kHz of transmitted frequencies and a gain at the center frequency point of 1.
Go. Fourth order filter. So two op amps. I will give a typical scheme immediately with design elements.

For the first filter, the center frequency is defined as:

For the second filter:

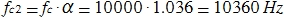
Specifically, in our case, again from the table, we determine that the quality factor is Q = 10. We calculate the quality factor for the filter. Moreover, it is worth noting that the quality factor of both will be equal.

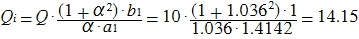
Gain correction for the center frequency region:

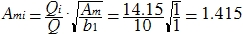
The final stage - the calculation of components.
Let the capacitor be 10 nF. Then, for the first filter:



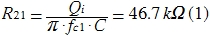
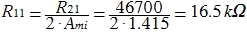
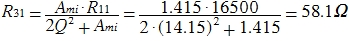
In the same order as (1) we find R22 = R5 = 43.5 kΩ, R12 = R4 = 15.4 kΩ, R32 = R6 = 54.2 Ω. Just keep in mind that for the second filter we use
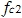
And lastly, the frequency response.


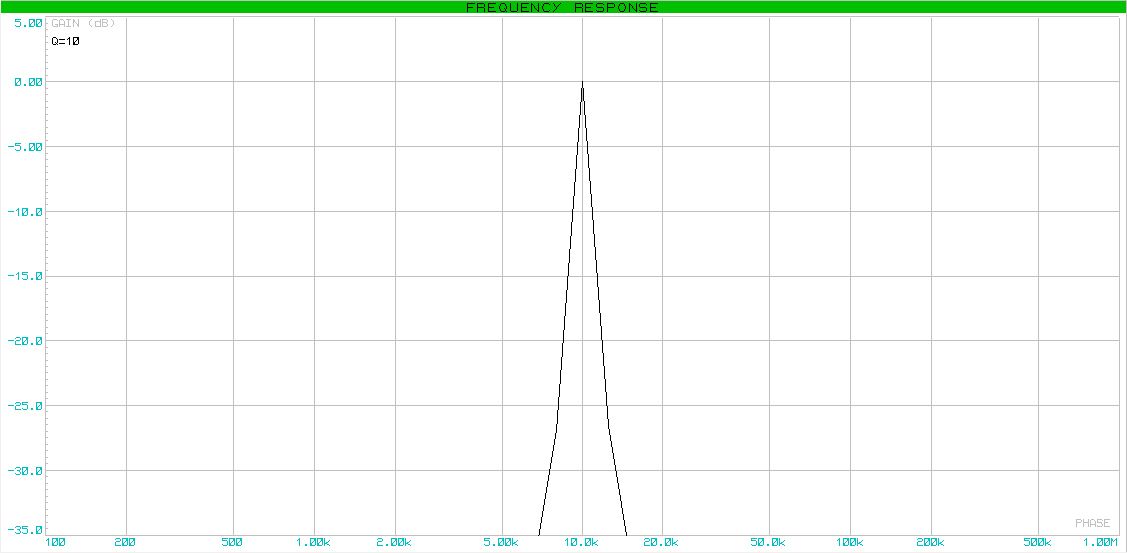
Next stop - bandpass filters or notch filters.
There are several variations. Probably the simplest is the Wien-Robinson Filter (Active Wien-Robinson Filter). A typical circuit is also a 4th order filter.

Our last assignment.
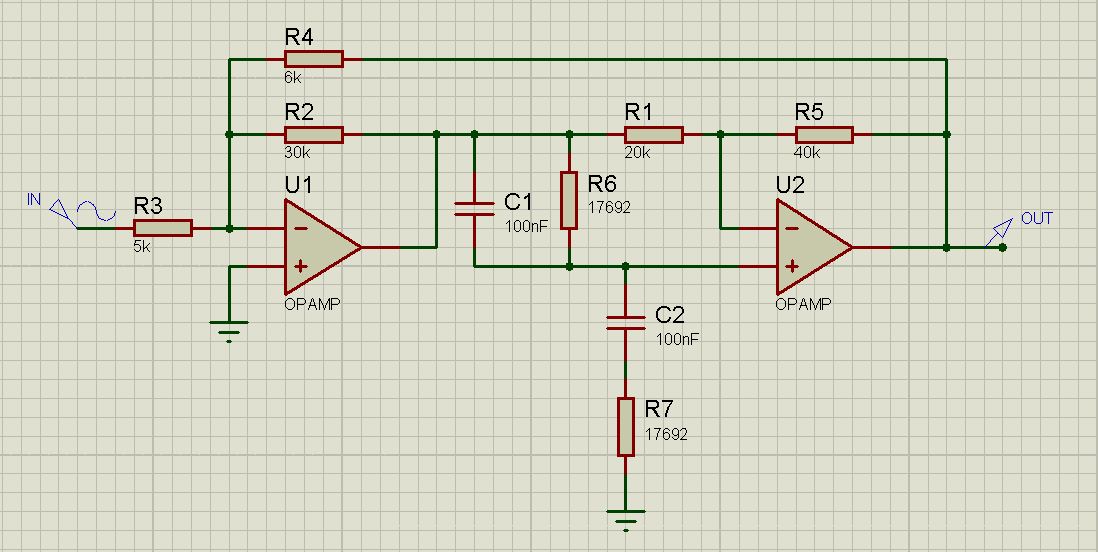
Task # 4 . Build a notch filter with a center frequency of 90 Hz, Q = 2 and a gain in the passband of 1.
First of all, arbitrarily choose the capacitor capacitance. Suppose C = 100 nF.
Determine the value of R6 = R7 = R :

It is logical that "playing" with these resistors, we can change the frequency range of our filter.
Next, we need to determine intermediate factors. We find them through good quality.


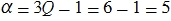
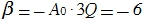
Choose arbitrary resistor R2 . In this particular case, it is best to equal 30 kΩ.
Now we can find resistors that will adjust the gain in the passband.


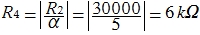
And lastly, you must arbitrarily choose R5 = 2R1 . In my circuit, these resistors have a value of 40 kΩ and 20 kΩ, respectively.
Actually, the frequency response:

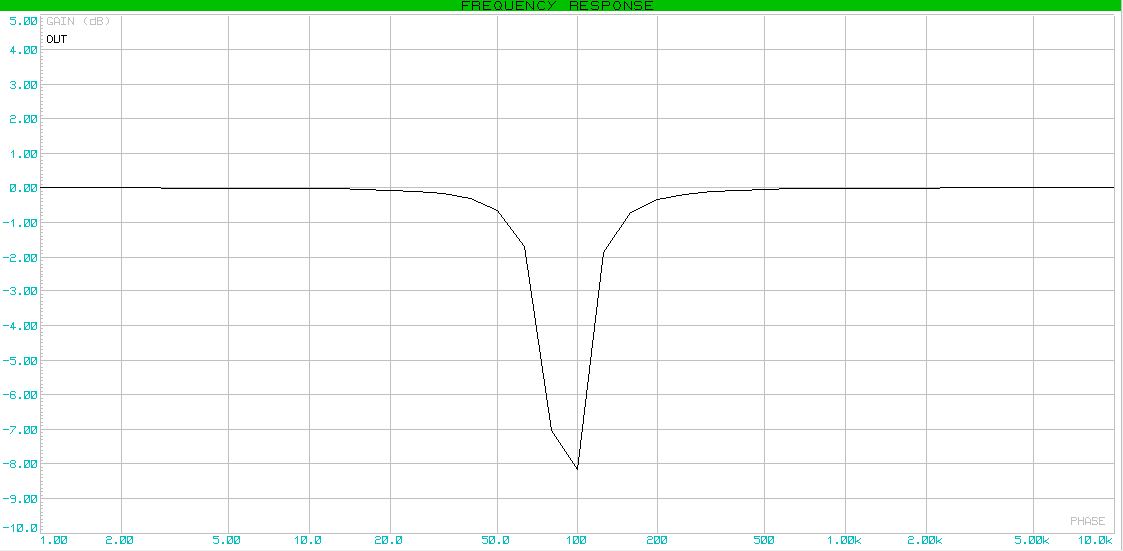
Almost end

Who is interested in learning a little more, I can advise you to read Horowitz and Hill "The Art of Circuit Engineering".
Also, D. Johnson "A handbook of active filters".
Wikipedia
Also, who doesn’t really need calculations, but the filters themselves are needed, I can advise useful software
PS Add a very useful link and its mirror . Thanks for the spiritus_sancti link