A / D conversion for beginners

Introduction

The topics of analog-digital and digital-analog transformations are quite important in the electronics course, since most of the devices that interact with a computer have analog input / output, and the computer can only process digital signals. In this article I want to share with you the very basics of such transformations.

Types of signals

Before you understand the transformations themselves, you need to know what signals exist. And their 3 types:

• Analog
• Discrete
• Digital

Analog signals are continuous in time, they are determined at all points in time.
Discrete are signals represented by a sequence of readings, i.e. signal values ​​at discrete points in time.
Digital signals are discrete in time (or in space) and quantized by level. Computational procedures in a computer are performed precisely in digital signals.

In order for the computer to be able to process the signal, it is necessary to convert the signal from analog to digital form.
After processing, the inverse transform is performed, since most household appliances are controlled by analog signals.

The block diagram of digital signal processing in general is as follows:

')

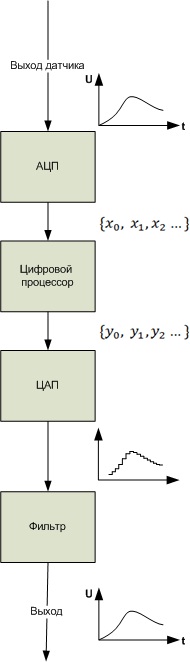
A / D conversion

A / D conversion includes two steps:

1. Signal discretization (in time or space)
2. Level quantization

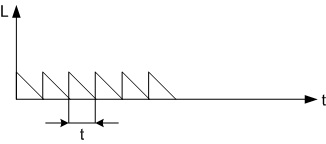
At the stage of sampling, signal samples with a certain sampling period (T) are taken.
The sampling rate can be determined by the formula

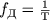
The process of obtaining the sample of the input signal should take a very small part of the sampling period, in order to reduce the dynamic conversion errors caused by the signal change during the sampling time.

The sampling rate is chosen from the Kotelnikov theorem . It argues that in order for the signal samples to be able to restore the continuous signal as accurately as desired, it is necessary that the sampling rate be at least twice as high as the upper frequency of the sample signal.

Any signal has its own spectral representation. Any representation of a signal is a representation in the form of a sum (or integral) of harmonic components (sine waves and cosine waves) of various frequencies taken with specific weights (having a certain amplitude)
For periodic signals, this is the sum; for non-periodic, this is the integral.
The transition to the signal spectrum is carried out using the direct Fourier transform.

Consider the transition to the spectral representation in the form of a periodic function:





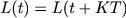
As is well known, a periodic function satisfying the Dirichlet condition can be represented by a series of harmonic functions.



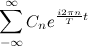
According to the Euler formula, any expression can be represented as
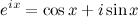
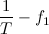- frequency of the first harmonic

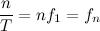- frequency of the n-th harmonic

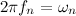- circular frequency of the nth harmonic

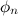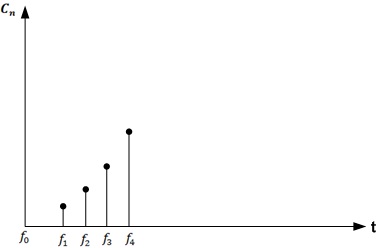
- complex harmonic amplitude, where - phase spectrum.

The set of amplitudes of the harmonics of the Fourier series is called the amplitude spectrum, and the set of their phases is called the phase spectrum.



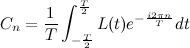
Spectrum example:


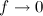For non-periodic function , but then 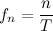is replaced by a continuously varying frequency => the sum is replaced by an integral.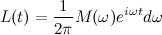

Forward Fourier transform for non-periodic signal

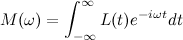
Thus, the spectrum of a non-periodic function is represented by the sum of an infinite number of harmonic oscillations whose frequencies are infinitely close to each other.

Level quantization

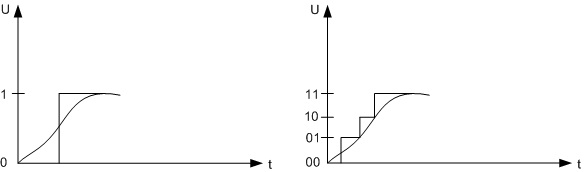
The number of quantization levels is determined by the formula
n is the number of digits
N - quantization level

The choice of the number of quantization levels of signals is made on the basis of a compromise approach, taking into account on the one hand the need for a fairly accurate representation of the signal, which requires a large number of quantization levels, and on the other hand, the number of quantization levels should be less for the code bit to be minimal.

At this point I will finish my article so as not to overload the reader with unnecessary information. Good luck in your endeavors!