Fenwick Tree
Hello, Habrahabr. Now I want to talk about such a data structure as a Fenwick tree. First described by Peter Fenwick in 1994. This structure is similar to the segment tree , but easier to implement.
A Fenwick tree is a data structure, a tree on an array, that has the following properties:
• allows you to calculate the value of some reversible operation F on any segment [L; R] in logarithmic time;
• allows you to change the value of any element for O (log N);
• requires O (N) memory;
Operation F can be selected in different ways, but most often the operations are the sum of the interval, the product of the interval, as well as with a certain modification and restrictions, finding the maximum and finding the minimum on the interval or other operations.
Consider the problem of finding the sum of consecutive elements of an array. Considering the fact that there will be many queries, of the form (L, R), where it is required to find S (L, R) - the sum of all elements from a [L] to a [R] inclusive.
')
The simplest solution to this problem is to find partial sums. After finding them, we write these sums into an array, in which sum [i] = a [1] + a [2] ... + a [i]. Then the required value in the request S (L, R) = sum [R] -sum [L-1] (sum [0] is usually considered to be equal to zero, so as not to consider individual cases).
But this implementation of this task has significant drawbacks. And one of the most important is that when changing one element of the original array, it is necessary to recalculate on average O (N) partial sums, and this is time consuming. You can use the Fenwick tree to solve this problem.
The main advantage of this design is the ease of implementation and speed of responses to requests (for O (1)).
We introduce the function G (x), which is defined in positive integers, and is x & (x + 1) (& is the bitwise AND). Thus, G (x) is x if the last x in the binary decomposition of x is 0 (x is divisible by 2). And if in the binary decomposition of x in the lower digits there is a group of units, then the function is equal to x with the last units replaced by 0. You can verify with examples that this is x & (x + 1) (see the figure).
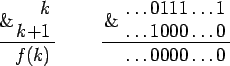
Now we will consider the following partial sums, and write them in t [i] = a [G [i]] + a [G [i] +1] ... + a [i]. Next will be shown how to find these amounts.
To find S (L, R), we search for S (1, L-1) and S (1, R). We write a function that, in the presence of an array t, will find S (L, R). In this case, the left end will not be included in the sum, but it is easy to include it if it is required in the task (see the code).
It is also worth noting that the function G for each application reduces the number of units in the binary record x, by at least 1. From which it follows that the calculation of the amount will be made in O (log N).
Now consider the modification of elements. We need to learn how to quickly change partial amounts depending on how the elements change. We will change a [k] by d. Then we need to change the elements of the array t [j], for which the inequality G (j) <k <j is true. But here comes the following reception. It is argued that all the desired j will belong to the sequence k [i] (see the calculation).

Where under | understand bitwise OR.
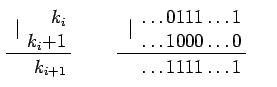
It is easy to see that this function strictly increases, and in the worst case, the logarithm will be applied once, as it adds one unit each time in the binary decomposition of the number k.
We write a function that will change a [k] element by d, and in doing so changes the corresponding partial sums.
Now we note that during the initial calculation of the array t, its initialization with zeros is possible. After that, we apply the upd (i, a [i]) function for each of the N elements. Then, the initial calculation will take O (N * log N) time, which is more than the algorithm described with simple partial sums.
Benefits:
- already mentioned simplicity and speed
- memory takes O (N)
Disadvantages:
- the function must be reversible, which means that the tree cannot count the minimum and maximum (except for the cases when we can donate some data).
We learned how to respond to queries about the sum of elements and modify any element in logarithmic time. This algorithm has many applications, and can help in all tasks where you need to quickly change and determine the result of the operation. I hope everyone was clear and interesting. Thanks for attention.
What is it?
A Fenwick tree is a data structure, a tree on an array, that has the following properties:
• allows you to calculate the value of some reversible operation F on any segment [L; R] in logarithmic time;
• allows you to change the value of any element for O (log N);
• requires O (N) memory;
operation F
Operation F can be selected in different ways, but most often the operations are the sum of the interval, the product of the interval, as well as with a certain modification and restrictions, finding the maximum and finding the minimum on the interval or other operations.
Simplest task
Consider the problem of finding the sum of consecutive elements of an array. Considering the fact that there will be many queries, of the form (L, R), where it is required to find S (L, R) - the sum of all elements from a [L] to a [R] inclusive.
')
The simplest solution to this problem is to find partial sums. After finding them, we write these sums into an array, in which sum [i] = a [1] + a [2] ... + a [i]. Then the required value in the request S (L, R) = sum [R] -sum [L-1] (sum [0] is usually considered to be equal to zero, so as not to consider individual cases).
disadvantages
But this implementation of this task has significant drawbacks. And one of the most important is that when changing one element of the original array, it is necessary to recalculate on average O (N) partial sums, and this is time consuming. You can use the Fenwick tree to solve this problem.
Benefits
The main advantage of this design is the ease of implementation and speed of responses to requests (for O (1)).
Applications of the Fenwick tree for this task
We introduce the function G (x), which is defined in positive integers, and is x & (x + 1) (& is the bitwise AND). Thus, G (x) is x if the last x in the binary decomposition of x is 0 (x is divisible by 2). And if in the binary decomposition of x in the lower digits there is a group of units, then the function is equal to x with the last units replaced by 0. You can verify with examples that this is x & (x + 1) (see the figure).
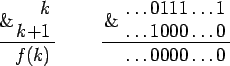
Now we will consider the following partial sums, and write them in t [i] = a [G [i]] + a [G [i] +1] ... + a [i]. Next will be shown how to find these amounts.
Counting the amount
To find S (L, R), we search for S (1, L-1) and S (1, R). We write a function that, in the presence of an array t, will find S (L, R). In this case, the left end will not be included in the sum, but it is easy to include it if it is required in the task (see the code).
const int N=100; int t[N],a[N]; int sum(int L, int R) { int res=0; while (R >= 0) { res += t[R]; R = G( R ) - 1; } while (L >= 0) { res -= t[L]; L = G(L) - 1; } return res; } It is also worth noting that the function G for each application reduces the number of units in the binary record x, by at least 1. From which it follows that the calculation of the amount will be made in O (log N).
Modification of elements
Now consider the modification of elements. We need to learn how to quickly change partial amounts depending on how the elements change. We will change a [k] by d. Then we need to change the elements of the array t [j], for which the inequality G (j) <k <j is true. But here comes the following reception. It is argued that all the desired j will belong to the sequence k [i] (see the calculation).

Where under | understand bitwise OR.
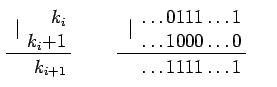
It is easy to see that this function strictly increases, and in the worst case, the logarithm will be applied once, as it adds one unit each time in the binary decomposition of the number k.
We write a function that will change a [k] element by d, and in doing so changes the corresponding partial sums.
const int N=100; int t[N],a[N]; void upd(int k, int d) { a[k]+=d; while(k<N) { t[k]+=d; k=(k|(k+1)); } } Initialization
Now we note that during the initial calculation of the array t, its initialization with zeros is possible. After that, we apply the upd (i, a [i]) function for each of the N elements. Then, the initial calculation will take O (N * log N) time, which is more than the algorithm described with simple partial sums.
Comparison with the segment tree
Benefits:
- already mentioned simplicity and speed
- memory takes O (N)
Disadvantages:
- the function must be reversible, which means that the tree cannot count the minimum and maximum (except for the cases when we can donate some data).
Conclusion
We learned how to respond to queries about the sum of elements and modify any element in logarithmic time. This algorithm has many applications, and can help in all tasks where you need to quickly change and determine the result of the operation. I hope everyone was clear and interesting. Thanks for attention.
Source: https://habr.com/ru/post/112828/
All Articles