Minimization of Boolean Functions by the Hypercube Method
In this article I will talk about a rather important topic in computer science and automata theory - minimization of Boolean functions. Perhaps this question was asked by everyone who studied or encountered this topic.
There are many methods, but those of greatest interest are those that can be formalized and, accordingly, programmed without too much difficulty. As well as working with arbitrary Boolean expressions. The ideal method is not invented, all have certain weak and strong qualities. I will focus on the so-called method of Hypercubes - Quine Method .
The method, unfortunately, is applicable only for Perfect DNFs; therefore, with a large number of variables, the use is complicated by the gigantic expression of the PDNF.
The method is to apply the known rules of bonding and absorption.
')
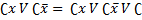

Before describing the algorithm, I will explain why the method is called the hypercube method.
Take an arbitrary function f, M1 (f) - the unit set. Simply put, a set of sets of variables on which the function refers to the correct statement.
A hypercube is a set M1 (f).
A conjunctive monomial implicant if M1 (K) is in M1 (f).
An implicant is called simple if there is no other K2, that M1 (K) is contained in M1 (K2), in simple terms - it corresponds to the largest hypercube.

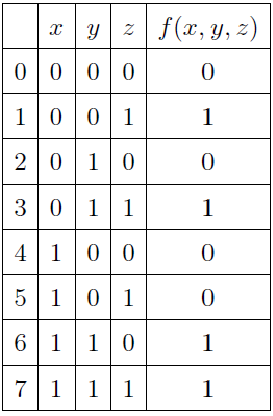
Let's build a truth table for it:
We write out all hypercubes lying in M1 (f) and their corresponding implicants:

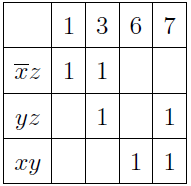
Select simple implicants and build a table of their covers:
Since the implantant yz is overlapped by others, it can be removed from the expression. It turns out that the dead-end DNF function has the form:
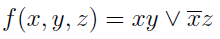
There are many methods, but those of greatest interest are those that can be formalized and, accordingly, programmed without too much difficulty. As well as working with arbitrary Boolean expressions. The ideal method is not invented, all have certain weak and strong qualities. I will focus on the so-called method of Hypercubes - Quine Method .
The method, unfortunately, is applicable only for Perfect DNFs; therefore, with a large number of variables, the use is complicated by the gigantic expression of the PDNF.
The method is to apply the known rules of bonding and absorption.
')
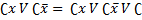

Before describing the algorithm, I will explain why the method is called the hypercube method.
Take an arbitrary function f, M1 (f) - the unit set. Simply put, a set of sets of variables on which the function refers to the correct statement.
A hypercube is a set M1 (f).
A conjunctive monomial implicant if M1 (K) is in M1 (f).
An implicant is called simple if there is no other K2, that M1 (K) is contained in M1 (K2), in simple terms - it corresponds to the largest hypercube.
The main stages of this method
- Build a truth table.
- Write all hypercubes from M1 (f) and implicants.
- Take simple implicants.
- Build a table covering.
- From the remaining simple implicants create a dead-end DNF.
Take the following boolean function as an example.

Let's build a truth table for it:

We write out all hypercubes lying in M1 (f) and their corresponding implicants:

Select simple implicants and build a table of their covers:

Since the implantant yz is overlapped by others, it can be removed from the expression. It turns out that the dead-end DNF function has the form:
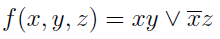
I recommend everyone interested to read the wonderful book by KG Samofalov "Applied Theory of Digital Automatons".
Source: https://habr.com/ru/post/112811/
All Articles