XSD: partial validation
XSD is a language for describing the structure of an XML document. It is also called XML Schema. When using XML Schema, an XML parser can verify not only the correctness of the XML document syntax, but also its structure, content model, and data types. Many one way or another came across a full validation procedure to ensure that the document conforms to a given scheme or to report possible errors. This article will deal with partial validation, in addition to the above, which allows the construction of valid documents on the fly. We will understand what opportunities this approach and ways of its implementation can provide.
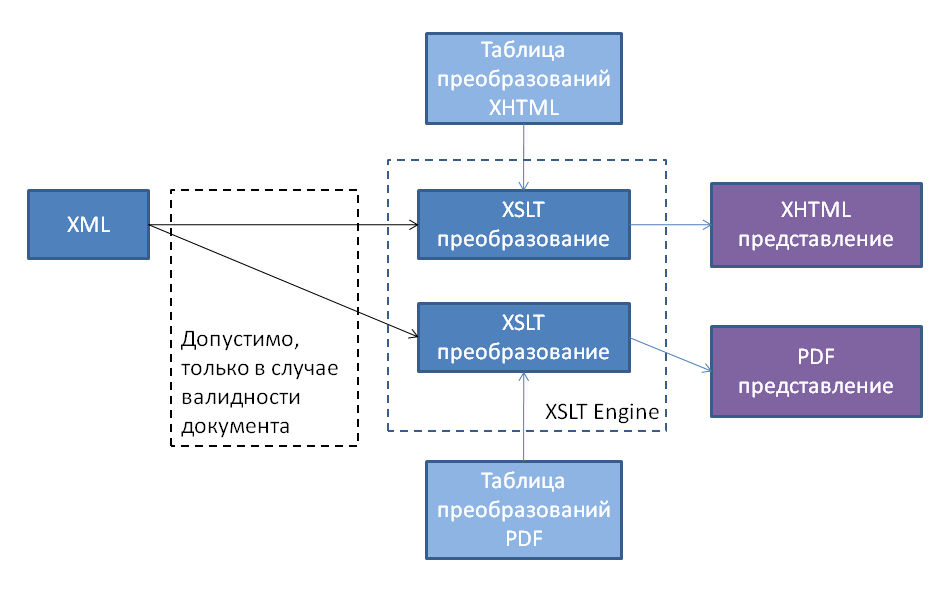
Why in general it may be necessary to construct a document with specified properties, and what properties can we control? The answer to the first question is almost obvious; most documents are not just text, but endowed with some semantics. XML solves the problem of syntactic representation, and the schema partially solves the question of semantic meaning. Due to the document’s compliance with the scheme, it is possible to perform over it a set of predefined actions that are permissible for a whole class of valid documents, be it in a different format, export a significant part of information for a specific task, import new information, taking into account global constraints. The most commonly used mechanism in this case is the XSLT transformation, the meaning of which can be illustrated by the following diagram:
')
The specification of the scheme will completely answer the second question, and we will only dwell on the most important points that give an idea of the capabilities of the schemes. So, the scheme allows:
As a simple example, the article’s table of contents can be given - the schema can be used to specify the semantics of the data “title - page”, check that the pages are ascending, that there are no identical names, that the predefined element “Introduction” goes to the “Literature list” and is required, if there is element "Conclusion". The most complex and powerful example is XML databases , where both the typification and validity of data are determined solely by schemas.
Often there is a desire to modify the document, which already corresponds to the chosen scheme, so that it does not lose validity. Here we are talking about automatic modifications, for example, adding web agents (aggregators) to information in a document or modifying queries in an XML database, as well as manual modification, for example, in a visual XML editor. The operation of full validation for large documents can take significant time, tens of seconds or more, which generally prevents the use of the “atomic change - check - reject / permit” approach. And for visual editors, I would like even more - to be able not only to check the atomic action, but to offer all the options for modifying a specific node that are valid under the scheme. However, good XML editors can do this, and we will try to figure out how they do it.
The W3C XML Schema is an evolution of the XML DTD (Document Type Definition) idea. Both standards describe the document scheme through a set of declarations (parameter objects, elements, and attributes) that describe its class (or type) in terms of the syntactical limitations of this document. The DTD considers a set of regular expressions over atomic terms or elements of a type dictionary. Each type is built on the basis of other types, atomic terms and alternative operations “|”, concatenation “,” and operators “?”, “+”, “*”, Meaning optional, presence of one-or-more or zero-or-more items. XML schema differs from XML DTD syntax, and extends DTD functionality in three ways:
Algorithmically, the validation according to the scheme is a more complicated task than the corresponding task for the DTD [1], but the later standard for describing XML schemas is supplemented by a rule that essentially facilitates validation.
The Unique Particle Attribution (unambiguous definition of particles) rule requires that each element of the document uniquely corresponds to exactly one xsd: element or xsd: any particle in the content model of the parent element [2].
Generally speaking, the Unique Particle Attribution (UPA) rule is not a strict requirement for the structure of XML schemas, but only a highly desirable recommendation and some of the schemes used do not correspond to it. Let us consider the simplest example illustrating the violation of the rule of unambiguous determination of particles.
We define the scheme as follows:
Then an XML document consisting of one element proves a violation of the uniqueness rule; An element can be mapped to both the xsd: elment and xsd: any branches at the same time.
Fortunately, most ready-made schemes follow the UPA rule. Further reasoning will be true only if the scheme complies with the UPA rule, but in general, with minor modifications of the reasoning, it is possible to achieve correctness also on incompatible UPA schemes, due to the loss of speed.
To begin with, we will define elementary changes in the structure, which we will check for correctness:
Now we describe the content model of a complex schema type:
You can go directly to the validation algorithm. The first necessary action is the construction of the correspondence “type of scheme” -> “an automaton that is able to check the descendants of an element of this type for validity”. The task is reduced to two recursive actions:
1. Construction of a non-deterministic finite automaton (NFA) with a given final state S on a given particle:
a. Set the initial state n to S;
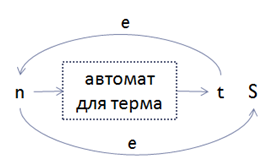
b. If the MaxOccurs particle is infinity (inf):
• Add a new intermediate state t; derived from term conversion to NFA (case 2); add epsilon edges from t to n and from n to s:
c. If the MaxOccurs particles are the number m:
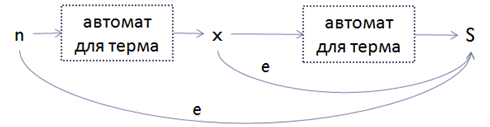
• Build a chain of (MaxOccurs-MinOccurs) term transformations, starting from the final state S, adding epsilon-edge from the intermediate state at each step to the final state S;
For example, for MaxOccurs = 4 and MinOccurs = 2 we get the following automaton:
d. We complete the minOccurs copies of the term transformation from the new initial state n, to the initial state obtained in the previous steps.
2. Construction of a non-deterministic finite automaton with a given receiving state S for a given term:
a. If term is a template (any):
• Create a new state b, and connect it with S edge marked type of term, return b;
b. If term is the item description:
• Create a new state b, then for each element of the permutation group create an edge from b to S, marked with the element type and return b;
c. If term is a choice:
• Create a new state b, create an automaton for each choice (case 1) and connect it with epsilon edges with state b and state S. Return b;
d. If term is a sequence:
• For each selection element, we create an automaton (case 1) and connect the resulting automata in the reverse order, starting with state S, and return the first state in the chain;
Then we apply the Thompson algorithm to the obtained NFA [3], to build deterministic automata. The Thompson algorithm can be applied in the same cases as the algorithm for constructing the deterministic automaton Aho and Ullman, based on folding the equally marked non-epsilon edges [4]. However, in some cases, using the original automaton (created in steps 1–2), the Aho and Ulman algorithm cannot construct a deterministic automaton.
This happens when there are two outgoing edges from the same vertex, such that:
It is easy to show that each case corresponds to the violation of the UPA restriction (the third case has already been considered in the example of a scheme that violates the rule of single-valued determination of particles). Thus, these points do not interfere with the correctness of the solution, and at the output of the algorithm we always get a deterministic finite automaton validating the content of elements of the corresponding type.
We apply the proposed algorithm to each type of circuit and obtain a type -> automaton that can check the descendants of an element of this type.
It remains to solve the last problem - the choice of the desired state machine when validating operations on a given element of the tree. With this, the validation type binding structure (PSVI, Post-Schema-Validation Infoset ), generated by almost any (for example, MSXML or libxml) full validator, will help us. For any element of the tree, it points to the corresponding type in the description of the scheme - exactly the one according to which we generated the necessary automaton.

In our case, the implementation of the PSVI structure is represented by a reference to the type of scheme for each element of the tree.
The MOVE and REMOVE operations do not change the type of the operand (therefore, they do not require changing the PSVI structure), and the ADD operation, together with the addition of the x element, will require adding the x type to the PSVI structure. Thus, together with the change in the structure, we change the information set of the validation type binding, solving the partial validation problem and maintaining the PSVI tree without calling the external validator.
Generally speaking, there will be no direct comparison - after all, we have described an add-in that solves a particular task (ADD / REMOVE / MOVE operations) in a particular case (UPA compliance), but I want to show that in this case it gives a significant speed increase regarding the attempt to use full validation . MSXML6 was chosen as the reference validator generating PSVI, therefore we will compare it with its operation time.
Thus, we obtained a quite admissible average waiting time for checking, which allows implementing the Drag'n'Drop mechanism “on the fly” in the visual editor, and providing a good number of requests per second for a possible XML database.
[1] XML Schema Validator. Thompson, Henry S. and R. Tobin, W3C and University of Edinburgh, 2003.
[2] XML Schema Part 1: Structures. Henry S. Thompson, David Beech, Murray Maloney, Noah Mendelsohn, editors. W3C Recommendation, 2001.
[3] Regular Expression Matching Can Be Simple And Fast. Russ Cox, 2007.
[4] Principles of building compilers. A. Aho. D. Ullman. M .: Mir, 1977.
the main goal
Why in general it may be necessary to construct a document with specified properties, and what properties can we control? The answer to the first question is almost obvious; most documents are not just text, but endowed with some semantics. XML solves the problem of syntactic representation, and the schema partially solves the question of semantic meaning. Due to the document’s compliance with the scheme, it is possible to perform over it a set of predefined actions that are permissible for a whole class of valid documents, be it in a different format, export a significant part of information for a specific task, import new information, taking into account global constraints. The most commonly used mechanism in this case is the XSLT transformation, the meaning of which can be illustrated by the following diagram:

')
The specification of the scheme will completely answer the second question, and we will only dwell on the most important points that give an idea of the capabilities of the schemes. So, the scheme allows:
- Strictly control the typing of data nodes and attributes;
- Determine the order of the nodes, to monitor the presence of mandatory nodes and attributes;
- Require uniqueness of elements in a given context;
- Create variant nodes that require the presence of some attributes or others, depending on the context;
- Require the execution of a specific predicate on a group of nodes or attributes.
As a simple example, the article’s table of contents can be given - the schema can be used to specify the semantics of the data “title - page”, check that the pages are ascending, that there are no identical names, that the predefined element “Introduction” goes to the “Literature list” and is required, if there is element "Conclusion". The most complex and powerful example is XML databases , where both the typification and validity of data are determined solely by schemas.
Often there is a desire to modify the document, which already corresponds to the chosen scheme, so that it does not lose validity. Here we are talking about automatic modifications, for example, adding web agents (aggregators) to information in a document or modifying queries in an XML database, as well as manual modification, for example, in a visual XML editor. The operation of full validation for large documents can take significant time, tens of seconds or more, which generally prevents the use of the “atomic change - check - reject / permit” approach. And for visual editors, I would like even more - to be able not only to check the atomic action, but to offer all the options for modifying a specific node that are valid under the scheme. However, good XML editors can do this, and we will try to figure out how they do it.
Required XML Schema Information
The W3C XML Schema is an evolution of the XML DTD (Document Type Definition) idea. Both standards describe the document scheme through a set of declarations (parameter objects, elements, and attributes) that describe its class (or type) in terms of the syntactical limitations of this document. The DTD considers a set of regular expressions over atomic terms or elements of a type dictionary. Each type is built on the basis of other types, atomic terms and alternative operations “|”, concatenation “,” and operators “?”, “+”, “*”, Meaning optional, presence of one-or-more or zero-or-more items. XML schema differs from XML DTD syntax, and extends DTD functionality in three ways:
- Templates (any, anyType, anyAttribute), allowing to use any element corresponding to the specified namespace;
- The substitution groups that define a set of types that can be used instead of a specific type declaration;
- The number of repetitions, which determines for each element the minimum and maximum allowable number of its occurrences in the type (generalization of the Kleene operators: "*", "+").
Algorithmically, the validation according to the scheme is a more complicated task than the corresponding task for the DTD [1], but the later standard for describing XML schemas is supplemented by a rule that essentially facilitates validation.
The Unique Particle Attribution (unambiguous definition of particles) rule requires that each element of the document uniquely corresponds to exactly one xsd: element or xsd: any particle in the content model of the parent element [2].
Generally speaking, the Unique Particle Attribution (UPA) rule is not a strict requirement for the structure of XML schemas, but only a highly desirable recommendation and some of the schemes used do not correspond to it. Let us consider the simplest example illustrating the violation of the rule of unambiguous determination of particles.
We define the scheme as follows:
<xsd:element name="root">
<xsd:complexType>
<xsd:choice>
<xsd:element name="e1"/>
<xsd:any namespace="##any"/>
</xsd:choice>
</xsd:complexType>
</xsd:element>
Then an XML document consisting of one element proves a violation of the uniqueness rule; An element can be mapped to both the xsd: elment and xsd: any branches at the same time.
Fortunately, most ready-made schemes follow the UPA rule. Further reasoning will be true only if the scheme complies with the UPA rule, but in general, with minor modifications of the reasoning, it is possible to achieve correctness also on incompatible UPA schemes, due to the loss of speed.
Building a validator
To begin with, we will define elementary changes in the structure, which we will check for correctness:
- ADD: creating a sub-element with type x at position n;
- REMOVE: deletes the subitem at position n;
- MOVE: moving an element from position n to position m (although the transfer is reduced to performing deletion and addition of elements, but an intermediate state may violate the validity of the document).
Now we describe the content model of a complex schema type:
- Particle:
• MinOccurs - the minimum number of repetitions of a term (if 0, then the term becomes optional);
• MaxOccurs - the maximum number of repetitions of a term (infinity is allowed - inf).
• Term: element description, pattern, sequence or selection; - Item Description (typedef):
• Local name;
• Namespace name (may be omitted, then the element is considered valid in any namespace);
• Substitution group - the set of all elements taken in expressions containing typedef; - Template (any):
• Name of the namespace valid for the substitution element (may be absent); - Sequence (sequence):
• Consecutive listing of permissible particles; - Choice (choice):
• Set of permissible particles.
You can go directly to the validation algorithm. The first necessary action is the construction of the correspondence “type of scheme” -> “an automaton that is able to check the descendants of an element of this type for validity”. The task is reduced to two recursive actions:
1. Construction of a non-deterministic finite automaton (NFA) with a given final state S on a given particle:
a. Set the initial state n to S;
b. If the MaxOccurs particle is infinity (inf):
• Add a new intermediate state t; derived from term conversion to NFA (case 2); add epsilon edges from t to n and from n to s:

c. If the MaxOccurs particles are the number m:
• Build a chain of (MaxOccurs-MinOccurs) term transformations, starting from the final state S, adding epsilon-edge from the intermediate state at each step to the final state S;
For example, for MaxOccurs = 4 and MinOccurs = 2 we get the following automaton:

d. We complete the minOccurs copies of the term transformation from the new initial state n, to the initial state obtained in the previous steps.
2. Construction of a non-deterministic finite automaton with a given receiving state S for a given term:
a. If term is a template (any):
• Create a new state b, and connect it with S edge marked type of term, return b;
b. If term is the item description:
• Create a new state b, then for each element of the permutation group create an edge from b to S, marked with the element type and return b;
c. If term is a choice:
• Create a new state b, create an automaton for each choice (case 1) and connect it with epsilon edges with state b and state S. Return b;
d. If term is a sequence:
• For each selection element, we create an automaton (case 1) and connect the resulting automata in the reverse order, starting with state S, and return the first state in the chain;
Then we apply the Thompson algorithm to the obtained NFA [3], to build deterministic automata. The Thompson algorithm can be applied in the same cases as the algorithm for constructing the deterministic automaton Aho and Ullman, based on folding the equally marked non-epsilon edges [4]. However, in some cases, using the original automaton (created in steps 1–2), the Aho and Ulman algorithm cannot construct a deterministic automaton.
This happens when there are two outgoing edges from the same vertex, such that:
- Their labels are type descriptions with the same local names and namespace names;
- Their labels are template names, with overlapping areas;
- The label of one edge is a template, the other is a type description, both are in the same namespace, and the type description is included in the template area.
It is easy to show that each case corresponds to the violation of the UPA restriction (the third case has already been considered in the example of a scheme that violates the rule of single-valued determination of particles). Thus, these points do not interfere with the correctness of the solution, and at the output of the algorithm we always get a deterministic finite automaton validating the content of elements of the corresponding type.
We apply the proposed algorithm to each type of circuit and obtain a type -> automaton that can check the descendants of an element of this type.
It remains to solve the last problem - the choice of the desired state machine when validating operations on a given element of the tree. With this, the validation type binding structure (PSVI, Post-Schema-Validation Infoset ), generated by almost any (for example, MSXML or libxml) full validator, will help us. For any element of the tree, it points to the corresponding type in the description of the scheme - exactly the one according to which we generated the necessary automaton.

In our case, the implementation of the PSVI structure is represented by a reference to the type of scheme for each element of the tree.
The MOVE and REMOVE operations do not change the type of the operand (therefore, they do not require changing the PSVI structure), and the ADD operation, together with the addition of the x element, will require adding the x type to the PSVI structure. Thus, together with the change in the structure, we change the information set of the validation type binding, solving the partial validation problem and maintaining the PSVI tree without calling the external validator.
Comparison of results
Generally speaking, there will be no direct comparison - after all, we have described an add-in that solves a particular task (ADD / REMOVE / MOVE operations) in a particular case (UPA compliance), but I want to show that in this case it gives a significant speed increase regarding the attempt to use full validation . MSXML6 was chosen as the reference validator generating PSVI, therefore we will compare it with its operation time.
| The number of elements of the structure | Nesting levels | Number of schema types | Average validation time of MSXML6 | Average validation time using the described add-in |
| 32 | four | sixteen | 10 ms | <1 ms |
| 32 | four | 40 | 16 ms | <1 ms |
| 120,000 | four | sixteen | 51 ms | <2 ms |
| 120,000 | four | 40 | 62 ms | <2 ms |
| 120,000 | 32 | sixteen | 2300 ms | <5 ms |
| 120,000 | 32 | 40 | 2600 ms | <6 ms |
Thus, we obtained a quite admissible average waiting time for checking, which allows implementing the Drag'n'Drop mechanism “on the fly” in the visual editor, and providing a good number of requests per second for a possible XML database.
Links
[1] XML Schema Validator. Thompson, Henry S. and R. Tobin, W3C and University of Edinburgh, 2003.
[2] XML Schema Part 1: Structures. Henry S. Thompson, David Beech, Murray Maloney, Noah Mendelsohn, editors. W3C Recommendation, 2001.
[3] Regular Expression Matching Can Be Simple And Fast. Russ Cox, 2007.
[4] Principles of building compilers. A. Aho. D. Ullman. M .: Mir, 1977.
Source: https://habr.com/ru/post/112500/
All Articles