Monoids and their applications: monoidal calculations in trees
Greetings, Habrahabr. Today I want, in my usual style, to arrange for the community a small educational program on data structures. Only this time it will be much more comprehensive, and its applications and practicality will reach far into the most diverse areas of programming. The most beautiful applications, I, of course, will show and describe directly in the article.
We need a bit of abstract thinking, knowledge of some balanced search tree (for example, the Cartesian tree I described earlier), the ability to read simple C # code, and the desire to apply the knowledge gained.
So, on the agenda today - monoids and their main use for caching calculations in trees.
')
Imagine a set of anything , a set consisting of objects that we are going to manipulate. Call it M. On this set, we introduce a binary operation, that is, a function that associates a new element with a pair of set elements. Hereinafter, we will denote this abstract operation by "⊗", and write the expressions in infix form: if a and b are elements of a set, then c = a ⊗ b is also some element of this set.
For example, consider all the lines that exist in the world. And consider the operation of string concatenation, traditionally denoted in mathematics "◦", and in most programming languages "+":
Or another example is the fst function, known in functional languages when manipulating tuples. Of its two arguments, it returns the first in order as a result. So,fst (5, 2) = 5 ; fst ( . It makes no difference on which set to consider this binary operation, so in your will to choose any.
Next, we impose a restriction of associativity on our operation "⊗". This means that it requires the following: if a sequence of objects is combined with the help of "⊗", then the result should remain the same regardless of the order of application of "⊗". More strictly, for any three objects a , b and c should occur:
( a ⊗ b ) ⊗ c = a ⊗ ( b ⊗ c )
It is easy to see that string concatenation is associative: it does not matter which stitching in the sequence of strings to perform earlier, and which later, in the end, you still get the general merging of all strings in the sequence. The same applies to the fst function, because:
fst ( fst ( a , b ), c ) = a
fst ( a , fst ( b , c )) = a
A chain of applications of fst to a sequence in any order will still produce its head element.
And the last thing we need: in the set M in relation to the operation there must be a neutral element , or a unit of operation. This is an object that can be combined with any element of the set, and it does not change the latter. Formally speaking, if e is a neutral element, then for any a from the set it takes place:
a ⊗ e = e ⊗ a = a
In the example with strings, the neutral element is the empty stringfst ( e , a ) = e is always, and if a ≠ e , then we lose the neutrality property. You can, of course, consider fst on a set of one element, but who needs this boredom? :)
Each such triple <M, ⊗, e> we will solemnly call a monoid . Fix this knowledge in the code:
More examples of monoids, as well as where we actually apply them, will be under the cut.
Before moving on, we must convince the reader that there is darkness and darkness in various monoids in the world. We will use some of them further in the text as examples, others may meet in their practice. I will make a simple list, for each monoid, indicating the set in question, a combining operation and a neutral element. You are invited to verify the associativity of all the operations yourself, I simply don’t have enough space here :) In addition, I’m a little clever and will not include some of the most interesting and unusual monoids in the enumeration, because in the subsequent article they will be devoted to entire chapters.
So, popular monoids:
On it (!) We will finish with examples and we will pass to practice. Before actually presenting this long-awaited practice, I will write down on C # the definitions of a couple of simple monoids from this list, with which we will work in the next chapter.
From this point on we enter the field of practical applications.
First we need a definition of a data structure called Rope . Rare Russian-speaking sources, without further ado, translate it as a rope , I will not back down from this tradition. So, the rope was first proposed in 1995 as a convenient implementation of immutable strings with additional features — for example, a very fast operation of taking substrings and merging strings. With such goals, this structure continues to be used, for example, in the Java library.
Imagine an arbitrary balanced binary tree. Let us suspend the words to this tree as leaves - i.e. character arrays. The resulting tree may look like this:

This data structure will be called a rope .
From past articles on the Cartesian tree, we remember how it is possible in such a tree, for example, to define a character request by index — it is enough to store the sizes of subtrees in intermediate vertices, in this case the total length of the string suspended from the subtree. For this tree, this scheme will look like this:
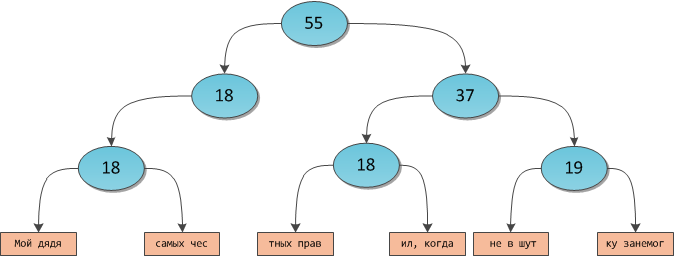
Now, using the familiar algorithm of the K-th ordinal statistics, you can reach the array containing the character under the desired number, and return the desired character by direct indexation in the memory of the array. It is worth noting that on the leaves of the tree arrays are suspended instead of individual characters solely for reasons of optimizing memory on large lines and performance on small ones.
To glue the two ropes, it is enough to create a new root vertex and attach two given trees to it as sons. Since the original trees were balanced, the new rope will also be balanced. Often, people also look at, and if the stitched ropes are not too small, is there no point in combining some sheet segments in the rope-result.
To select a substring in a string, it is enough to apply a simple algorithm, similar to the K-th ordinal statistics. Let it be necessary to select in the rope T a substring of length len , starting with the symbol start .
We first consider two extreme cases.
If
Further, it is possible that the required substring lies entirely in the left subtree, that is,
The symmetric case is the entire substring in the right subtree, that is,
In our example, you can make a call to
 And finally, the most tricky case - the required substring overlaps a piece of both the left and right subtree.
And finally, the most tricky case - the required substring overlaps a piece of both the left and right subtree.
In this case, we will have to select the piece that is included only in the left subtree, then the piece that is included only in the right one, and merge them. We already know how to merge two ropes together.
Determining the indexes of the desired pieces is a snap. Recursive call for the left subtree:
For the right:
Again, we had to pass a zero to the right subtree as a
If these indices do not seem obvious - take a look at the picture.
In the end, recursive calls reach the leaves, in which the query for the substring is already done in the usual linear fashion of the segment. This ensures maximum performance. The overall complexity of the operation is O (log N).
I think there is no need to say that such a data structure can be used not only to implement strings. Any giant sequence of elements can be represented in a similar form, it is enough to choose the optimal length for the underlying leaf segments, and - voila! - we get a convenient data structure for manipulating immutable sequences of colossal length. True, you will say that so far the operations have not been demonstrated enough to serve as a convincing argument for such a transition. Nothing, it's fixable :)
I hope you remember how, using the example of the Cartesian tree, we made multiple requests at sub-slices. In brief, I will remind the essence of the concept: a certain annotation was stored in each vertex of the tree - a parameter equal to the requested value for a subsegment corresponding to the subtree with a root in this vertex. For example, it could be the sum of the elements of a subtree, the maximum of the elements of a subtree, the presence or absence of a Boolean flag on the sub-crop, and so on. When the user wanted to make a request for a subdivision, we didn’t have to re-consider it each time as O (N) for all the sought vertices, because for some subtrees the answers were already cached in the vertices, and it remained only to combine them.
In the Cartesian tree, the Split function did all the “hard work” to restore justice at each vertex for us; we just had to cut the required sub-segment from the tree and take the calculated value as the root of the query response. But you could do otherwise. Remember the algorithm for taking a substring in a rope? He recursively descended from the top to the top, localizing the left and right border of the desired substring, and then merged everything that he finds along the way. This approach could be perfectly applied here.
Consider again the implicit Cartesian tree with annotations — the sums of subtrees — at the vertices, and we will try to make on it a request for the sum in a sub-section
Initialize the result to 0.
At iteration 1, we descend into the left subtree [0; 9]. The result remains 0.
At iteration 2 we descend into the right subtree [5; 9]. The result is increased by the value at the root - 42.
At iteration 3 we descend into the right subtree [8; 9]. The result is increased by the sum of the left subtree [5; 6] plus the value at the root and becomes equal to 42 + 23 + 3 = 68.
At iteration 4, we descend into the left subtree [8; eight]. The result is 68.
At iteration 5, we add to the result the value in the root (29), we get a total of 97, and this is the answer to the problem.
The scheme is very simple, based on the already familiar case analysis at each vertex: how does the requested segment relate to the segments corresponding to my left son, right son and myself? Based on this, we make either one or two recursive calls that calculate the values in the left and right sub-spars and sum them (in the example above, two recursive calls were never needed). Only now in the analysis of cases still have to take into account the data stored in the root.
It is easy to imagine a rope storing segments of numbers in its leaves, and annotations at the vertices corresponding to the amounts in the sub-splines. Then the sum request on any sub-row will be structurally identical to the algorithm for taking a substring from the previous paragraph, only along the way it will accumulate this sum, and returning from recursion add the answer to the result and transfer it higher. , , .
. , , ) ; ) . :
: (C l + C l+1 + … + C r )
: (C l + (((C l+1 + … + C i ) + (C i+1 + … + C j )) + (C j+1 + … + C r-1 ) + … + C r ))
- , , "+" — ! , :) , …
, , , . — , . : , , . , , .
, , . , . .
: , , . , - ! , — . O(log N). Awesome
. . ? Very simple. , . , . : , .
«» — x <, max, -∞>.
« » — x 2 <, +, 0>.
« » — «100% » <, , >. .
, , . Haskell, C# : , !
//. , , , , .
.
, , . . , , « » .
, — , , . . , , — , . , .
p , .
a 1 … a N . - . , .
. :
a 1
a 1 ⊗ a 2
a 1 ⊗ a 2 ⊗ a 3
...
a 1 ⊗ a 2 ⊗ a 3 ⊗… ⊗ a N
"⊗", , — . .
. .
, , False, False True, True .
, False 0, True 1, .
. p ( s ) = { s
— , .

: , — . , «».
, , ,p ( , , , . p ( , , .
, .
, . , . , : « » « ». , .
« » « 256», , , .
. , , split . : , — . split :)
, .
, , , i — « > i ». — , , . — , <, +, 0>. № i — , i .
, , , . «» , . , , . , . , , .
- , . … .
, , . :
N — .
M — .
V — , .
, . , N .


, « ». , :) .
--, , — ? -? - , ? ?
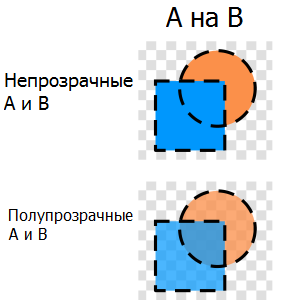
. A B . , X , — . , 1979 Tony Chan, :


, , — . , .
, . , , 0, 0, . , — .
, , pastie.org , :)
, «» K , .. K . , , , . Beauty.
There are two translucent images (with alpha channel). We want to define the overlay operator of two images, better known as alpha composition . Everyone who has ever played with translucent images in Photoshop is familiar with his action.
Images have two parameters for each pixel: color C and alpha channel α . Setting the formulas for calculating these values completely and uniquely defines the overlay operator. So, it turns out that you can easily derive mathematically the following facts:
For proof of these facts and specific formulas I refer you to the corresponding Wikipedia article .
Thus, translucent images on the operation of alpha-composition form a monoid. This gives us the opportunity to process gigantic sets of images that have to be superimposed one after another with the help of the corresponding tree.
, , , , . — , , , . - . -:

.
We need a bit of abstract thinking, knowledge of some balanced search tree (for example, the Cartesian tree I described earlier), the ability to read simple C # code, and the desire to apply the knowledge gained.
So, on the agenda today - monoids and their main use for caching calculations in trees.
')
Monoid as a concept
Imagine a set of anything , a set consisting of objects that we are going to manipulate. Call it M. On this set, we introduce a binary operation, that is, a function that associates a new element with a pair of set elements. Hereinafter, we will denote this abstract operation by "⊗", and write the expressions in infix form: if a and b are elements of a set, then c = a ⊗ b is also some element of this set.
For example, consider all the lines that exist in the world. And consider the operation of string concatenation, traditionally denoted in mathematics "◦", and in most programming languages "+":
"John" ◦ "Doe" = "JohnDoe"Or another example is the fst function, known in functional languages when manipulating tuples. Of its two arguments, it returns the first in order as a result. So,
"foo" , "bar" ) = "foo"Next, we impose a restriction of associativity on our operation "⊗". This means that it requires the following: if a sequence of objects is combined with the help of "⊗", then the result should remain the same regardless of the order of application of "⊗". More strictly, for any three objects a , b and c should occur:
It is easy to see that string concatenation is associative: it does not matter which stitching in the sequence of strings to perform earlier, and which later, in the end, you still get the general merging of all strings in the sequence. The same applies to the fst function, because:
fst ( fst ( a , b ), c ) = a
fst ( a , fst ( b , c )) = a
A chain of applications of fst to a sequence in any order will still produce its head element.
And the last thing we need: in the set M in relation to the operation there must be a neutral element , or a unit of operation. This is an object that can be combined with any element of the set, and it does not change the latter. Formally speaking, if e is a neutral element, then for any a from the set it takes place:
a ⊗ e = e ⊗ a = a
In the example with strings, the neutral element is the empty string
"" : from which side to which line you should not glue it, the string will not change. But the fst in this regard, we are satisfied with the trick: it is impossible to come up with a neutral element for it. Indeed, Each such triple <M, ⊗, e> we will solemnly call a monoid . Fix this knowledge in the code:
public interface IMonoid<T> { T Zero { get; } T Append(T a, T b); } More examples of monoids, as well as where we actually apply them, will be under the cut.
Examples
Before moving on, we must convince the reader that there is darkness and darkness in various monoids in the world. We will use some of them further in the text as examples, others may meet in their practice. I will make a simple list, for each monoid, indicating the set in question, a combining operation and a neutral element. You are invited to verify the associativity of all the operations yourself, I simply don’t have enough space here :) In addition, I’m a little clever and will not include some of the most interesting and unusual monoids in the enumeration, because in the subsequent article they will be devoted to entire chapters.
So, popular monoids:
- <Numbers, +, 0>. By numbers is meant any numerical set - from natural to complex.
- <Numbers, *, 1>.
- <Boolean, &&, True>.
- <Boolean, ||, False>.
- <Strings, concatenation ◦, empty string
"">. - <Lists, concatenation ++, empty list []>.
- <Sets, union ∪, empty set ∅>.
- <Sorted lists, merge, empty list []>. Here merge is understood as the linear operation of merging two ordered lists, surely known to you by the Merge Sort sorting algorithm. By the way, the correctness of the Merge Sort algorithm itself follows precisely from the fact that merge is a monoidal operation. Moreover, an idea similar to its main idea, we will use more than once today.
- <Integers, LCM, 1>.
- <Polynomials of one variable, LCM, 1>.
- <Integers and Polynomials, GCD, 0>. The associativity of the greatest common divisor is clear. As for zero as a neutral element, this property is often assumed by definition, because it is easily consistent with the Euclidean algorithm.
- <Matrices, *, unit matrix>. What is interesting, if we restrict the set to nondegenerate matrices (for which the determinant is not equal to 0), the resulting structure will still remain a monoid - the product of nondegenerate matrices gives a nondegenerate matrix. This simple statement follows from the properties of the determinant.
- <Numbers, min, + ∞>.
- <Numbers, max, -∞>.
- <Permutations of numbers from 1 to N, the product of permutations ◦, the identity permutation (123..N)>.
The product of permutations s and t in discrete mathematics is understood as the following operation: take the number in the first position s , take the number in t by this index and put it in the first position of the result; then we repeat this double indexing for the second position and so on until the Nth. That is, if u = s ◦ t , thenu[i] = t[s[i]], i = 1..N. Permutations and their works are very often found in various problems arising in programming. - Consider some set X. Under X X in mathematics it is customary to denote the set of endomorphisms — arbitrary functions from the set X into it. So, if X is an integer, then any function of the form
int → intis an endomorphism on it. What is the composition of the functions "◦", it is the same "." in Haskell and ">>" in F #, everyone knows.
So, <Endomorphisms, the composition of functions, the identical function id > is a monoid. - Take the usual linear integer operation ("+" or "*") and limit its use to numbers that take the remainder of a certain number P. For example, one can consider multiplication modulo 7, where 3 * 4 = 5, because 12% 7 = 5. The resulting operations on such a set will remain closed and also form a monoid - an extremely important monoid for number theory and cryptography.
By the way, if we take P = 2, then we get bitwise operations. Thus, "&" is multiplication modulo 2, and "^", also known as XOR, is addition modulo 2. Thus,<Boolean, ^, False> is also a monoid. - <Dictionaries (associative arrays), union, empty dictionary>. The data stored in the dictionary itself must form a monoid, thus resolving conflicts when merging:
(map1 ∪ map2)[key] = map1[key] ⊗ map2[key].
Or you can consider not just dictionaries from keys to values (K -> V), but multi-dictionaries from keys to lists of values (K -> [V]), then when combining dictionaries, lists with the same keys can simply be merged using that the lists themselves form a monoid.
On it (!) We will finish with examples and we will pass to practice. Before actually presenting this long-awaited practice, I will write down on C # the definitions of a couple of simple monoids from this list, with which we will work in the next chapter.
All monoids we will implement as singltons. To make it easier to subsequently access the instance for any unknown monoid type, I rendered its creation into a separate static class.
public static class Singleton<T> where T : new() { private static readonly T _instance = new T(); public static T Instance { get { return _instance; } } } public class AddMonoid : IMonoid<int> { public AddMonoid() {} public int Zero { get { return 0; } } public int Append(int a, int b) { return a + b; } } public class FunctionMonoid<T> : IMonoid<Func<T, T>> { public FunctionMonoid() {} public Func<T, T> Zero { get { return x => x; } } public Func<T, T> Append(Func<T, T> f, Func<T, T> g) { return x => g(f(x)); } } public class GCDMonoid : IMonoid<int> { public GCDMonoid() {} private int gcd(int a, int b) { return b == 0 ? a : gcd(b, a % b); } public int Zero { get { return 0; } } public int Append(int a, int b) { return gcd(a, b); } } Where in computer science rope
From this point on we enter the field of practical applications.
First we need a definition of a data structure called Rope . Rare Russian-speaking sources, without further ado, translate it as a rope , I will not back down from this tradition. So, the rope was first proposed in 1995 as a convenient implementation of immutable strings with additional features — for example, a very fast operation of taking substrings and merging strings. With such goals, this structure continues to be used, for example, in the Java library.
Imagine an arbitrary balanced binary tree. Let us suspend the words to this tree as leaves - i.e. character arrays. The resulting tree may look like this:

This data structure will be called a rope .
Access by index
From past articles on the Cartesian tree, we remember how it is possible in such a tree, for example, to define a character request by index — it is enough to store the sizes of subtrees in intermediate vertices, in this case the total length of the string suspended from the subtree. For this tree, this scheme will look like this:

Now, using the familiar algorithm of the K-th ordinal statistics, you can reach the array containing the character under the desired number, and return the desired character by direct indexation in the memory of the array. It is worth noting that on the leaves of the tree arrays are suspended instead of individual characters solely for reasons of optimizing memory on large lines and performance on small ones.
Glueing
To glue the two ropes, it is enough to create a new root vertex and attach two given trees to it as sons. Since the original trees were balanced, the new rope will also be balanced. Often, people also look at, and if the stitched ropes are not too small, is there no point in combining some sheet segments in the rope-result.
Query substring
To select a substring in a string, it is enough to apply a simple algorithm, similar to the K-th ordinal statistics. Let it be necessary to select in the rope T a substring of length len , starting with the symbol start .
We first consider two extreme cases.
If
start = 0len = T.Left.SizeT.Left . Similarly, if start = T.Left.Sizelen = T.Right.SizeT.Right . In the figure above, the second case is implemented if you call the Substring( start : 18, len : 37) function Substring( start : 18, len : 37) , then the function will immediately return the right subtree with the required substring of " , " . " , "Further, it is possible that the required substring lies entirely in the left subtree, that is,
start < T.Left.Sizestart + len ≤ T.Left.SizeThe symmetric case is the entire substring in the right subtree, that is,
start ≥ T.Left.Sizestart + len ≤ T.Left.Size + T.Right.Sizestart size of the left subtree - after all, indexing in the right subtree will start from scratch, it considers itself an independent tree.In our example, you can make a call to
Substring( start : 18, len : 18) . Then, in the first step, the function will determine that it is necessary to descend recursively to the right and make a call to Substring( start : 0, len : 18) on the right subtree. And he, in turn, according to the first case, will return to us entirely his left subtree, corresponding to the substring " , " . " , " And finally, the most tricky case - the required substring overlaps a piece of both the left and right subtree.
And finally, the most tricky case - the required substring overlaps a piece of both the left and right subtree.In this case, we will have to select the piece that is included only in the left subtree, then the piece that is included only in the right one, and merge them. We already know how to merge two ropes together.
Determining the indexes of the desired pieces is a snap. Recursive call for the left subtree:
Substring( start : start, len : T.Left.Size - start)For the right:
Substring( start : 0, len : len - (T.Left.Size - start))Again, we had to pass a zero to the right subtree as a
start argument, because the function on it will work independently.If these indices do not seem obvious - take a look at the picture.
In the end, recursive calls reach the leaves, in which the query for the substring is already done in the usual linear fashion of the segment. This ensures maximum performance. The overall complexity of the operation is O (log N).
Other
I think there is no need to say that such a data structure can be used not only to implement strings. Any giant sequence of elements can be represented in a similar form, it is enough to choose the optimal length for the underlying leaf segments, and - voila! - we get a convenient data structure for manipulating immutable sequences of colossal length. True, you will say that so far the operations have not been demonstrated enough to serve as a convincing argument for such a transition. Nothing, it's fixable :)
As for the choice of structure. You can choose an arbitrary self-balancing binary tree that stores its data in the leaves, for example, a 2-3 tree or a B-tree . Many search trees, created primarily to implement sets, store their data at each vertex, including a red-ebony and a Cartesian tree. Implementing string strings on them is impractical, it will lead to a large number of memory allocations during operations and somewhat complicated code, but the main task of this article is to parameterize trees with monoids - it is easy for both trees of the first and second types. So in the course of the story, I will sometimes refer to the text of an article on the Cartesian tree, and sometimes to the Finger tree , in order to simplify my presentation and not litter it with details of realizations of various balanced trees, which would be completely superfluous here. I hope the reader will perfectly understand and take any approach.
Parameterization, or how to measure a tree
I hope you remember how, using the example of the Cartesian tree, we made multiple requests at sub-slices. In brief, I will remind the essence of the concept: a certain annotation was stored in each vertex of the tree - a parameter equal to the requested value for a subsegment corresponding to the subtree with a root in this vertex. For example, it could be the sum of the elements of a subtree, the maximum of the elements of a subtree, the presence or absence of a Boolean flag on the sub-crop, and so on. When the user wanted to make a request for a subdivision, we didn’t have to re-consider it each time as O (N) for all the sought vertices, because for some subtrees the answers were already cached in the vertices, and it remained only to combine them.
In the Cartesian tree, the Split function did all the “hard work” to restore justice at each vertex for us; we just had to cut the required sub-segment from the tree and take the calculated value as the root of the query response. But you could do otherwise. Remember the algorithm for taking a substring in a rope? He recursively descended from the top to the top, localizing the left and right border of the desired substring, and then merged everything that he finds along the way. This approach could be perfectly applied here.
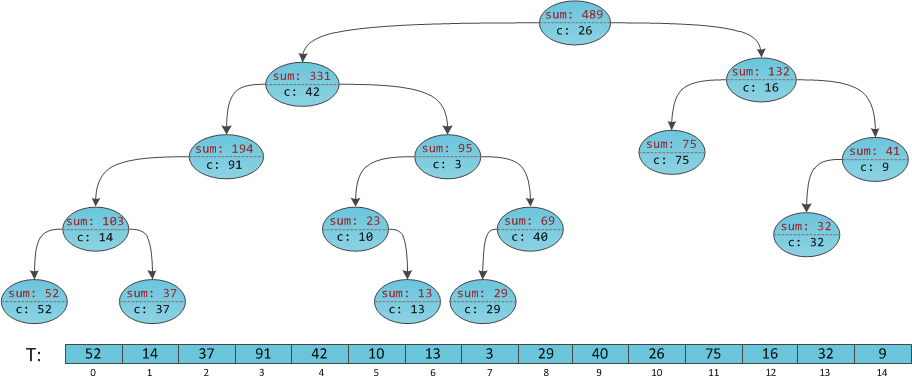
Consider again the implicit Cartesian tree with annotations — the sums of subtrees — at the vertices, and we will try to make on it a request for the sum in a sub-section
[4; 8] [4; 8] .
Initialize the result to 0.
At iteration 1, we descend into the left subtree [0; 9]. The result remains 0.
At iteration 2 we descend into the right subtree [5; 9]. The result is increased by the value at the root - 42.
At iteration 3 we descend into the right subtree [8; 9]. The result is increased by the sum of the left subtree [5; 6] plus the value at the root and becomes equal to 42 + 23 + 3 = 68.
At iteration 4, we descend into the left subtree [8; eight]. The result is 68.
At iteration 5, we add to the result the value in the root (29), we get a total of 97, and this is the answer to the problem.
The scheme is very simple, based on the already familiar case analysis at each vertex: how does the requested segment relate to the segments corresponding to my left son, right son and myself? Based on this, we make either one or two recursive calls that calculate the values in the left and right sub-spars and sum them (in the example above, two recursive calls were never needed). Only now in the analysis of cases still have to take into account the data stored in the root.
It is easy to imagine a rope storing segments of numbers in its leaves, and annotations at the vertices corresponding to the amounts in the sub-splines. Then the sum request on any sub-row will be structurally identical to the algorithm for taking a substring from the previous paragraph, only along the way it will accumulate this sum, and returning from recursion add the answer to the result and transfer it higher. , , .
. , , ) ; ) . :
: (C l + C l+1 + … + C r )
: (C l + (((C l+1 + … + C i ) + (C i+1 + … + C j )) + (C j+1 + … + C r-1 ) + … + C r ))
- , , "+" — ! , :) , …
, , , . — , . : , , . , , .
, , . , . .
: , , . , - ! , — . O(log N). Awesome
. . ? Very simple. , . , . : , .
«» — x <, max, -∞>.
« » — x 2 <, +, 0>.
« » — «100% » <, , >. .
, , . Haskell, C# : , !
//. , , , , .
Tree , , FingerTree . ImplicitTreap , « » , , (null). // , . public interface IMeasured<V> { V Measure { get; } } // : public class IdentityMeasure<T> : IMeasured<T> { public readonly T Data; public IdentityMeasure(T data) { Data = data; } public T Measure { get { return Data; } } } // T - // V - // M - , public class Tree<T, M, V> : IMeasured<V> where M: IMonoid<V>, new() where T: IMeasured<V> { public readonly T Data; // public readonly Tree<T, M, V> Left; public readonly Tree<T, M, V> Right; private readonly V _measure; public V Measure { get { return _measure; } } public Tree(T data) // { Left = Right = null; Data = data; _measure = data.Measure; } public Tree(Tree<T, M, V> left, Tree<T, M, V> right) // { Left = left; Right = right; Data = default(T); _measure = Singleton<M>.Instance.Append(left.Measure, right.Measure); } } // , public class SumTree : Tree<IdentityMeasure<int>, AddMonoid, int> { public SumTree(int data) // : base(new IdentityMeasure<int>(data)) {} public SumTree(SumTree left, SumTree right) // : base(left, right) {} } // , public class PriorityTree : Tree<IdentityMeasure<double>, MaxMonoid, double> { public PriorityTree(double data) // : base(new IdentityMeasure<double>(data)) {} public PriorityTree(PriorityTree left, PriorityTree right) // : base(left, right) {} } .
// . // : Size = 1 + left.Size + right.Size; public readonly int Size = 1; public V MeasureOn(int start, int length) { if (start == 0 && length == Left.Size) return Left.Measure; if (start == Left.Size && length == Right.Size) return Right.Measure; if (start + length <= Left.Size) return Left.MeasureOn(start, length); if (start >= Left.Size) return Right.MeasureOn(start - Left.Size, length); var monoidV = Singleton<M>.Instance; var leftValue = Left.MeasureOn(start, Left.Size - start); var rightValue = Right.MeasureOn(0, length - (Left.Size - start)); return monoidV.Append(leftValue, rightValue); } :
, , . . , , « » .
, — , , . . , , — , . , .
p , .
. :
a 1
a 1 ⊗ a 2
a 1 ⊗ a 2 ⊗ a 3
...
a 1 ⊗ a 2 ⊗ a 3 ⊗… ⊗ a N
"⊗", , — . .
. .
, , False, False True, True .
, False 0, True 1, .
. p ( s ) = { s
"" }.— , .

: , — . , «».
, , ,
" " ) = False" , " ) = True, .
, . , . , : « » « ». , .
« » « 256», , , .
. , , split . : , — . split :)
, .
, . , . .
, , , i — « > i ». — , , . — , <, +, 0>. № i — , i .
, , , . «» , . , , . , . , , .
№1:
- , . … .
, , . :
N — .
M — .
V — , .
, . , N .


, « ». , :) .
--, , — ? -? - , ? ?
. A B . , X , — . , 1979 Tony Chan, :


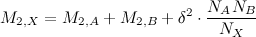
, , — . , .
, . , , 0, 0, . , — .
, , pastie.org , :)
, «» K , .. K . , , , . Beauty.
№2: -

There are two translucent images (with alpha channel). We want to define the overlay operator of two images, better known as alpha composition . Everyone who has ever played with translucent images in Photoshop is familiar with his action.
Images have two parameters for each pixel: color C and alpha channel α . Setting the formulas for calculating these values completely and uniquely defines the overlay operator. So, it turns out that you can easily derive mathematically the following facts:
- The overlap operator is associative;
- Any image with an alpha channel of 0 is used for the overlay operator by one.
For proof of these facts and specific formulas I refer you to the corresponding Wikipedia article .
Thus, translucent images on the operation of alpha-composition form a monoid. This gives us the opportunity to process gigantic sets of images that have to be superimposed one after another with the help of the corresponding tree.
Example # 3: regular expressions
, , , , . — , , , . - . -:

.
Source: https://habr.com/ru/post/112394/
All Articles