Dynamics by sub-cuts: basic things and “one is good and two are better”
Good evening.
In this post I will analyze the problem B "Oaks" from the practical tour of the city Olympiad of St. Petersburg schoolchildren in computer science.
This is a task for dynamic programming in subsegments and the idea of a solution is interesting because it is more convenient to calculate two dynamics instead of one. If you are interested (ignorance of the dynamics does not release, but it will be more difficult) - welcome.
First you can see the condition of the problem. Together with the tests it lies here (only the conditions can be downloaded from min.us).
After recounting the legend, the following task remains:
If you want, you can think (the name of the post can tell you).
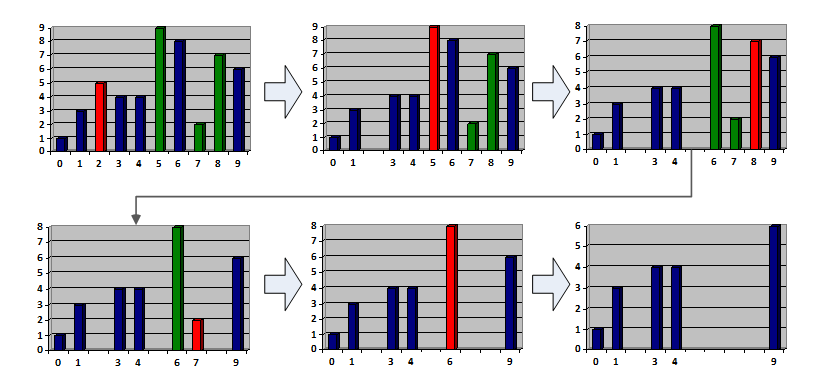
As you can guess from the tags - the solution is a kind of dynamics. If you have forgotten or did not know what dynamic programming is, I will remind you. The idea of the dynamics is that for very small examples (for example, one tree) the answer is obvious (not to cut anything), and for large ones you can get a solution, knowing solutions for some smaller independent subtasks. At this point, the dynamics are very similar to induction. How to reduce the task, for example, for ten trees to smaller? Suppose we already know the answer (we will not use it, but it is useful to present it). It has two extreme trees and some kind of middle. Let's iterate over any tree from this middle (in general, any tree that lies in height between the boundaries - otherwise it cannot be left):
You may notice that all operations will be performed either on the left or on the right. It means that they are independent of each other. Here also broke into two independent subtasks. You can pre-relax (choose the best) answer on our large segment.
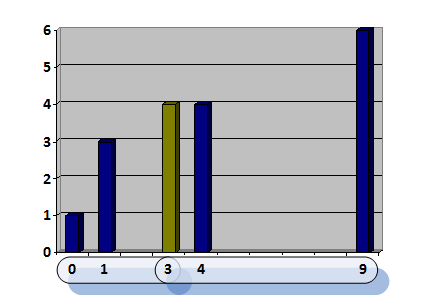
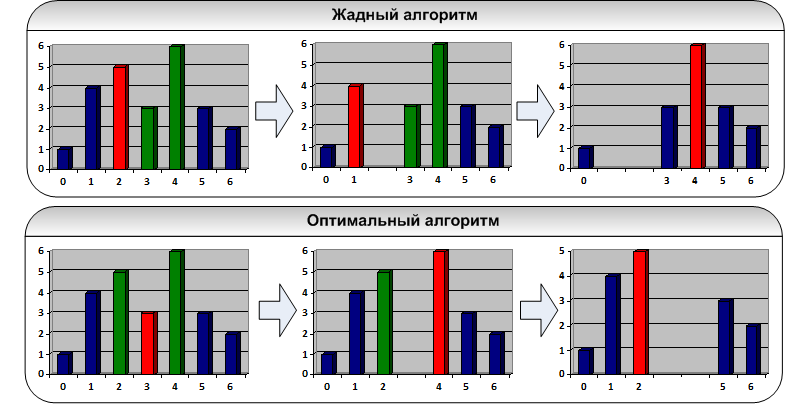
And what to do when there are no trees in the segment between our borders (for example, trees 4 and 9)? Here we understand that in this case we need to cut down all the trees in the interval. The question is - in what order? There is a temptation to make a greedy algorithm: cut down the first tree and so on until they run out. However, it is incorrect:
I think it’s obvious that you shouldn’t think of various optimizations in the style “run the search in the last two steps” and so on - it all breaks off with a big random test.
Need something smarter. We look at the name of the post one more time and come up with a very similar dynamic along the sub-cuts: for two trees and less, nothing at all is necessary to delete. And for more, you need to sort out the tree, which we will delete last and notice that we again received two subtasks: left and right. The only distinguishing point is to check that this tree can be deleted at the end (when the interval borders become its neighbors)
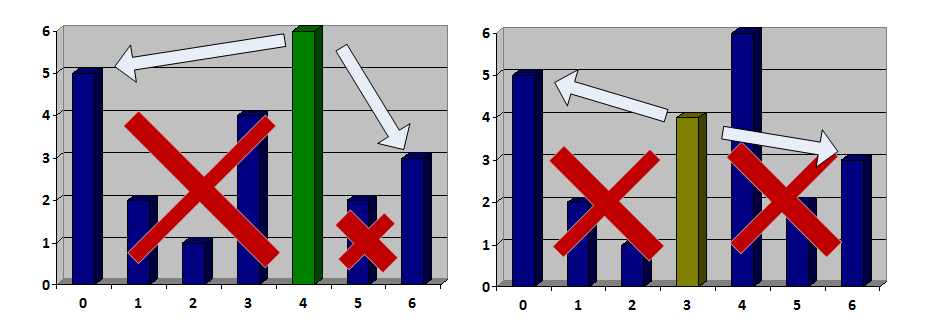
For example, you can delete the last 4 tree, and 3 - you can not.
The answer is restored by the classical method - we remember the optimal transition from each state (where the best answer was achieved) to the array, and then we go from the end. In the dynamics of sub-cuts, recovery is convenient to write recursively:
In total, we have O (n 2 ) states of each dynamics (one for each sub-segment). In each dynamics, the transition is made in O (n) - to iterate the tree inside the interval. When the answer is restored, each state is visited no more than once. It turns out a square, but since it is asympotically (infinitely less on infinitely large n ) less than a cube, then it can be neglected.
The total running time is O (n 3 ) , which for n = 200 is O (8 * 10 6 ) , which works out instantly. It suits us too.
First you need to read the data in an array / vector. You know how to do it.
Next, you need to calculate the dynamics to remove all trees. We will store it in the array int del [a] [b] - -1 if it is impossible to delete all the trees in the interval (a, b) , and the number of the last tree is different.
There is a temptation to search for two sub-cuts to write two cycles:
However, this is fundamentally wrong, since the transition of dynamics will be correct only when we know the answer for the “smaller” subtasks. In our case - for smaller sub-cuts. Therefore, you must first go through the length of the segment, and then - the beginning (or end):
In this cycle, you need to sort out the last tree and check the possibility of deletion. Also, do not forget to initialize the dynamics for empty intervals:
The second dynamic will be stored in two arrays - int dyn [a] [b] and int fr [a] [b] . The first one is, in fact, the answer for a subsegment (how many trees must be removed at least), or infinity (I use 10 9 ), if one cannot leave a non-decreasing subsequence. And in the second array, we will store either -1 , if the first one contains infinity, or the last deleted tree.
So we write. Here you can initialize everything along the way (a separate cycle is needed only to fill with infinity):
It was already fully written above - that code works completely. It remains only to verify that there is an answer, call the function, and output the result:
The entire program can be viewed on pastebin . Since it was written at the Olympiad, it contains some abbreviations for speed dialing and no comments. However, I cited all the significant code in the article.
On the topic of testing algorithmic problems, you can write a lot of great articles. But we want to quickly, right? Therefore, we recall where we downloaded the tests at the beginning of the article, unpack them somewhere (the task is called oaks ) and either run all 50 tests with pens, or compile the file check.dpr ( compiled ) and write the script on CMD:
We start. If you saw ALL IS OK! and "Press Any Key" - your decision is right. If not, then there is a test on which it works incorrectly. Do not rush to watch this test - it will be much more useful to find and fix the bug yourself.
That's all I wanted to tell. I hope you understand everything and I have not wasted your time.
Thank you for your attention, easy accepts.
I will be glad to constructive criticism.
In this post I will analyze the problem B "Oaks" from the practical tour of the city Olympiad of St. Petersburg schoolchildren in computer science.
This is a task for dynamic programming in subsegments and the idea of a solution is interesting because it is more convenient to calculate two dynamics instead of one. If you are interested (ignorance of the dynamics does not release, but it will be more difficult) - welcome.
Condition
First you can see the condition of the problem. Together with the tests it lies here (only the conditions can be downloaded from min.us).
After recounting the legend, the following task remains:
- There are n (2 <= n <= 200) oaks, each one has a height - an integer from 1 to 1000 (on).
- We can: remove an oak from a sequence if:
- Either it is strictly less than both neighbors.
- Or strictly more than their
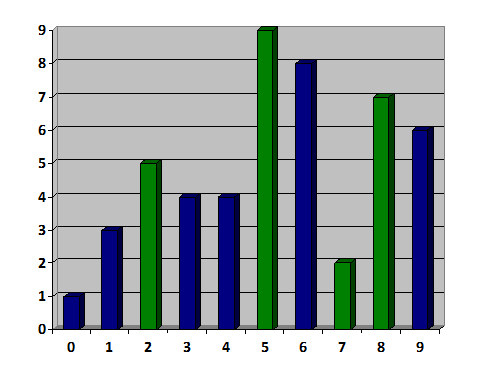
For example, in the following image, green oaks are highlighted, which can be deleted:

- It is necessary for the minimum number of operations to turn the sequence into a slightly increasing. The sequence of deletions must also be displayed. For example:

If you want, you can think (the name of the post can tell you).
main idea
As you can guess from the tags - the solution is a kind of dynamics. If you have forgotten or did not know what dynamic programming is, I will remind you. The idea of the dynamics is that for very small examples (for example, one tree) the answer is obvious (not to cut anything), and for large ones you can get a solution, knowing solutions for some smaller independent subtasks. At this point, the dynamics are very similar to induction. How to reduce the task, for example, for ten trees to smaller? Suppose we already know the answer (we will not use it, but it is useful to present it). It has two extreme trees and some kind of middle. Let's iterate over any tree from this middle (in general, any tree that lies in height between the boundaries - otherwise it cannot be left):

You may notice that all operations will be performed either on the left or on the right. It means that they are independent of each other. Here also broke into two independent subtasks. You can pre-relax (choose the best) answer on our large segment.
And what to do when there are no trees in the segment between our borders (for example, trees 4 and 9)? Here we understand that in this case we need to cut down all the trees in the interval. The question is - in what order? There is a temptation to make a greedy algorithm: cut down the first tree and so on until they run out. However, it is incorrect:

I think it’s obvious that you shouldn’t think of various optimizations in the style “run the search in the last two steps” and so on - it all breaks off with a big random test.
Need something smarter. We look at the name of the post one more time and come up with a very similar dynamic along the sub-cuts: for two trees and less, nothing at all is necessary to delete. And for more, you need to sort out the tree, which we will delete last and notice that we again received two subtasks: left and right. The only distinguishing point is to check that this tree can be deleted at the end (when the interval borders become its neighbors)

For example, you can delete the last 4 tree, and 3 - you can not.
Recovery response
The answer is restored by the classical method - we remember the optimal transition from each state (where the best answer was achieved) to the array, and then we go from the end. In the dynamics of sub-cuts, recovery is convenient to write recursively:
Recovery response
vector < int > ans ; //
// a b - ,
void deleteAll ( int a, int b ) {
assert ( del [ a ] [ b ] >= 0 ) ;
if ( del [ a ] [ b ] == a ) return ;
deleteAll ( a, del [ a ] [ b ] ) ;
deleteAll ( del [ a ] [ b ] , b ) ;
ans. push_back ( del [ a ] [ b ] ) ;
}
//
void restoreAns ( int a, int b ) {
assert ( fr [ a ] [ b ] >= 0 ) ;
if ( fr [ a ] [ b ] == a ) {
deleteAll ( a, b ) ;
return ;
}
restoreAns ( a, fr [ a ] [ b ] ) ;
restoreAns ( fr [ a ] [ b ] , b ) ;
}Working hours
In total, we have O (n 2 ) states of each dynamics (one for each sub-segment). In each dynamics, the transition is made in O (n) - to iterate the tree inside the interval. When the answer is restored, each state is visited no more than once. It turns out a square, but since it is asympotically (infinitely less on infinitely large n ) less than a cube, then it can be neglected.
The total running time is O (n 3 ) , which for n = 200 is O (8 * 10 6 ) , which works out instantly. It suits us too.
How to write
First you need to read the data in an array / vector. You know how to do it.
First dynamic
Next, you need to calculate the dynamics to remove all trees. We will store it in the array int del [a] [b] - -1 if it is impossible to delete all the trees in the interval (a, b) , and the number of the last tree is different.
There is a temptation to search for two sub-cuts to write two cycles:
for ( int left = 0 ; left < n ; left ++ )
for ( int right = left ; right < n ; right ++ ) {
// ...
}However, this is fundamentally wrong, since the transition of dynamics will be correct only when we know the answer for the “smaller” subtasks. In our case - for smaller sub-cuts. Therefore, you must first go through the length of the segment, and then - the beginning (or end):
for ( int l = 2 ; l < n ; l ++ )
for ( int a = 0 ; a + l < n ; a ++ ) {
int b = a + l ;
// ...
}In this cycle, you need to sort out the last tree and check the possibility of deletion. Also, do not forget to initialize the dynamics for empty intervals:
// h2, h1 h3
bool can ( int h1, int h2, int h3 ) {
if ( h1 < h2 && h3 < h2 ) return true ;
if ( h1 > h2 && h3 > h2 ) return true ;
return false ;
}
// ...
for ( int a = 0 ; a + 1 < n ; a ++ )
del [ a ] [ a + 1 ] = a ;
for ( int l = 2 ; l < n ; l ++ )
for ( int a = 0 ; a + l < n ; a ++ ) {
int b = a + l ;
for ( int i = a + 1 ; i < b ; i ++ )
if ( del [ a ] [ i ] >= 0 && del [ i ] [ b ] >= 0 && can ( h [ a ] , h [ i ] , h [ b ] ) ) {
del [ a ] [ b ] = i ;
break ;
}
}Second dynamic
The second dynamic will be stored in two arrays - int dyn [a] [b] and int fr [a] [b] . The first one is, in fact, the answer for a subsegment (how many trees must be removed at least), or infinity (I use 10 9 ), if one cannot leave a non-decreasing subsequence. And in the second array, we will store either -1 , if the first one contains infinity, or the last deleted tree.
So we write. Here you can initialize everything along the way (a separate cycle is needed only to fill with infinity):
//
for ( int l = 1 ; l < n ; l ++ )
for ( int a = 0 ; a + l < n ; a ++ ) {
int b = a + l ;
if ( h [ a ] > h [ b ] ) continue ; // ,
if ( del [ a ] [ b ] >= 0 ) { // ,
dyn [ a ] [ b ] = b - a - 1 ;
fr [ a ] [ b ] = a ;
}
for ( int i = a + 1 ; i < b ; i ++ ) {
// , ,
// -
if ( h [ a ] > h [ i ] || h [ i ] > h [ b ] ) continue ;
// ,
// ,
int cans = dyn [ a ] [ i ] + dyn [ i ] [ b ] ;
if ( dyn [ a ] [ b ] > cans ) {
dyn [ a ] [ b ] = cans ;
fr [ a ] [ b ] = i ;
}
}
}Recovery response
It was already fully written above - that code works completely. It remains only to verify that there is an answer, call the function, and output the result:
int a = 0 , b = n - 1 ;
if ( fr [ 0 ] [ n - 1 ] < 0 ) printf ( "-1 \n " ) ;
else {
ans = vector < int > ( ) ;
restoreAns ( a, b ) ;
printf ( "%d \n " , ans. size ( ) ) ;
for ( int i = 0 ; i < ans. size ( ) ; i ++ )
printf ( "%d \n " , ans [ i ] + 1 ) ;
}Together
The entire program can be viewed on pastebin . Since it was written at the Olympiad, it contains some abbreviations for speed dialing and no comments. However, I cited all the significant code in the article.
Testing
On the topic of testing algorithmic problems, you can write a lot of great articles. But we want to quickly, right? Therefore, we recall where we downloaded the tests at the beginning of the article, unpack them somewhere (the task is called oaks ) and either run all 50 tests with pens, or compile the file check.dpr ( compiled ) and write the script on CMD:
@echo off
for %% i IN ( tests\ ?? ) DO (
del oaks. in oaks. out > nul 2 >& 1
copy %% i oaks. in > nul 2 >& 1
main > nul 2 >& 1
if errorlevel 1 exit
check oaks. in oaks. out %% i. a
if errorlevel 1 exit
)
echo ALL IS OK !
pauseWe start. If you saw ALL IS OK! and "Press Any Key" - your decision is right. If not, then there is a test on which it works incorrectly. Do not rush to watch this test - it will be much more useful to find and fix the bug yourself.
Conclusion
That's all I wanted to tell. I hope you understand everything and I have not wasted your time.
Thank you for your attention, easy accepts.
I will be glad to constructive criticism.
')
Source: https://habr.com/ru/post/112386/
All Articles