Bloom filter
Hello again! Today I will tell about Bloom's filter - the data structure is ingenious in its simplicity. In essence, this filter implements a probabilistic set with only two operations: adding an element to the set and checking whether the element is in a set. The set is probabilistic because the last operation to the question “does this element belong to the set?” Gives an answer not in the form of “yes / no”, but in the form of “possible / no”.
As I said, the idea to genius is simple. An array of bits of fixed size
To verify the membership, you guessed it, it is enough to count the hash functions for the potential member and make sure that all the corresponding bits are set to one - this will be the answer “possible”. If at least one bit is not equal to one, then the set of this element does not contain - the answer is “no”, the element is filtered.
')
JavaScript code, simply because on Habré it is understandable to many. First of all, we need to somehow represent the bitmap:
Also, we need a parameterized family of hash functions to make it easier to create
Well, actually, the Bloom filter itself:
Example of use:
After the games with the parameters, it becomes clear that there must be some optimal values for them.
Of course, I did not deduce the theoretical optimal values myself, I just went to Wikipedia, but even without it, by turning on the logic, one can estimate and catch some regularities. For example, it makes no sense to use a large bitmap if you are going to store two values there, the opposite is also true, otherwise the array will be overcrowded, which will lead to an increase in erroneous answers “possible”. The optimal array size in bits:
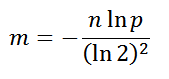
where
The number of hash functions should not be large, but not small. The optimal amount:

Apply the knowledge gained:
For example, Googol uses Bloom filters in its BigTable to reduce disk accesses. It is not surprising, because in fact, BigTable is a large, very sparse multidimensional table, so most of the keys point to emptiness. In addition, the data is sawn into relatively small block files, each of which is queried for requests, although it may not contain the required data.
In this case, it is advantageous to spend some RAM and greatly reduce disk usage. For example, to reduce the load by 10 times, you need to store about 5 bits of information for each key. To reduce 100 times, you need about 10 bits per key. Draw your own conclusions.
Judging by the tests, the optimal values of the parameters for the practice are somewhat overestimated; we can safely lower the false response threshold by an order of two. Just be sure to test it if you use it - maybe some kind of unique combination of data and hash functions came up in my tests, or I just made a mistake somewhere.
Obviously, it is impossible to remove elements from the filter, but this is simply solved - it is enough to replace the bit array with an array of counters - increment when adding, decrement when deleting. Memory consumption naturally increases.
It is also obvious that it is impossible to dynamically change the filter parameters. The problem is elegantly solved by the introduction of a hierarchy of filters, each subsequent more accurate, if necessary, the hierarchy grows deep into.
Perhaps that's all. Until.
How does the filter do this?
As I said, the idea to genius is simple. An array of bits of fixed size
m and a set of k different hash functions are produced, giving values from 0 to m - 1 . If it is necessary to add an element to the set, the value of each hash function is considered for the element and bits with corresponding indices are set in the array.To verify the membership, you guessed it, it is enough to count the hash functions for the potential member and make sure that all the corresponding bits are set to one - this will be the answer “possible”. If at least one bit is not equal to one, then the set of this element does not contain - the answer is “no”, the element is filtered.
')
Implementation
JavaScript code, simply because on Habré it is understandable to many. First of all, we need to somehow represent the bitmap:
function Bits() { var bits = []; function test(index) { return (bits[Math.floor(index / 32)] >>> (index % 32)) & 1; } function set(index) { bits[Math.floor(index / 32)] |= 1 << (index % 32); } return {test: test, set: set}; } Also, we need a parameterized family of hash functions to make it easier to create
k different ones. The implementation is simple, but it works surprisingly well: function Hash() { var seed = Math.floor(Math.random() * 32) + 32; return function (string) { var result = 1; for (var i = 0; i < string.length; ++i) result = (seed * result + string.charCodeAt(i)) & 0xFFFFFFFF; return result; }; } Well, actually, the Bloom filter itself:
function Bloom(size, functions) { var bits = Bits(); function add(string) { for (var i = 0; i < functions.length; ++i) bits.set(functions[i](string) % size); } function test(string) { for (var i = 0; i < functions.length; ++i) if (!bits.test(functions[i](string) % size)) return false; return true; } return {add: add, test: test}; } Example of use:
var fruits = Bloom(64, [Hash(), Hash()]); fruits.add('apple'); fruits.add('orange'); alert(fruits.test('cabbage') ? ' .' : ' , 100%.'); After the games with the parameters, it becomes clear that there must be some optimal values for them.
Optimal values
Of course, I did not deduce the theoretical optimal values myself, I just went to Wikipedia, but even without it, by turning on the logic, one can estimate and catch some regularities. For example, it makes no sense to use a large bitmap if you are going to store two values there, the opposite is also true, otherwise the array will be overcrowded, which will lead to an increase in erroneous answers “possible”. The optimal array size in bits:
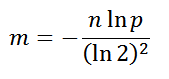
where
n is the estimated number of elements stored in the filter-set, p is the desired probability of false positives.The number of hash functions should not be large, but not small. The optimal amount:

Apply the knowledge gained:
function OptimalBloom(max_members, error_probability) { var size = -(max_members * Math.log(error_probability)) / (Math.LN2 * Math.LN2); var count = (size / max_members) * Math.LN2; size = Math.round(size); count = Math.round(count); var functions = []; for (var i = 0; i < count; ++i) functions[i] = Hash(); return Bloom(size, functions); } Where to use?
For example, Googol uses Bloom filters in its BigTable to reduce disk accesses. It is not surprising, because in fact, BigTable is a large, very sparse multidimensional table, so most of the keys point to emptiness. In addition, the data is sawn into relatively small block files, each of which is queried for requests, although it may not contain the required data.
In this case, it is advantageous to spend some RAM and greatly reduce disk usage. For example, to reduce the load by 10 times, you need to store about 5 bits of information for each key. To reduce 100 times, you need about 10 bits per key. Draw your own conclusions.
Different thoughts
Judging by the tests, the optimal values of the parameters for the practice are somewhat overestimated; we can safely lower the false response threshold by an order of two. Just be sure to test it if you use it - maybe some kind of unique combination of data and hash functions came up in my tests, or I just made a mistake somewhere.
Obviously, it is impossible to remove elements from the filter, but this is simply solved - it is enough to replace the bit array with an array of counters - increment when adding, decrement when deleting. Memory consumption naturally increases.
It is also obvious that it is impossible to dynamically change the filter parameters. The problem is elegantly solved by the introduction of a hierarchy of filters, each subsequent more accurate, if necessary, the hierarchy grows deep into.
Perhaps that's all. Until.
Source: https://habr.com/ru/post/112069/
All Articles