Fibonacci numbers on Brainfuck
After reading the Brainfuck and Lucky Tickets article at the beginning of the year, I decided it was time to study Brainfuck and write something interesting on it. I did not have to think long. I decided to write my own “abnormal” implementation of Fibonacci numbers in which the user enters a unique number that determines the number of output elements of the Fibonacci series.
I was also helped by the Brainfuck website and the ASCII character table.
First, you need to make an algorithm. And here he is:
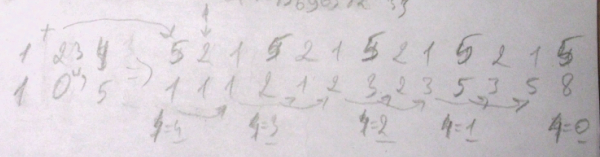
From the algorithm it can be seen that cell 1 (the top row is the cell number) at the end of each step of the cycle contains the last calculated value, and cell 2 is the last but one.
')
So let's go in order. We will decide for a start with the cells, what and where will be located. I will write in detail so that there are no complaints in the comments that there are a lot of incomprehensible points in the text of the article. And at the same time I will make a reservation that in the Fibonacci series the first two positions will be omitted and it will begin immediately from the third (0, 1, 1 , 2, 3, 5, ...).
Cell 1: Value 1
Cell 2: Value 0
Cell 3: value 32 (space)
Cell 4: input number
Cells 5 to 8: auxiliary
In cell 6 will be the total value
Further, all cells will be called Yah, where x is the sequence number of the cell.
Immediately give all the code, and then analyze it in detail. For the convenience of understanding (and writing) the code, each significant piece was written in a separate line.
(1) - here everything is elementary. In the first three lines, we fill the cells with data; in the fourth, we get the number of characters to output from the user.
(2) - we obtain from it the number necessary for the calculations, subtracting 48.
(3) - the beginning of the cycle output numbers.
(4) - I reset 5-8. In principle, it is enough to reset only 6.
(5) - I copy data from 1 to 5, 6 and 8. At the same time, H1 becomes empty.
(6) - I move the data from 6 to 1. Thus, in L1, R5 and R6, the data is copied from R1 to R5, i.e. we take two empty cells (final and auxiliary) and transfer data to them from the source to these cells, and then from the auxiliary to the original.
I write to R5 to calculate the next value of the Fibonacci series.
In 8, the last but one last row is stored.
(7, 8) - similarly (5, 6) I copy data from H2 to Z6, using Z7 as an auxiliary one.
(9) - I move the data from 6 to 5, summing up. The calculation of the value of the next Fibonacci number is made.
(10, 11) - I reset 2 and move the data from 8 to 2.
(12, 13) - I reset 1 and move the data from 5 to 1 and 6.
Thus, in L1 we have the last calculated value recorded, and in L2, the last but one value.
(14) - I increase the value of 6 to 48 and display the value on the screen.
(15) - I bring a space.
(16) - reduce the counter, the end of the cycle.
(17) - transition to a new line, carriage shift (output 13, 10).
The first time when I finished writing a program, I discovered that it brought me not a Fibonacci series at all, but a slightly different one, not far from the programming world. I had to take up the pencil once more and disassemble each step:

Oh, if I knew that I had counted on one more step forward, I would have found a mistake more quickly. Thus, I had to calculate the location of the error, for which the following code came in handy between (15) and (16), which displayed the contents of 1 and 2, using 7:
Then I had to poshaman a little more and, as a result, it turned out that I simply did not nullify H2 (10). It turned out that by removing the line (10), you get a number of powers of two. :)
Here, in general, that's all. The entire text of the application in brief:
Result of performance:
The main thing to remember is that in Brainfuck everything is relative to the current cell and the value in each. (:
Homework for beginners: implement the output N of the number of elements of the Fibonacci series, where N is a two-digit number.
I was also helped by the Brainfuck website and the ASCII character table.
Well, rushed!
First, you need to make an algorithm. And here he is:
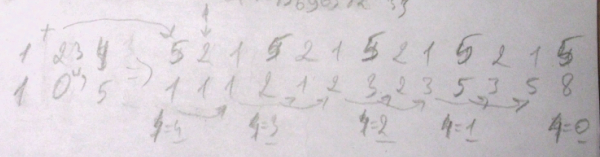
From the algorithm it can be seen that cell 1 (the top row is the cell number) at the end of each step of the cycle contains the last calculated value, and cell 2 is the last but one.
')
So let's go in order. We will decide for a start with the cells, what and where will be located. I will write in detail so that there are no complaints in the comments that there are a lot of incomprehensible points in the text of the article. And at the same time I will make a reservation that in the Fibonacci series the first two positions will be omitted and it will begin immediately from the third (0, 1, 1 , 2, 3, 5, ...).
Cell 1: Value 1
Cell 2: Value 0
Cell 3: value 32 (space)
Cell 4: input number
Cells 5 to 8: auxiliary
In cell 6 will be the total value
Further, all cells will be called Yah, where x is the sequence number of the cell.
Immediately give all the code, and then analyze it in detail. For the convenience of understanding (and writing) the code, each significant piece was written in a separate line.
+ (1)
>
>++++++++++ ++++++++++ ++++++++++ ++
>,
>++++++++[<------>-] (2)
<[ (3)
>[-]>[-]>[-]>[-] (4)
<<<<<<<[>>>>+>+>>+<<<<<<<-] (5)
>>>>>[<<<<<+>>>>>-] (6)
<<<<[>>>>+>+<<<<<-] (7)
>>>>>[<<<<<+>>>>>-] (8)
<[<+>-] (9)
<<<<[-] (10)
>>>>>>[<<<<<<+>>>>>>-] (11)
<<<<<<<[-] (12)
>>>>[<<<<+>>>>>+<-] (13)
++++++++[>++++++<-]>. (14)
<<<. (15)
>-] (16)
+++++++++++++.---. (17)
Let's start the analysis of the code.
(1) - here everything is elementary. In the first three lines, we fill the cells with data; in the fourth, we get the number of characters to output from the user.
(2) - we obtain from it the number necessary for the calculations, subtracting 48.
(3) - the beginning of the cycle output numbers.
(4) - I reset 5-8. In principle, it is enough to reset only 6.
(5) - I copy data from 1 to 5, 6 and 8. At the same time, H1 becomes empty.
(6) - I move the data from 6 to 1. Thus, in L1, R5 and R6, the data is copied from R1 to R5, i.e. we take two empty cells (final and auxiliary) and transfer data to them from the source to these cells, and then from the auxiliary to the original.
I write to R5 to calculate the next value of the Fibonacci series.
In 8, the last but one last row is stored.
(7, 8) - similarly (5, 6) I copy data from H2 to Z6, using Z7 as an auxiliary one.
(9) - I move the data from 6 to 5, summing up. The calculation of the value of the next Fibonacci number is made.
(10, 11) - I reset 2 and move the data from 8 to 2.
(12, 13) - I reset 1 and move the data from 5 to 1 and 6.
Thus, in L1 we have the last calculated value recorded, and in L2, the last but one value.
(14) - I increase the value of 6 to 48 and display the value on the screen.
(15) - I bring a space.
(16) - reduce the counter, the end of the cycle.
(17) - transition to a new line, carriage shift (output 13, 10).
Hidden, but revealed ability of the program.
The first time when I finished writing a program, I discovered that it brought me not a Fibonacci series at all, but a slightly different one, not far from the programming world. I had to take up the pencil once more and disassemble each step:

Oh, if I knew that I had counted on one more step forward, I would have found a mistake more quickly. Thus, I had to calculate the location of the error, for which the following code came in handy between (15) and (16), which displayed the contents of 1 and 2, using 7:
>>>>[-]
++++++++[<<<<<<++++++>>>>>>-]<<<<<<.>>>>>>++++++++[<<<<<<------>>>>>>-]
++++++++[<<<<<++++++>>>>>-]<<<<<.>>>>>++++++++[<<<<<------>>>>>-]
[-]+++++++++++++.---.[-]<<<<
Then I had to poshaman a little more and, as a result, it turned out that I simply did not nullify H2 (10). It turned out that by removing the line (10), you get a number of powers of two. :)
I finish the article.
Here, in general, that's all. The entire text of the application in brief:
+>>++++++++++++++++++++++++++++++++>,>++++++++[<------>-]<[>[-]>[-]>[-]>[-]<<<<<<<[>>>>+>+>>+<<<<<<<-]>>>>>[<<<<<+>>>>>-]<<<<[>>>>+>+<<<<<-]>>>>>[<<<<<+>>>>>-]<[<+>-]<<<<[-]>>>>>>[<<<<<<+>>>>>>-]<<<<<<<[-]>>>>[<<<<+>>>>>+<-]++++++++[>++++++<-]>.<<<.>-][-]+++++++++++++.---.
Result of performance:
9
1 2 3 5 8 = ER g
The main thing to remember is that in Brainfuck everything is relative to the current cell and the value in each. (:
Homework for beginners: implement the output N of the number of elements of the Fibonacci series, where N is a two-digit number.
Source: https://habr.com/ru/post/111935/
All Articles