Trie, or loaded tree
Hello, Habrahabr. Today I want to talk about such a wonderful data structure as a dictionary on a loaded tree , also known as a prefix tree , or trie .
A loaded tree is a data structure that implements an interface of an associative array, that is, it allows you to store key-value pairs. Immediately it should be said that in most cases the keys are strings, however, as keys, you can use any data types that can be represented as a sequence of bytes (that is, any).
A loaded tree differs from ordinary n-ary trees in that its nodes do not store keys. Instead of them, single-character labels are stored in the nodes, and the key that corresponds to a certain node is the path from the root of the tree to this node, or rather the line composed of the labels of the nodes that met along this path. In this case, the root of the tree, obviously, corresponds to the empty key.
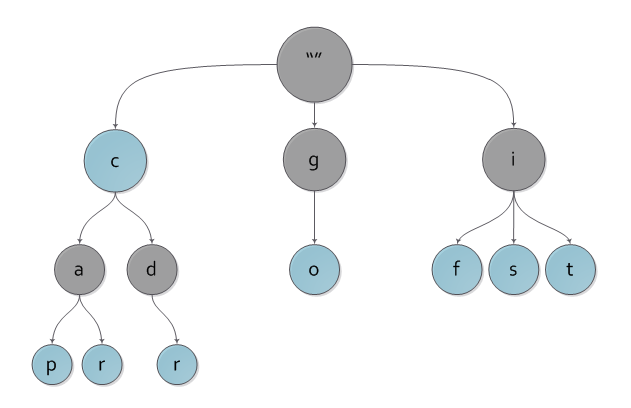
In the picture you can see an example of a loaded tree with the keys c, cap, car, cdr, go, if, is, it .
And the same tree with the car key highlighted on it.
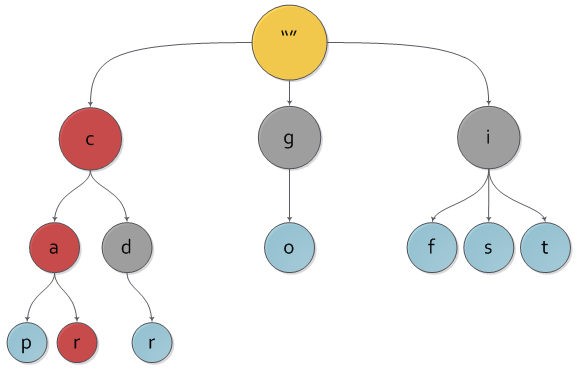
It is immediately obvious that our tree contains “extra” keys, because the only path to it from the root corresponds to any node of the tree, and therefore some key. To avoid problems with “redundant” keys, a boolean characteristic is added to each node of the tree, indicating whether the node is real or intermediate along the road to another one.
')
Since a loaded tree implements an interface of an associative array, three basic operations can be distinguished in it, namely, insertion, deletion, and key search. Like many trees, a loaded tree has the property of self-similarity, that is, any of its subtrees are also full-fledged loaded trees. It is easy to see that all the keys in such a subtree have a common prefix, (whence the name “prefix tree” came from), which means you can select a specific operation for this tree - getting all the keys of a tree with a given prefix during O (| Prefix |).
As already mentioned, the key corresponding to a node is the concatenation of labels of the nodes contained in the path from the root to the given node. From this property, the key search algorithm naturally follows (as, incidentally, the add and remove algorithms).
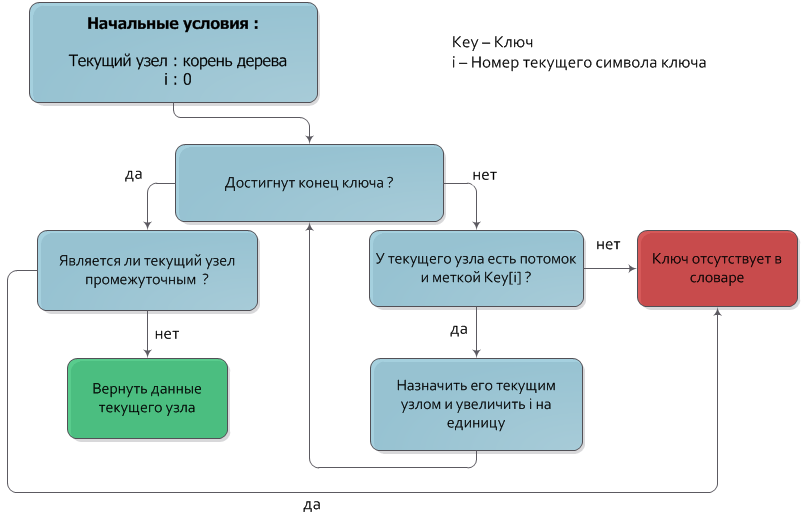
Let given the key Key, which must be found in the tree. We will descend from the root of the tree to the lower levels, each time moving into a node whose label coincides with the next key symbol. After all the key symbols are processed, the node in which the descent has stopped and will be the required node. If during the descent there was no node with a label corresponding to the next key symbol, or the descent stopped at an intermediate vertex (a vertex that does not matter), then the required key is not in the tree.
The time complexity of this algorithm is obviously O (| Key |).
The algorithm is shown in more detail in the flowchart:
The algorithm for adding a key to a tree is very similar to the search algorithm.
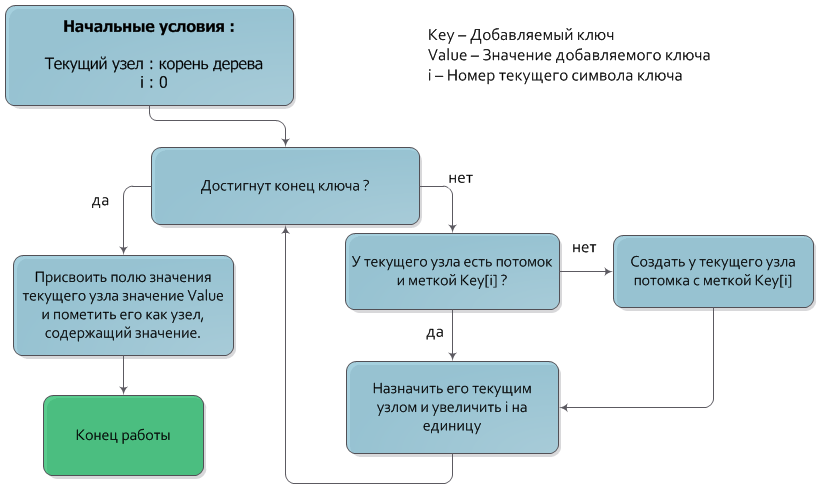
Let a pair of Key and Value values be given to be added. As in the key search algorithm, we will descend from the root of the tree to the lower levels, each time moving to a node whose label matches the next key symbol. After all the key symbols have been processed, the node where the descent has stopped will be the node to which the Value value should be assigned (also, of course, the node should be marked as having a value). If in the process of descent there is no node with a label corresponding to the next key symbol, then you should create a new intermediate node with the desired label and designate it as a child of the current one.
The time complexity of adding a key is O (| Key |).
Algorithm illustration on the flowchart:
Deleting a key is also very easy.
Let given Key key, which must be removed from the tree. Let's search for this key. If the key exists in the dictionary, then knowing the node to which it corresponds, you can simply mark it as an intermediate one, making it “invisible” for subsequent searches.
After that, you can go up from the “disabled” node to the root, simultaneously removing all nodes that are leaves, but saving memory is not significant in this case, and to effectively determine whether a node is a sheet, you need to enter an additional characteristic of the node.
The temporal estimation of the deletion algorithm is already familiar O (| Key |).
The loaded tree in terms of memory consumption / CPU time is not inferior to hash tables and balanced trees, and sometimes surpasses them in these parameters.
The complexity of the operations of insertion, deletion and search - O (| Key |). Although balanced trees perform these operations for O (ln (n)), but in this asymptotics there is a hidden time required for comparing keys, which, in general, is O (| Key |). With hash tables, the situation is similar - although the access time is O (1 + a), but taking a hash (if it is not precomputed in advance, of course) takes O (| Key |).
Graphs with a comparison of the performance of loaded trees, hash tables and red-black trees can be viewed in the English Wikipedia .
In memory consumption, a loaded tree often wins over hash tables and balanced trees. This is due to the fact that the set of keys in the loaded tree match the prefixes, and together with them the memory they use. Also, unlike balanced trees, in a loaded tree there is no need to store a key in each node.
There are 2 main types of optimization of a loaded tree:
Actually, the scope of loaded trees is enormous - they can be used everywhere where the implementation of an associative array interface is required. Especially loaded trees are convenient for the implementation of dictionaries, spellcheckers and other T9 - that is, in tasks where you need to quickly receive sets of keys with a given prefix. Also, the loaded tree uses in its work the well-known algorithm of Aho - Korasik .
That's all. I hope the reader was interested to learn about this wonderful data structure, unfairly rarely mentioned in Habré.
What is it ?
A loaded tree is a data structure that implements an interface of an associative array, that is, it allows you to store key-value pairs. Immediately it should be said that in most cases the keys are strings, however, as keys, you can use any data types that can be represented as a sequence of bytes (that is, any).
How it works ?
A loaded tree differs from ordinary n-ary trees in that its nodes do not store keys. Instead of them, single-character labels are stored in the nodes, and the key that corresponds to a certain node is the path from the root of the tree to this node, or rather the line composed of the labels of the nodes that met along this path. In this case, the root of the tree, obviously, corresponds to the empty key.
In the picture you can see an example of a loaded tree with the keys c, cap, car, cdr, go, if, is, it .

And the same tree with the car key highlighted on it.

It is immediately obvious that our tree contains “extra” keys, because the only path to it from the root corresponds to any node of the tree, and therefore some key. To avoid problems with “redundant” keys, a boolean characteristic is added to each node of the tree, indicating whether the node is real or intermediate along the road to another one.
')
Basic operations
Since a loaded tree implements an interface of an associative array, three basic operations can be distinguished in it, namely, insertion, deletion, and key search. Like many trees, a loaded tree has the property of self-similarity, that is, any of its subtrees are also full-fledged loaded trees. It is easy to see that all the keys in such a subtree have a common prefix, (whence the name “prefix tree” came from), which means you can select a specific operation for this tree - getting all the keys of a tree with a given prefix during O (| Prefix |).
Key search
As already mentioned, the key corresponding to a node is the concatenation of labels of the nodes contained in the path from the root to the given node. From this property, the key search algorithm naturally follows (as, incidentally, the add and remove algorithms).
Let given the key Key, which must be found in the tree. We will descend from the root of the tree to the lower levels, each time moving into a node whose label coincides with the next key symbol. After all the key symbols are processed, the node in which the descent has stopped and will be the required node. If during the descent there was no node with a label corresponding to the next key symbol, or the descent stopped at an intermediate vertex (a vertex that does not matter), then the required key is not in the tree.
The time complexity of this algorithm is obviously O (| Key |).
The algorithm is shown in more detail in the flowchart:

Insert
The algorithm for adding a key to a tree is very similar to the search algorithm.
Let a pair of Key and Value values be given to be added. As in the key search algorithm, we will descend from the root of the tree to the lower levels, each time moving to a node whose label matches the next key symbol. After all the key symbols have been processed, the node where the descent has stopped will be the node to which the Value value should be assigned (also, of course, the node should be marked as having a value). If in the process of descent there is no node with a label corresponding to the next key symbol, then you should create a new intermediate node with the desired label and designate it as a child of the current one.
The time complexity of adding a key is O (| Key |).
Algorithm illustration on the flowchart:

Deletion
Deleting a key is also very easy.
Let given Key key, which must be removed from the tree. Let's search for this key. If the key exists in the dictionary, then knowing the node to which it corresponds, you can simply mark it as an intermediate one, making it “invisible” for subsequent searches.
After that, you can go up from the “disabled” node to the root, simultaneously removing all nodes that are leaves, but saving memory is not significant in this case, and to effectively determine whether a node is a sheet, you need to enter an additional characteristic of the node.
The temporal estimation of the deletion algorithm is already familiar O (| Key |).
Resource requirements
The loaded tree in terms of memory consumption / CPU time is not inferior to hash tables and balanced trees, and sometimes surpasses them in these parameters.
CPU time
The complexity of the operations of insertion, deletion and search - O (| Key |). Although balanced trees perform these operations for O (ln (n)), but in this asymptotics there is a hidden time required for comparing keys, which, in general, is O (| Key |). With hash tables, the situation is similar - although the access time is O (1 + a), but taking a hash (if it is not precomputed in advance, of course) takes O (| Key |).
Graphs with a comparison of the performance of loaded trees, hash tables and red-black trees can be viewed in the English Wikipedia .
Memory
In memory consumption, a loaded tree often wins over hash tables and balanced trees. This is due to the fact that the set of keys in the loaded tree match the prefixes, and together with them the memory they use. Also, unlike balanced trees, in a loaded tree there is no need to store a key in each node.
Optimization
There are 2 main types of optimization of a loaded tree:
- Compression . A compressed loaded tree is obtained from the usual removal of intermediate nodes, which lead to a single non-intermediate node. For example, a chain of intermediate nodes labeled a, b, c is replaced with one node labeled abc .
- Patricia . Patricia loaded tree is obtained from compressed (or ordinary) removal of intermediate nodes that have one child.
Why is all this necessary?
Actually, the scope of loaded trees is enormous - they can be used everywhere where the implementation of an associative array interface is required. Especially loaded trees are convenient for the implementation of dictionaries, spellcheckers and other T9 - that is, in tasks where you need to quickly receive sets of keys with a given prefix. Also, the loaded tree uses in its work the well-known algorithm of Aho - Korasik .
That's all. I hope the reader was interested to learn about this wonderful data structure, unfairly rarely mentioned in Habré.
Source: https://habr.com/ru/post/111874/
All Articles