The use of evolutionary strategies to identify the parameters of fuzzy systems

Essence of the work

The widespread use of fuzzy systems for solving problems of automatic control, forecasting, decision-making forces specialists to look for effective methods for building systems, to identify which, along with optimization algorithms based on derivatives, genetic algorithms, evolutionary strategies and neural networks are used. Evolutionary strategies together with evolutionary programming and a genetic algorithm represent the three main directions of evolutionary modeling. Although each method arose independently of the others, they are characterized by a number of common properties. For any of them, the initial population is formed, which is subject to selection and the influence of various genetic operators, which allows us to find better solutions. Evolutionary strategy is the algorithms created as methods for solving problem optimization and based on the principles of natural evolution. The aim of the work is to describe the classical algorithm of the evolutionary strategy for identifying a fuzzy system.

Basic concepts

A population is a finite set of individuals.
Individuals are chromosomes with a variety of parameters encoded in them.
A gene is an atomic element of a genotype (a property of a chromosome).
Genotype (structure) - a set of chromosomes of this individual
Phenotype - a set of values ​​corresponding to a given genotype (decoded structure or a set of problem parameters) - a solution, a point in the search space.
Allele - the value of a specific gene, property or variant property.
Locus (position) - indicates the location of the gene in the chromosome. And lokas are many positions of genes.
The function of fitness is a measure of the fitness of a given individual in a population.
Parameter identification is the determination of the unknown parameters of antecedents and sequential fuzzy rules by optimizing the operation of a fuzzy system according to a given criterion.
The rule base is a structure that describes the logic of the operation of the approximator / classifier and consists of rules.
Rules - Element of the base of the following rules.
For the approximation problem:
')
Ri: If x1 = A1i and x2 = A2i and x3 = A3i and ... and ... xn = Ani then y =
where x = (x1, x2, x3, ..., xn) is the vector of parameters of the approximated model;
Aki is a fuzzy term characterizing the k-th parameter in the i-th rule;
Ψ is the numerical value of the output of the approximator.

The approximator is a computational block, at the input of which the values ​​of model parameters arrive and it is required to obtain a number that will be close in the model.
Antecedent is the part of the rule for the approximation problem, which corresponds to the part of the rule up to the keyword then ...
The consicvent is the part of the rule for the approximation problem, corresponding to the part of the rule after the then keyword. [one]

Fuzzy system

Fuzzy modeling is carried out by means of a fuzzy inference system, which performs the following actions [2, 3]:
1. Converts numerical information into linguistic variables (fuzzification process);
2. Handles linguistic information, performing logical operations of fuzzy conjunction, implication and aggregation of rules;
3. Generates numerical results (defuzzification process).
The fuzzification process describes the domain by means of linguistic variables and natural language rules containing a qualitative assessment of the situation. The basis for describing the situation is a fuzzy statement of the following form:
xi is Ai or xi = Ai,

where xi is a quantity; Ai is an element of a term set of a linguistic variable from the subject area under study.
Linguistic information is processed using the rule base. Each rule consists of two parts: conditional and final. Antecedent or conditional part (IF-part) contains a statement regarding the values ​​of the input variables, the value of the output variable is specified in the sequential or final part (TO-part). Thus, a fuzzy system like “many inputs - one output” can be defined by fuzzy rules of the following form:

rule 1: IF x1 = 11 And x2 = 21 And ... And xm = Am1 THAT r = R1;
rule 2: IF x1 = 12 And x2 = 22 And ... And xm = Am2 THAT r = R2;
…………………………………………………………………………………… ..….…. ……
rule n: IF x1 = A1n And x2 = A2n And ... And xm = mn TO r = Rn,

where x1, x2, ..., xm are input variables;
r is the output variable;
ij - fuzzy areas of definition of input variables, which are defined on the universal sets X1, X2, ..., Xm;
Rs is the value of the output variable, which can be represented as a real number, or as a function defined on the input variables, or as a fuzzy domain of the output variable. Each fuzzy area ij is associated with the membership function 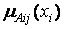[four].
The defuzzification process depends on the type of fuzzy system.
Consider a fuzzy singleton model. It is defined by the rules of the form:
rule i:

IF x1 = A1i And x2 = A2i And ... And xm = Am TO r = ai,

where ai is a real number.

Model type singleton performs mapping , replacing the fuzzy conjunction operator with the product, and the aggregation operator of fuzzy rules - with addition. The mapping F is defined by the following formula:
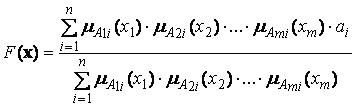, (1.1)
Where ,
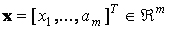n is the number of fuzzy model rules;
m is the number of input variables in the model;
- the membership function of a fuzzy area.

Membership function

The membership functions for fuzzy systems are a subjective view of the domain expert. Often this subjectivity helps to reduce the degree of uncertainty in solving weakly formalized problems. As a rule, to define membership functions, typical dependencies are used, the parameters of which are determined by processing expert opinions. Representation of arbitrary functions in the implementation of automated systems is often difficult, so in real development such dependencies are approximated by piecewise linear functions [5].
The output of a fuzzy model directly depends on the type of the membership function, for example, using triangular functions, we get:
(1.2)

Parametric identification

The parameters of the membership function of input variables of a fuzzy system can be represented as follows:

Xromosoma = [N_xromosomi, N_ruls, N_peremennoi, [an, bn, cn]] (1.3)

where N_xromosomi is the number of the generated chromosome;
N_ruls - rule number;
N_peremennoi - variable number;
[an, bn, cn] is a triple of parameters in a singleton type model with triangular membership functions.

The parameters included in this vector affect the adequacy of the model. The task of parametric identification is to determine the unknown parameters of sequential fuzzy rules by optimizing the operation of a fuzzy system according to a given criterion.
Parametric identification is considered as a process of optimizing a fuzzy model, which is reduced to finding such parameters of a fuzzy system so that the output error is minimal.
At the same time, the quality of fuzzy inference is estimated from the output error values ​​(- differences between the output variable values ​​from the observation table f (x) and the F (x) values ​​obtained by the fuzzy system. Three types of output error are investigated:
RMS error:
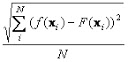(1.4)
Average Absolute Error:
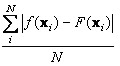(1.5)
Maximum error:
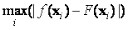(1.6)

Output errors are in the following form:

Error_for_xromosoma = [N_xromosomi, N_type_error] (1.7)

where N_xromosomi is the chromosome number,
N_type_error-type error.

For the tasks of parametric identification of a fuzzy system, the algorithm of the evolutionary strategy is adapted [1].

Evolutionary strategy

Evolutionary strategy is a heuristic optimization method in the section of evolutionary algorithms based on adaptation and evolution. The strategy is based on the mechanisms of natural selection and inheritance. It uses the principle of survival of the fittest individuals. The advantages of the algorithm over other optimization methods are in parallel processing of a variety of alternative solutions. [3]
The algorithm works with a population of individuals (chromosomes), each of which is an ordered set of task parameters to be optimized. The main characteristic of each individual is its measure of fitness.
When searching for a solution in an evolutionary strategy, mutation and crossing of individuals first occur to produce offspring, then deterministic selection occurs without repeating the best individuals from the general generation of parents and offspring. As a mutation, the addition of a normally distributed random variable to each component of the chromosome is often used. In this case, the parameters of the normal distribution are self-adapted during the execution of the algorithm.
The operation of the algorithm is an iterative process that continues until one of the stopping conditions is met:
• implementation of a specified number of generations;
• termination of population improvement.

An evolutionary strategy algorithm for tuning a fuzzy system

The classic evolutionary strategy algorithm for tuning a fuzzy system is shown below:
Entrance:
Table of observations;
Output:
Optimized rule base. The value of the fuzzy inference error.

Algorithm:
Step 1. Setting the number of terms
Step 2. Building a rule base for each chromosome:
• Construction of fuzzy terms evenly distributed over each variable
• Setting sequential for each rule using the closest observation from the table
Step 3. Generation of chromosomes
Step 4. Counting errors
Step 5. Selecting the parameters of the evolutionary strategy algorithm:
• setting the number of iterations
• number of crossing points and crossing algorithm
• probability of mutation
• type of selection algorithm
Step 6. Generation of the initial population
Step 7. Calculate fitness measure.
If the exit condition is reached Step 11, otherwise Step 8
Step 8. Apply the crossing algorithm
Step 9. Apply mutation algorithm
Step 10. Selection and selection of chromosomes for the new population. Go to Step 7
Step 11. Finding the solution - the “best” chromosome

Algorithmic part of the program

In the visual programming environment Microsoft Visual Studio 2010, a program was written for parametric identification of fuzzy systems, which is based on an evolutionary strategy algorithm.
The input data is the table of observations, the output is a set of parameters of a fuzzy system, which provides the most adequate construction of the model, and the values ​​of the basic errors by which the adequacy is assessed.
Implemented several types of cross operator: multipoint and unified type. Selection - random selection, tournament selection, roulette selection and elitism strategy. As a result of the use of the mutation operator, changes are randomly made in the genes of some individuals. Multipoint random mutations were investigated.

Conclusion

During the development and research of the parametric identification system of fuzzy models, test results were obtained on test functions, which showed the need for refinement and possible upgrades.
In the future we plan to test the system for real data, comparing the results with the methods of the genetic algorithm. Modernization of the evolutionary strategy due to the use of covariance matrices. It is also possible to use other membership functions. But more about that next time.

Literature

1. S. Hoche, and S. Wrobel. Evolution Strategies for Multirelational Boosting. Proc. 13th int. Conf. on ILP 2003.
2. Espinosa J., Vandewalle J., Wertz V. Fuzzy logic, identification and predictive control. - London: Springer-Verlag, 2005. - 263 p.
3. Rutkovskaya D., Pilinsky M., Rutkovsky L.: Neural networks, genetic algorithms and fuzzy systems. - M .: Hotline Telecom, 2006. - 452 p.
4. Khodashinsky I.A. Identification technology of fuzzy models such as singleton and Mamdani. / Proceedings of the VII International Conference "System Identification and Control Problems" SICPRO '08. Moscow, January 28-31, 2008. Institute of Management Problems. V.A. Trapeznikova RAS. - M: Institute of Management Problems. V.A. Trapeznikova RAS, 2008. - p. 137-163.
5. Korneev V.V., Gareev A.F., Vasyutin S.V., Raikh V.V. Database. Intellectual information processing. - M .: "Knowledge", 2000. 352 p.
6. Panteleev A.V., Letova T.A. Optimization methods in examples and tasks. - M .: Higher. Shk., 2005. - 544 c

Thanks for attention!