Molecular Dynamics Programming
Good time of the day habrazhiteli and habrazhitelnitsy. Today I would like to share with you my attempts in programming physical processes. More specifically, an attempt to go deeper to molecular scales. The topic of conversation under habrakatom - molecular dynamics.
As Wikipedia says, MD is a method in which the temporal evolution of a system of interacting atoms or particles is monitored by integrating their equations of motion.
If it is even simpler, we set the initial conditions (velocities, positions of particles, their type) and knowing the laws of their interaction, we see what happens from this. It reminds me of the good old game Live.
It's all very simple. The interactions between particles (in my particular case, the atoms) will be considered using classical physics:

This, at first glance, tangled formula - in fact, a complete analogue of the school F = ma.
(in fact, the “tangled” formula is longer, and it looks less aesthetically pleasing - I deliberately forgot the dissipative component)
Mathematically, particle modeling is the solution to the Cauchy problem for the equations above.
Calculating the whole thing, I commissioned the Verlet algorithm.
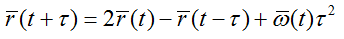
IMHO, it is optimal in accuracy and speed. But one thing - he needs to know the two previous positions of the particle! Therefore, we leave the first step to the inaccurate Euler.
')
F (r) in the formula above, is determined by the potential. In general, the potential here is the king and god - it is his influence the most significant. I chose a rather popular one - meet Lennard-Jones:
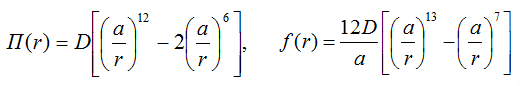
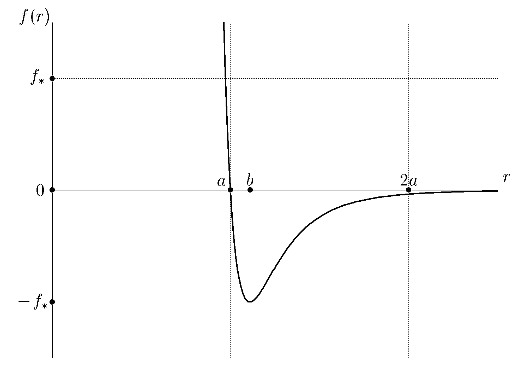
And this is how it looks, here is the interatomic distance, f is the interaction force, r is the distance between particles.
Let's move on to programming. Having scored all this in the code, we get arrays of accelerations and coordinates at the output (oh yeah, the verle does not operate with speeds, speeds can be obtained, for example, with the help of central differences). I commissioned OpenGL to render all this stuffing, especially without bothering.
Let's look at the splitting strike (1083 particles, the drummer "falls" on the target)





Exactly this moment, perhaps the most enjoyable - to play with a fresh model. Only the low calculation speed was depressing - it was time for optimizations.
First of all, I had to go back to physics. Only one glance at the potential made it clear - with a radius greater than 2a - it is possible not to count. Those. the easiest way is for each particle to consider the interaction only with particles falling into a sphere of radius a2 with the center in the particle for which we consider. One condition is “if” and the calculation is accelerated by several times (depending on the number of particles and the region).
Watching the full load of one core on my inpatient is a dull exercise. It's time to parallelize the process. Moreover, it is MD perfectly paralleled. It would seem that everything is simple - set the correspondence: a particle is a processor and count. Practice has shown that it is better to parallelize, breaking space into a grid, and here's why.
Having created a grid with a cell size equal to a, we kill two birds with one stone - we solve the problem with the calculation area, where interaction is taken into account and we make the exchange between processors more transparent and simple. Here is how it looks on the example of two processors:

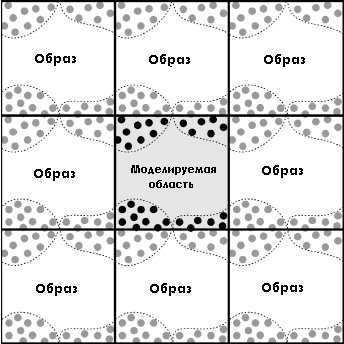
Here it is worth mentioning that any model is “chased” by various “hacks” depending on the initial conditions. For example, if we need to model something infinite (or huge) with the same structure in one or several directions, periodic boundary conditions can be applied. I applied this to simulate the friction of two endless surfaces.
The point here is that its “images” are built around the computational domain, with the current position of the particles. And the particles of the "real" area interact with the particles in the "image". And if the particle crosses the boundary of the computational domain, it appears on the other side (aka tunnel in pakmana). Below is an example of periodic conditions for x and y.
But to simulate friction, I used periodicals on only one axis:




It turned out quite an interesting and visual model, which is quite possible both to play and try to use it for real calculation (the accuracy of the results is very decent). For a good application, it would be worth sharpening under Cuda or OpenCL - the speed of calculating the MD on video cards, with proper parallelization, is simply beyond the limit! However, relying on his laziness - soon it is unlikely to happen.
PS: For the most part, I relied only on one book: The particle method and its use in the mechanics of a deformable solid matter. Krivtsov A.M., Krivtsova N.V.
What is MD?
As Wikipedia says, MD is a method in which the temporal evolution of a system of interacting atoms or particles is monitored by integrating their equations of motion.
If it is even simpler, we set the initial conditions (velocities, positions of particles, their type) and knowing the laws of their interaction, we see what happens from this. It reminds me of the good old game Live.
Maths
It's all very simple. The interactions between particles (in my particular case, the atoms) will be considered using classical physics:

This, at first glance, tangled formula - in fact, a complete analogue of the school F = ma.
(in fact, the “tangled” formula is longer, and it looks less aesthetically pleasing - I deliberately forgot the dissipative component)
Mathematically, particle modeling is the solution to the Cauchy problem for the equations above.
Calculating the whole thing, I commissioned the Verlet algorithm.
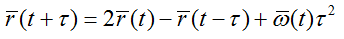
IMHO, it is optimal in accuracy and speed. But one thing - he needs to know the two previous positions of the particle! Therefore, we leave the first step to the inaccurate Euler.
')
Without potential anywhere
F (r) in the formula above, is determined by the potential. In general, the potential here is the king and god - it is his influence the most significant. I chose a rather popular one - meet Lennard-Jones:
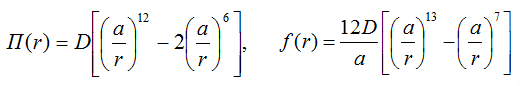
And this is how it looks, here is the interatomic distance, f is the interaction force, r is the distance between particles.

Enough formulas
Let's move on to programming. Having scored all this in the code, we get arrays of accelerations and coordinates at the output (oh yeah, the verle does not operate with speeds, speeds can be obtained, for example, with the help of central differences). I commissioned OpenGL to render all this stuffing, especially without bothering.
Let's look at the splitting strike (1083 particles, the drummer "falls" on the target)





Exactly this moment, perhaps the most enjoyable - to play with a fresh model. Only the low calculation speed was depressing - it was time for optimizations.
Accelerate
First of all, I had to go back to physics. Only one glance at the potential made it clear - with a radius greater than 2a - it is possible not to count. Those. the easiest way is for each particle to consider the interaction only with particles falling into a sphere of radius a2 with the center in the particle for which we consider. One condition is “if” and the calculation is accelerated by several times (depending on the number of particles and the region).
Watching the full load of one core on my inpatient is a dull exercise. It's time to parallelize the process. Moreover, it is MD perfectly paralleled. It would seem that everything is simple - set the correspondence: a particle is a processor and count. Practice has shown that it is better to parallelize, breaking space into a grid, and here's why.
Having created a grid with a cell size equal to a, we kill two birds with one stone - we solve the problem with the calculation area, where interaction is taken into account and we make the exchange between processors more transparent and simple. Here is how it looks on the example of two processors:

Here it is worth mentioning that any model is “chased” by various “hacks” depending on the initial conditions. For example, if we need to model something infinite (or huge) with the same structure in one or several directions, periodic boundary conditions can be applied. I applied this to simulate the friction of two endless surfaces.
The point here is that its “images” are built around the computational domain, with the current position of the particles. And the particles of the "real" area interact with the particles in the "image". And if the particle crosses the boundary of the computational domain, it appears on the other side (aka tunnel in pakmana). Below is an example of periodic conditions for x and y.

But to simulate friction, I used periodicals on only one axis:




Conclusion
It turned out quite an interesting and visual model, which is quite possible both to play and try to use it for real calculation (the accuracy of the results is very decent). For a good application, it would be worth sharpening under Cuda or OpenCL - the speed of calculating the MD on video cards, with proper parallelization, is simply beyond the limit! However, relying on his laziness - soon it is unlikely to happen.
PS: For the most part, I relied only on one book: The particle method and its use in the mechanics of a deformable solid matter. Krivtsov A.M., Krivtsova N.V.
Source: https://habr.com/ru/post/111413/
All Articles