Bicubic interpolation, theory and practical implementation
There was a task to visualize the results of some measurements on a 2-dimensional map, the results were known at the nodal points on a uniform grid, respectively, the task was reduced to interpolating the obtained data. The main requirement was the quality of the resulting image and the minimum number of interpolation artifacts, so the choice fell on the bicubic interpolation. The articles in Wiki seemed to me dry (at least for a person who did not study mathematics from school), but there was also a link to an amazing article describing the algorithm in detail. Here we look at the practical application of this algorithm and analyze the article.
(c) Wiki
To better understand the principle of bicubic interpolation, I propose to consider the principle of cubic interpolation.
')
If the values of the function f (x) and its derivative are known at the points x = 0 and x = 1, then the function can be interpolated on the interval [0, 1] using a third-order polynomial. The formula for the calculation can be easily obtained.
Third-order polynomial and its derivative:
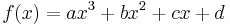
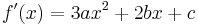
The values of the polynomial and its derivative at the points x = 0 and x = 1

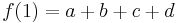
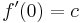
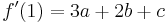
These four identities can be written as:
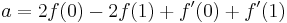
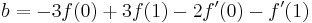

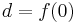
So we got our interpolation formula
In practice, the algorithm is used to interpolate a function, having certain known values at specified points. In this case, we cannot know the derivative of the function. We could take the derivative at given points as 0, but to obtain smoother and more likely function graphs, we take the slope of the line between the previous and the next point as the derivative. Thus for the calculations we need 4 points. Suppose we have 4 function values at the points p0, p1, p2 and p3, located respectively at x = -1, x = 0, x = 1 and x = 2. Substitute the obtained values of f (0), f (1), f (2) and f (3):

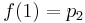
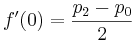

Comparing these data with the previously obtained formulas, we have:
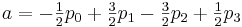
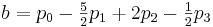
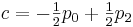
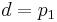
Result:

Consider the implementation of this algorithm in PHP:
Bicubic interpolation is a cubic interpolation in two dimensions. In fact, we can interpolate in more dimensions, but in this article, we consider only this example.
Imagine that we know 16 points p ij , with a point of origin in (i-1, j-1), where i, j vary from 0 to 3. Then, we can interpolate the surface in the section [0,0] x [ 1,1], for this we interpolate 4 columns and then interpolate the obtained results in the horizontal direction:
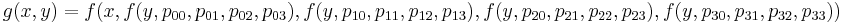
The implementation of the method in PHP, combined with the first function:
Everything would be great if not for one problem - performance. In order to interpolate even a relatively small amount of data, serious computational resources are required. To optimize performance there is the following approach.
Consider our formula in the form of a multidimensional polynomial:
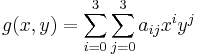
In expanded form there will be something like:
Now it is necessary to calculate the coefficients a ij . Here I would especially like to note that by calculating the coefficients once we can use them to interpolate all values in the section from [0.0] to [1.1]
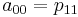
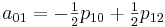
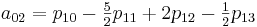


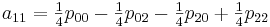


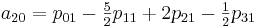
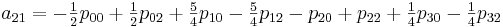


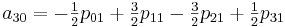



To implement this method, create the following class:
Consider the use of bicubic interpolation in the following example:
Baseline: 7 x 7 data array
Required: Imagine the surface as an image of 300 x 300 pixels.
In the code I tried to comment on every step as much as possible, I think everything will be clear
Separately made a file to create a color map

Terminology
Interpolation, interpolation - in computational mathematics, a method of finding intermediate values of a value over an existing discrete set of known values.
(c) Wiki
Cubic interpolation
To better understand the principle of bicubic interpolation, I propose to consider the principle of cubic interpolation.
')
If the values of the function f (x) and its derivative are known at the points x = 0 and x = 1, then the function can be interpolated on the interval [0, 1] using a third-order polynomial. The formula for the calculation can be easily obtained.
Third-order polynomial and its derivative:
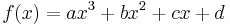
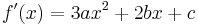
The values of the polynomial and its derivative at the points x = 0 and x = 1

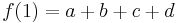
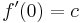
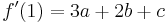
These four identities can be written as:
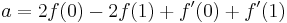
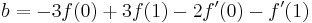

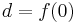
So we got our interpolation formula
In practice, the algorithm is used to interpolate a function, having certain known values at specified points. In this case, we cannot know the derivative of the function. We could take the derivative at given points as 0, but to obtain smoother and more likely function graphs, we take the slope of the line between the previous and the next point as the derivative. Thus for the calculations we need 4 points. Suppose we have 4 function values at the points p0, p1, p2 and p3, located respectively at x = -1, x = 0, x = 1 and x = 2. Substitute the obtained values of f (0), f (1), f (2) and f (3):

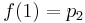
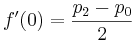

Comparing these data with the previously obtained formulas, we have:
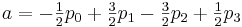
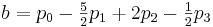
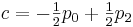
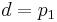
Result:

Consider the implementation of this algorithm in PHP:
/** * * * @param array $p : f(x0), f(x1), f(x2), f(x3) * @param float $x x- * @return float f($x) */ function cubicInterpolate ($p, $x) { return $p[1] + (-0.5 * $p[0] + 0.5 * $p[2]) * $x + ($p[0] - 2.5 * $p[1] + 2.0 * $p[2] - 0.5 * $p[3]) * $x * $x + (-0.5 * $p[0] + 1.5 * $p[1] - 1.5 * $p[2] + 0.5 * $p[3]) * $x * $x * $x; } Bicubic interpolation
Bicubic interpolation is a cubic interpolation in two dimensions. In fact, we can interpolate in more dimensions, but in this article, we consider only this example.
Imagine that we know 16 points p ij , with a point of origin in (i-1, j-1), where i, j vary from 0 to 3. Then, we can interpolate the surface in the section [0,0] x [ 1,1], for this we interpolate 4 columns and then interpolate the obtained results in the horizontal direction:
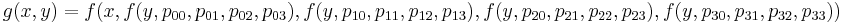
The implementation of the method in PHP, combined with the first function:
/** * * * @param array $p 2- (4 x 4), 16- * @param float $x x- * @param float $y y- * @return float f($x, $y) */ function bicubicInterpolate ($p, $x, $y) { $tmp = array(); $tmp[0] = cubicInterpolate($p[0], $y); $tmp[1] = cubicInterpolate($p[1], $y); $tmp[2] = cubicInterpolate($p[2], $y); $tmp[3] = cubicInterpolate($p[3], $y); return cubicInterpolate($tmp, $x); } Everything would be great if not for one problem - performance. In order to interpolate even a relatively small amount of data, serious computational resources are required. To optimize performance there is the following approach.
Consider our formula in the form of a multidimensional polynomial:
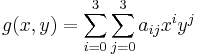
In expanded form there will be something like:
g (x, y) = a00 * x ^ 0 * y ^ 0 + a01 * x ^ 0 * y ^ 1 +
a02 * x ^ 0 * y ^ 2 + a03 * x ^ 0 * y ^ 3 +
a10 * x ^ 1 * y ^ 0 + a11 * x ^ 1 * y ^ 1 +
a12 * x ^ 1 * y ^ 2 + a13 * x ^ 1 * y ^ 3 +
a20 * x ^ 2 * y ^ 0 + a21 * x ^ 2 * y ^ 1 +
a22 * x ^ 3 * y ^ 2 + a23 * x ^ 2 * y ^ 3 +
a30 * x ^ 3 * y ^ 0 + a31 * x ^ 3 * y ^ 1 +
a32 * x ^ 3 * y ^ 2 + a33 * x ^ 3 * y ^ 3
Now it is necessary to calculate the coefficients a ij . Here I would especially like to note that by calculating the coefficients once we can use them to interpolate all values in the section from [0.0] to [1.1]
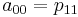
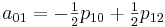
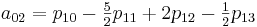


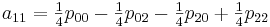


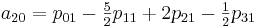
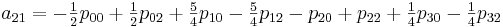


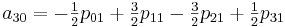



To implement this method, create the following class:
class CachedBicubicInterpolator { private $a00, $a01, $a02, $a03, $a10, $a11, $a12, $a13, $a20, $a21, $a22, $a23, $a30, $a31, $a32, $a33; /** * . * * @param array $p 2- (4 x 4), * @return void */ public function updateCoefficients ($p) { $this->a00 = $p[1][1]; $this->a01 = -.5 * $p[1][0] + .5 * $p[1][2]; $this->a02 = $p[1][0] - 2.5 * $p[1][1] + 2 * $p[1][2] - .5 * $p[1][3]; $this->a03 = -.5 * $p[1][0] + 1.5 * $p[1][1] - 1.5 * $p[1][2] + .5 * $p[1][3]; $this->a10 = -.5 * $p[0][1] + .5 * $p[2][1]; $this->a11 = .25 * $p[0][0] - .25 * $p[0][2] - .25 * $p[2][0] + .25 * $p[2][2]; $this->a12 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3] + .5 * $p[2][0] - 1.25 * $p[2][1] + $p[2][2] - .25 * $p[2][3]; $this->a13 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3] - .25 * $p[2][0] + .75 * $p[2][1] - .75 * $p[2][2] + .25 * $p[2][3]; $this->a20 = $p[0][1] - 2.5 * $p[1][1] + 2 * $p[2][1] - .5 * $p[3][1]; $this->a21 = -.5 * $p[0][0] + .5 * $p[0][2] + 1.25 * $p[1][0] - 1.25 * $p[1][2] - $p[2][0] + $p[2][2] + .25 * $p[3][0] - .25 * $p[3][2]; $this->a22 = $p[0][0] - 2.5 * $p[0][1] + 2 * $p[0][2] - .5 * $p[0][3] - 2.5 * $p[1][0] + 6.25 * $p[1][1] - 5 * $p[1][2] + 1.25 * $p[1][3] + 2 * $p[2][0] - 5 * $p[2][1] + 4 * $p[2][2] - $p[2][3] - .5 * $p[3][0] + 1.25 * $p[3][1] - $p[3][2] + .25 * $p[3][3]; $this->a23 = -.5 * $p[0][0] + 1.5 * $p[0][1] - 1.5 * $p[0][2] + .5 * $p[0][3] + 1.25 * $p[1][0] - 3.75 * $p[1][1] + 3.75 * $p[1][2] - 1.25 * $p[1][3] - $p[2][0] + 3 * $p[2][1] - 3 * $p[2][2] + $p[2][3] + .25 * $p[3][0] - .75 * $p[3][1] + .75 * $p[3][2] - .25 * $p[3][3]; $this->a30 = -.5 * $p[0][1] + 1.5 * $p[1][1] - 1.5 * $p[2][1] + .5 * $p[3][1]; $this->a31 = .25 * $p[0][0] - .25 * $p[0][2] - .75 * $p[1][0] + .75 * $p[1][2] + .75 * $p[2][0] - .75 * $p[2][2] - .25 * $p[3][0] + .25 * $p[3][2]; $this->a32 = -.5 * $p[0][0] + 1.25 * $p[0][1] - $p[0][2] + .25 * $p[0][3] + 1.5 * $p[1][0] - 3.75 * $p[1][1] + 3 * $p[1][2] - .75 * $p[1][3] - 1.5 * $p[2][0] + 3.75 * $p[2][1] - 3 * $p[2][2] + .75 * $p[2][3] + .5 * $p[3][0] - 1.25 * $p[3][1] + $p[3][2] - .25 * $p[3][3]; $this->a33 = .25 * $p[0][0] - .75 * $p[0][1] + .75 * $p[0][2] - .25 * $p[0][3] - .75 * $p[1][0] + 2.25 * $p[1][1] - 2.25 * $p[1][2] + .75 * $p[1][3] + .75 * $p[2][0] - 2.25 * $p[2][1] + 2.25 * $p[2][2] - .75 * $p[2][3] - .25 * $p[3][0] + .75 * $p[3][1] - .75 * $p[3][2] + .25 * $p[3][3]; } /** * . * * @param float $x $x = $x - $x0 * @param float $y $y = $y - $y0 * @return float . */ public function getValue ($x, $y) { // 2 3 . $x2 = $x * $x; $x3 = $x2 * $x; $y2 = $y * $y; $y3 = $y2 * $y; return ($this->a00 + $this->a01 * $y + $this->a02 * $y2 + $this->a03 * $y3) + ($this->a10 + $this->a11 * $y + $this->a12 * $y2 + $this->a13 * $y3) * $x + ($this->a20 + $this->a21 * $y + $this->a22 * $y2 + $this->a23 * $y3) * $x2 + ($this->a30 + $this->a31 * $y + $this->a32 * $y2 + $this->a33 * $y3) * $x3; } } Practical use
Consider the use of bicubic interpolation in the following example:
Baseline: 7 x 7 data array
Required: Imagine the surface as an image of 300 x 300 pixels.
In the code I tried to comment on every step as much as possible, I think everything will be clear
<?php header("Content-type: image/png");// include 'interpolation.php';// include 'colormap.php';// $simpleData = array( array(0, 0.1, 0.15, 0.2, 0.15, 0.1, 0), array(0, 0.1, 0.5, 1, 0.9, 0.1, 0), array(0, 0.1, 0.7, 1, 0.9, 0.1, 0), array(0, 0.1, 0.6, 0.7, 0.5, 0.1, 0), array(0, 0.2, 0.8, 0.6, 0.15, 0.08, 0.1), array(0.08, 0.2, 0.15, 0.2, 0.15, 0.1, 0.1), array(0.1, 0.8, 0.1, 0.1, 0.1, 0, 0) );// 7 7 $countX = count($simpleData[0]);// $countY = count($simpleData); $input = array(); /* * , * - */ for ($i = 0; $i < $countX; $i ++) { for ($j = 0; $j < $countY; $j ++) { $input[$i + 1][$j + 1] = $simpleData[$j][$i]; if ($i == 0) { $input[0][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i + 1];// } if ($i == ($countX - 1)) { $input[$countX + 1][$j + 1] = $simpleData[$j][$i] - $simpleData[$j][$i - 1];// } if ($j == 0) { $input[$i + 1][0] = $simpleData[$j][$i] - $simpleData[$j + 1][$i];// } if ($j == ($countY - 1)) { $input[$i + 1][$countY + 1] = $simpleData[$j][$i] - $simpleData[$j - 1][$i];// } } } /* * , . */ $input[0][0] = ($input[1][0] + $input[0][1]) / 2; $input[$countX + 1][0] = ($input[$countX][0] + $input[$countX][1]) / 2; $input[0][$countY + 1] = ($input[0][$countY] + $input[1][$countY]) / 2; $input[$countX + 1][$countY + 1] = ($input[$countX + 1][$countY] + $input[$countX][$countY]) / 2; $step = 50; // 50 $img = imagecreatetruecolor(($countX - 1) * $step, ($countY - 1) * $step);// $colormap = createColormap($img);// $b2i = new CachedBicubicInterpolator(); for ($i = 1; $i < $countX; $i ++) {// for ($j = 1; $j < $countY; $j ++) { $points = array(); $points[0][0] = $input[$i - 1][$j - 1]; $points[1][0] = $input[$i][$j - 1]; $points[2][0] = $input[$i + 1][$j - 1]; $points[3][0] = $input[$i + 2][$j - 1]; $points[0][1] = $input[$i - 1][$j]; $points[1][1] = $input[$i][$j]; $points[2][1] = $input[$i + 1][$j]; $points[3][1] = $input[$i + 2][$j]; $points[0][2] = $input[$i - 1][$j + 1]; $points[1][2] = $input[$i][$j + 1]; $points[2][2] = $input[$i + 1][$j + 1]; $points[3][2] = $input[$i + 2][$j + 1]; $points[0][3] = $input[$i - 1][$j + 2]; $points[1][3] = $input[$i][$j + 2]; $points[2][3] = $input[$i + 1][$j + 2]; $points[3][3] = $input[$i + 2][$j + 2]; $b2i->updateCoefficients($points);// for ($x = 0; $x < $step; $x ++) {// for ($y = 0; $y < $step; $y ++) { $rx = ($i - 1) * $step + $x;// $ry = ($j - 1) * $step + $y;//y $ax = $x / $step;//x - x0 $ay = $y / $step;//y - y0 $val = $b2i->getValue($ax, $ay);// $color = ceil(($val) * 1024) - 1;// if ($color < 0) $color = 0;// if ($color > 1023) $color = 1023;// imagesetpixel($img, $rx, $ry, $colormap[$color]);// } } } } imagepng($img); ?> Separately made a file to create a color map
function createColormap(&$image) { $colormap = array(); for ($i = 0; $i < 256; $i ++) { $colormap[$i] = imagecolorallocate($image, 0, $i, 255); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 256] = imagecolorallocate($image, 0, 255, 255 - $i); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 512] = imagecolorallocate($image, $i, 255, 0); } for ($i = 0; $i < 256; $i ++) { $colormap[$i + 768] = imagecolorallocate($image, 255, 255 - $i, 0); } return $colormap; } Result of work:

Source: https://habr.com/ru/post/111402/
All Articles